卷积

卷积、互相关和自相关的图示比较。运算涉及函数$f$，并假定$f$的高度是1.0，在5个不同点上的值，用在每个点下面的阴影面积来指示。$f$的对称性是卷积$g*f$和互相关$f\star g$在这个例子中相同的原因。

在泛函分析中，捲積（convolution），或译为疊積、-{褶}-積或旋積，是透過两个函数$f$和$g$生成第三个函数的一种数学算子，表徵函数$f$与经过翻转和平移的$g$的乘積函數所圍成的曲邊梯形的面積。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“滑動平均”的推廣。

定义

卷积是数学分析中一种重要的运算。设：$f(t)$和$g(t)$是实数$ℝ$上的两个可积函数，定义二者的卷积$(f*g)(t)$为如下特定形式的积分变换：

$(f*g)(t)\triangleq \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(\tau )g(t-\tau )\mathrm{d}\tau$

$(f*g)(t)$仍为可积函数，并且有着：

$(f*g)(t)\triangleq \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(t-\tau )g(\tau )d\tau =(g*f)(t)$

函数$f$和$g$，如果只支撑在$[0,\mathrm{\infty }]$之上，则积分界限可以截断为：

$(f*g)(t)=\underset{0}{\overset{t}{\int }}f(\tau )g(t-\tau )d\tau$对于$f,g:[0,\mathrm{\infty })\to ℝ$

对于两个得出复数值的Template:En-link，可以定义二者的卷积为如下形式的多重积分：

$\begin{array}{cc}(f*g)(t_1,t_2,\cdots ,t_n)& \triangleq \int \int \cdots \underset{{ℝ}^n}{\int }f({\tau }_1,{\tau }_2,\cdots ,{\tau }_n)g(t_1-{\tau }_1,t_2-{\tau }_2,\cdots ,t_n-{\tau }_n,)d{\tau }_{1}d{\tau }_2\cdots d{\tau }_n\\ & \triangleq \underset{{ℝ}^n}{\int }f(\tau )g(t-\tau )d^n\tau \end{array}$

卷积有一个通用的工程上的符号约定：

$f(t)*g(t)\triangleq \underset{(f*g)(t)}{\underbrace{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(\tau )g(t-\tau )d\tau }}$

它必须被谨慎解释以避免混淆。例如：$f(t)*g(t-t_0)$等价于$(f*g)(t-t_0)$，而$f(t-t_0)*g(t-t_0)$却实际上等价于$(f*g)(t-2t_0)$。

历史

卷积运算的最早使用出现在达朗贝尔于1754年出版的《宇宙体系的几个要点研究》中对泰勒定理的推导之中。还有Template:En-link，将$\int f(u)\cdot g(x-u)du$类型的表达式，用在他的1797年–1800年出版的著作《微分与级数论文》中。此后不久，卷积运算出现在皮埃尔-西蒙·拉普拉斯、约瑟夫·傅里叶和西梅翁·泊松等人的著作中。这个运算以前有时叫做“Faltung”（德语中的折叠）、合成乘积、叠加积分或卡森积分。

“卷积”这个术语早在1903年就出现了，然而其定义在早期使用中是相当生僻的，直到1950年代或1960年代之前都未曾广泛使用。

简介

如果$f$和$g$都是在L^p 空间$L^1({ℝ}^n)$内的勒贝格可积函数，则二者的卷积存在，并且在这种情况下$f*g$也是可积的。这是托內利定理的结论。对于在$L^1$中的函数在离散卷积下，或更一般的对于在任何群的上的卷积，这也是成立的。同样的，如果$f\in L^1({ℝ}^n)$而$g\in L^p({ℝ}^n)$，这里的$1\le p\le \mathrm{\infty }$，则$f*g\in L^p({ℝ}^n)$，并且其L^p 范数间有着不等式：

$\Vert f*g{\Vert }_p\le \Vert f{\Vert }_1\Vert g{\Vert }_p$

在$p=1$的特殊情况下，这显示出$L^1$是在卷积下的巴拿赫代数（并且如果$f$和$g$几乎处处非负则两边间等式成立）。

卷积与傅里叶变换有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，利用此一性質，能簡化傅里叶分析中的许多问题。

由卷积得到的函数$f*g$，一般要比$f$和$g$都光滑。特别当$g$为具有紧支集的光滑函数，$f$为局部可积时，它们的卷积$f*g$也是光滑函数。利用这一性质，对于任意的可积函数$f$，都可以简单地构造出一列逼近于$f$的光滑函数列$f_s$，这种方法称为函数的光滑化或正则化。

函数$f(t)$和$g(t)$的互相关$(f\star g)(\tau )$，等价于$f(-\tau )$的共轭复数$\overline{f(-\tau )}$与$g(\tau )$的卷积：

$(f\star g)(\tau )\triangleq \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\overline{f(t-\tau )}g(t)dt=\overline{f(-\tau )}*g(\tau )$

这里的$\tau$叫做移位（displacement）或滞后（lag）。

对于單位脈衝函数$\delta (t)$和某个函数$h(t)$，二者得到的捲積就是$h(t)$本身，此$h(t)$被稱為衝激響應：

$(\delta *h)(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\delta (\tau )h(t-\tau )d\tau =h(t)$

在连续时间线性非时变系统中，输出信号$y(t)$被描述为输入信号$x(t)$与冲激响应$h(t)$的卷积：

$y(t)=(x*h)(t)\triangleq \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t-\tau )\cdot h(\tau )\mathrm{d}\tau =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\tau )\cdot h(t-\tau )\mathrm{d}\tau$

两个独立的随机变量$U$和$V$，每个都有一个概率密度函数，二者之和的概率密度，是它们单独的密度函数的卷积：

$f_{U+V}(x)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{f}_U(y)f_V(x-y)dy=(f_U*f_V)(x)$

图解

已知右侧第一行图中两个函数$f(t)$和$g(t)$。 首先將兩個函數都用约束变量$\tau$來表示，并将$g(\tau )$翻转至纵轴另一侧，从而得到右侧第二行图中$f(\tau )$和$g(-\tau )$。 向函数$g(-\tau )$增加一个时间偏移量$t$，得到函数$g(-(\tau -t))=g(t-\tau )$。$t$不是常数而是自由变量，当$t$取不同值时，$g(t-\tau )$能沿着$\tau$轴“滑动”。如果$t$是正值，则$g(t-\tau )$等于$g(-\tau )$沿着$\tau$轴向右（朝向$+\mathrm{\infty }$）滑动数量$t$。如果$t$是负值，则$g(t-\tau )$等价于$g(-\tau )$向左（朝向$-\mathrm{\infty }$）滑动数量$|t|$。 讓$t$從$-\mathrm{\infty }$变化至$+\mathrm{\infty }$，当兩個函數交會時，計算交會範圍中兩個函數乘積的積分值。換句話說，在时间$t$，计算函数$f(\tau )$经过权重函数$g(t-\tau )$施以权重后其下的面积。右侧第三、第四和第五行图中，分别是$t=0$、$t=2.5$和$t=5.5$时的情况，从$t>1$时开始有交会，例如在第四行图中，$\tau =0$则$g(t-\tau )=g(2.5)$，$\tau =1.5$则$g(t-\tau )=g(1)$，对于$\tau \notin [0,1.5]$有着$f(\tau )g(t-\tau )=0$。 最後得到的波形（未包含在此圖中）就是$f$和$g$的捲積。
两个矩形脈衝波的捲積。其中函数$g$首先对$\tau =0$反射，接著平移$t$，成為$g(t-\tau )$。那么重叠部份的面积就相当于$t$处的卷积，其中橫坐標代表待变量$\tau$以及新函數$f\ast g$的自變量$t$。
矩形脈衝波和指數衰減脈衝波的捲積（後者可能出現於RC電路中），同樣地重疊部份面積就相當於$t$處的捲積。注意到因為$g$是對稱的，所以在這兩張圖中，反射並不會改變它的形狀。

周期卷积

Template:Main article Template:Multiple image 两个$T$周期的函数$h_{{}_T}(t)$和$x_{{}_T}(t)$的“周期卷积”定义为：

$\underset{t_0}{\overset{t_0+T}{\int }}{h}_{{}_T}(\tau )x_{{}_T}(t-\tau )d\tau$

这里的$t_0$是任意参数。

任何Template:En-link$s(t)$，都可以通过求函数$s(t)$的所有整数倍$P$的平移的总和，从而制作出具有周期$P$的周期函数 $s_{{}_P}(t)$，这叫做Template:En-link：

$s_{{}_P}(t)\triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}s(t+mP)=\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}s(t-mP),m\in \mathbb{Z}$

对于无周期函数$h$与$x$，其周期$T$的周期求和分别是$h_{{}_T}(t)$与$x_{{}_T}(t)$，$h$与$x$的周期卷积，可以定义为$h(t)$与$x_{{}_T}(t)$的常规卷积，或$x(t)$与$h_{{}_T}(t)$的常规卷积，二者都等价于$h_{{}_T}(t)$与$x_{{}_T}(t)$的周期积分：

$(h*x_{{}_T})(t)\triangleq \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}h(\tau )x_{{}_T}(t-\tau )d\tau =\underset{t_0}{\overset{t_0+T}{\int }}{h}_{{}_T}(\tau )x_{{}_T}(t-\tau )d\tau$

$(h*x_{{}_T})(t)=(x*h_{{}_T})(t)$

圆周卷积是周期卷积的特殊情况，其中函数$h$和$x$二者的非零部份，都限定在区间$[0,T]$之内，此时的周期求和称为“周期延拓”。$h*x_{{}_T}$中函数$x_{{}_T}$可以通过取非负余数的模除运算表达为“圆周函数”：

$x_{{}_T}(t)=x(t_{\mathrm{m}\mathrm{o}\mathrm{d}T}),t\in ℝ$

而积分的界限可以缩简至函数$h$的长度范围$[0,T]$：

$(h*x_{{}_T})(t)=\underset{0}{\overset{T}{\int }}h(\tau )x((t-\tau {)}_{\mathrm{m}\mathrm{o}\mathrm{d}T})d\tau$

离散卷积

离散卷积示意图

对于定义在整數$\mathbb{Z}$上且得出复数值的函数$f[n]$和$g[n]$，离散卷积定义为：

$(f*g)[n]\triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}f[m]g[n-m]=\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}f[n-m]g[m]$

這裡一樣把函數定義域以外的值當成零，所以可以擴展函數到所有整數上（如果本來不是的話）。两个有限序列的卷积的定义，是将这些序列扩展成在整数集合上有限支撑的函数。在这些序列是两个多项式的系数之时，这两个多项式的普通乘积的系数，就是这两个序列的卷积。这叫做序列系数的柯西乘积。

當$g[n]$的支撐集為有限長度的$\{-M,-M+1,\dots ,M-1,M\}$之时，上式會變成有限求和：

$(f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m]$

多维离散卷积

用离散二维卷积对图像进行Template:En-link处理的动画

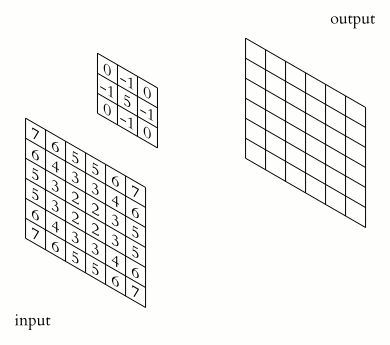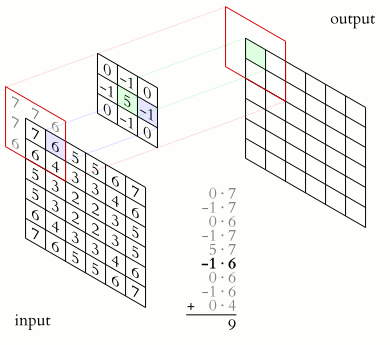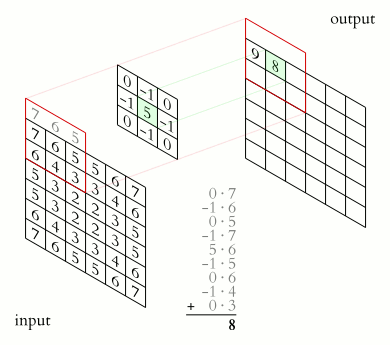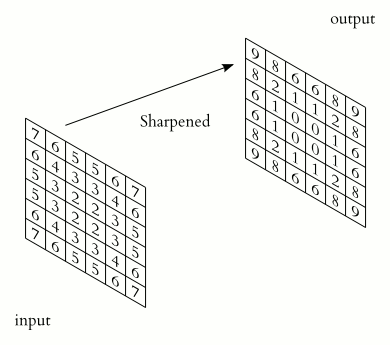
类似于一维情况，使用星号表示卷积，而维度体现在星号的数量上，$M$维卷积就写为$M$个星号。下面是$M$维信号的卷积的表示法：

$y(n_1,n_2,...,n_{{}_M})=h(n_1,n_2,...,n_{{}_M})*\stackrel{M}{\cdots }*x(n_1,n_2,...,n_{{}_M})$

对于离散值的信号，这个卷积可以直接如下这样计算：

$\sum _{k_1=-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{k_2=-\mathrm{\infty }}^{\mathrm{\infty }}...\sum _{k_{{}_M}=-\mathrm{\infty }}^{\mathrm{\infty }}h(k_1,k_2,...,k_{{}_M})x(n_1-k_1,n_2-k_2,...,n_{{}_M}-k_{{}_M})$

结果的离散多维卷积所支撑的输出区域，基于两个输入信号所支撑的大小和区域来决定。

在两个二维信号之间的卷积的可视化

离散周期卷积

对比离散无周期卷积（左列）与离散圆周卷积（右列）

对于离散序列和一个参数$N$，无周期函数$h$和$x$的“周期卷积”是为：

$(h*x_{{}_N})[n]\triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}h[m]\underset{\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}x[n-m-kN]}{\underbrace{x_{{}_N}[n-m]}}=\sum _{m=0}^{N-1}(\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}h[m-kN])x_{{}_N}[n-m]$

这个函数有周期$N$，它有最多$N$个唯一性的值。$h$和$x$的非零范围都是$[0,N-1]$的特殊情况叫做圆周卷积：

$(h*x_{{}_N})[n]=\sum _{m=0}^{N-1}h[m]x_{{}_N}[n-m]=\sum _{m=0}^{N-1}h[m]x[(n-m{)}_{modN}]$

离散圆周卷积可简约为矩阵乘法，这里的积分变换的核函数是循环矩阵:

$\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_{{}_{N-1}}\end{array}\right]=\left[\begin{array}{cccc}{h}_0& h_{{}_{N-1}}& \cdots & h_1\\ h_1& h_0& \cdots & h_2\\ ⋮& ⋮& \ddots & ⋮\\ h_{{}_{N-1}}& h_{{}_{N-2}}& \cdots & h_0\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_1\\ ⋮\\ x_{{}_{N-1}}\end{array}\right]$

圆周卷积最经常出现的快速傅里叶变换的实现算法比如雷德演算法之中。

性质

代数

Template:Main 各种卷积算子都满足下列性质：

交换律

$f*g=g*f$

结合律

$f*(g*h)=(f*g)*h$

分配律

$f*(g+h)=(f*g)+(f*h)$

数乘结合律

$a(f*g)=(af)*g=f*(ag)$

其中$a$为任意实数（或复数）。

复数共轭

$\overline{f*g}=\bar{f}*\bar{g}$

微分有关

$(f*g{)}^{\prime }=f^{\prime }*g=f*g^{\prime }$

积分有关

如果$F(t)={\int }_{-\mathrm{\infty }}^{t}f(\tau )d\tau$，并且$G(t)={\int }_{-\mathrm{\infty }}^{t}g(\tau )d\tau$，则有：

$(F*g)(t)=(f*G)(t)=\underset{-\mathrm{\infty }}{\overset{t}{\int }}(f*g)(\tau )d\tau$

积分

如果$f$和$g$是可积分函数，则它们在整个空间上的卷积的积分，简单的就是它们积分的乘积：

$\underset{{ℝ}^n}{\int }(f*g)(t)d^{n}t=(\underset{{ℝ}^n}{\int }f(t)d^{n}t)(\underset{{ℝ}^n}{\int }g(t)d^{n}t)$

这是富比尼定理的结果。如果$f$和$g$只被假定为非负可测度函数，根据托内利定理，这也是成立的。

微分

在一元函数情况下，$f$和$g$的卷积的导数有着：

$\frac{d}{dt}(f*g)=\frac{df}{dt}*g=f*\frac{dg}{dt}$

这里的$\frac{d}{dt}$是微分算子。更一般的说，在多元函数的情况下，对偏导数也有类似的公式：

$\frac{\partial }{\partial t_i}(f*g)=\frac{\partial f}{\partial t_i}*g=f*\frac{\partial g}{\partial t_i}$

这就有了一个特殊结论，卷积可以看作“光滑”运算：$f$和$g$的卷积可微分的次数，是$f$和$g$的总数。

这些恒等式成立的严格条件，为$f$和$g$是绝对可积分的，并且至少二者之一有绝对可积分（$L^1$）弱导数，这是Template:En-link的结论。

在离散情况下，差分算子$\mathrm{\Delta }[f](n)=f(n+1)-f(n)$满足类似的关系：

$\mathrm{\Delta }(f*g)=(\mathrm{\Delta }f)*g=f*(\mathrm{\Delta }g)$

卷积定理

Template:Main 卷积定理指出，在适当的条件下，两个函数（或信号）的卷积的傅里叶变换，是它们的傅里叶变换的逐点乘积。更一般的说，在一个域（比如时域）中的卷积等于在其他域（比如频域）逐点乘法。

设两个函数$g(x)$和$h(x)$，分别具有傅里叶变换$G(s)$和$H(s)$：

$\begin{array}{cc}G(s)& \triangleq ℱ\{g\}(s)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}g(x)e^{-i2\pi sx}dx,s\in ℝ\\ H(s)& \triangleq ℱ\{h\}(s)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}h(x)e^{-i2\pi sx}dx,s\in ℝ\end{array}$

这里的$ℱ$算子指示傅里叶变换。

卷积定理声称：

$ℱ\{g*h\}(s)=G(s)H(s),s\in ℝ$

$ℱ\{g\cdot h\}(s)=G(s)*H(s),s\in ℝ$

应用逆傅里叶变换${ℱ}^{-1}$产生推论：

$(g*h)(s)={ℱ}^{-1}\{G\cdot H\},s\in ℝ$

$(g\cdot h)(s)={ℱ}^{-1}\{G*H\},s\in ℝ$

这里的算符$\cdot$指示逐点乘法。

这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、梅林变换和Template:En-link等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。

周期卷积

对于周期为$P$的函数$g_{{}_P}(x)$和$h_{{}_P}(x)$，可以被表达为二者的Template:En-link：

$\begin{array}{cc}{g}_{{}_P}(x)& \triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}g(x-mP),m\in \mathbb{Z}\\ h_{{}_P}(x)& \triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}h(x-mP),m\in \mathbb{Z}\end{array}$

它们的傅里叶级数系数为：

$\begin{array}{cc}G[k]& \triangleq ℱ\{g_{{}_P}\}[k]=\frac{1}{P}\underset{P}{\int }{g}_{{}_P}(x)e^{-i2\pi kx/P}dx,k\in \mathbb{Z}\\ H[k]& \triangleq ℱ\{h_{{}_P}\}[k]=\frac{1}{P}\underset{P}{\int }{h}_{{}_P}(x)e^{-i2\pi kx/P}dx,k\in \mathbb{Z}\end{array}$

这里的$ℱ$算子指示傅里叶级数积分。

逐点乘积$g_{{}_P}(x)\cdot h_{{}_P}(x)$的周期也是$P$，它的傅里叶级数系数为：

$ℱ\{g_{{}_P}\cdot h_{{}_P}\}[k]=(G*H)[k]$

周期卷积$(g_{{}_P}*h)(x)$的周期也是$P$，周期卷积的卷积定理为：

$ℱ\{g_{{}_P}*h\}[k]=P\cdot G[k]H[k]$

离散卷积

对于作为两个连续函数采样的序列$g[n]$和$h[n]$，它们具有离散时间傅里叶变换$G(s)$和$H(s)$：

$\begin{array}{cc}G(s)& \triangleq ℱ\{g\}(s)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}g[n]\cdot e^{-i2\pi sn},s\in ℝ\\ H(s)& \triangleq ℱ\{h\}(s)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}h[n]\cdot e^{-i2\pi sn},s\in ℝ\end{array}$

这里的$ℱ$算子指示离散时间傅里叶变换（DTFT）。

离散卷积的卷积定理为：

$ℱ\{g*h\}(s)=G(s)H(s)$

离散周期卷积

对于周期为$N$的序列$g_{{}_N}[n]$和$h_{{}_N}[n]$：

$\begin{array}{cc}{g}_{{}_N}[n]& \triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}g[n-mN],m,n\in \mathbb{Z}\\ h_{{}_N}[n]& \triangleq \sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}h[n-mN],m,n\in \mathbb{Z}\end{array}$

相较于离散时间傅里叶变换$G(s)$和$H(s)$的周期是$1$，它们是按间隔$1/N$采样$G(s)$和$H(s)$，并在$N$个采样上进行了逆离散傅里叶变换（DFT^-1或IDFT）的结果。

离散周期卷积$(g_{{}_N}*h)[n]$的周期也是$N$。离散周期卷积定理为：

$ℱ\{g_{{}_N}*h\}[k]=\underset{G(k/N)}{\underbrace{ℱ\{g_{{}_N}\}[k]}}\cdot \underset{H(k/N)}{\underbrace{ℱ\{h_{{}_N}\}[k]}},k,n\in \mathbb{Z}$

这里的$ℱ$算子指示长度$N$的离散傅里叶变换（DFT）。

它有着推论：

$(g_{{}_N}*h)[n]={ℱ}^{-1}\{ℱ\{g_{{}_N}\}\cdot ℱ\{h_{{}_N}\}\}$

对于其非零时段小于等于$N$的$g$和$h$，离散圆周卷积的卷积定理为：

$(g_{{}_N}*h)[n]={ℱ}^{-1}\{ℱ\{g\}\cdot ℱ\{h\}\}$

推广

卷积的概念还可以推广到数列、测度以及广义函数上去。函数$f,g$是定義在${ℝ}^n$上的可測函數（measurable function），$f$与$g$存在卷积并记作$f*g$。如果函數不是定義在${ℝ}^n$上，可以把函數定義域以外的值都規定成零，這樣就變成一個定義在${ℝ}^n$上的函數。

若G是有某m 测度的群（例如豪斯多夫空间上哈尔测度下局部紧致的拓扑群），对于G上m-勒贝格可积的实数或复数函数f和g，可定义它们的卷积：

$(f*g)(x)=\underset{G}{\int }f(y)g(x{y}^{-1})dm(y)$

对于这些群上定义的卷积同样可以给出诸如卷积定理等性质，但是这需要对这些群的表示理论以及调和分析的彼得-外尔定理。

离散卷積的計算方法

計算卷積$f[n]*g[n]$有三種主要的方法，分別為

1. 直接計算（Direct Method）
2. 快速傅立葉轉換（FFT）
3. 分段卷積（sectioned convolution）

方法1是直接利用定義來計算卷積，而方法2和3都是用到了FFT來快速計算卷積。也有不需要用到FFT的作法，如使用數論轉換。

方法1：直接計算

• 作法：利用卷積的定義

$y[n]=f[n]*g[n]=\sum _{m=0}^{M-1}f[n-m]g[m]$

• 若$f[n]$和$g[n]$皆為實數信號，則需要$MN$個乘法。

• 若$f[n]$和$g[n]$皆為更一般性的複數信號，不使用複數乘法的快速演算法，會需要$4MN$個乘法；但若使用複數乘法的快速演算法，則可簡化至$3MN$個乘法。

因此，使用定義直接計算卷積的複雜度為$O(MN)$。

方法2：快速傅立葉轉換

• 概念：由於兩個離散信號在時域（time domain）做卷積相當於這兩個信號的離散傅立葉轉換在頻域（frequency domain）做相乘：

$y[n]=f[n]*g[n]\leftrightarrow Y[f]=F[f]G[f]$

，可以看出在頻域的計算較簡單。

• 作法：因此這個方法即是先將信號從時域轉成頻域：

$F[f]=DF{T}_P(f[n]),G[f]=DF{T}_P(g[n])$

，於是

$Y[f]=DF{T}_P(f[n])DF{T}_P(g[n])$

，最後再將頻域信號轉回時域，就完成了卷積的計算：

$y[n]=IDF{T}_{P}DF{T}_P(f[n])DF{T}_P(g[n])$

總共做了2次DFT和1次IDFT。

• 特別注意DFT和IDFT的點數$P$要滿足$P\ge M+N-1$。

• 由於DFT有快速演算法FFT，所以運算量為$O(P{\log }_{2}P)$

• 假設$P$點DFT的乘法量為$a$，$f[n]$和$g[n]$為一般性的複數信號，並使用複數乘法的快速演算法，則共需要$3a+3P$個乘法。

方法3：分段卷積

• 概念：將$f[n]$切成好幾段（section），每一段分別和$g[n]$做卷積後，再將結果相加。

• 作法：先將$f[n]$切成每段長度為$L$的區段（$L>M$），假設共切成S段：

$f[n](n=0,1,...,N-1)\to f_1[n],f_2[n],f_3[n],...,f_S[n](S=\lceil \frac{N}{L}\rceil )$

Section 1: $f_1[n]=f[n],n=0,1,...,L-1$

Section 2: $f_2[n]=f[n+L],n=0,1,...,L-1$

$⋮$

Section r: $f_r[n]=f[n+(r-1)L],n=0,1,...,L-1$

$⋮$

Section S: $f_S[n]=f[n+(S-1)L],n=0,1,...,L-1$

，$f[n]$為各個section的和

$f[n]=\sum _{r=1}^S{f}_r[n+(r-1)L]$。

因此，

$y[n]=f[n]*g[n]=\sum _{r=1}^S\sum _{m=0}^{M-1}{f}_r[n+(r-1)L-m]g[m]$，

每一小段作卷積則是採用方法2，先將時域信號轉到頻域相乘，再轉回時域：

$y[n]=IDFT(\sum _{r=1}^S\sum _{m=0}^{M-1}DF{T}_P(f_r[n+(r-1)L-m])DF{T}_P(g[m])),P\ge M+L-1$。

• 總共只需要做$P$點FFT $2S+1$次，因為$g[n]$只需要做一次FFT。

• 假設$P$點DFT的乘法量為$a$，$f[n]$和$g[n]$為一般性的複數信號，並使用複數乘法的快速演算法，則共需要$(2S+1)a+3SP$個乘法。

• 運算量：$\frac{N}{L}3(L+M-1)[{\log }_2(L+M-1)+1]$

• 運算複雜度：$O(N)$，和$N$呈線性，較方法2小。
• 分為 Overlap-Add 和 Overlap-Save 兩種方法。

分段卷積: Overlap-Add

欲做$x[n]*h[n]$的分段卷積分，$x[n]$ 長度為 $N$，$h[n]$ 長度為 $M$,

Step 1: 將$x[n]$每 $L$ 分成一段

Step 2: 再每段 $L$ 點後面添加 $M-1$ 個零，變成長度 $L+M-1$

Step 3: 把 $h[n]$ 添加 $L-1$個零，變成長度 $L+M-1$的 $h^{\prime }[n]$

Step 4: 把每個 $x[n]$ 的小段和 $h^{\prime }[n]$ 做快速卷積，也就是$IDF{T}_{L+M-1}\{DF{T}_{L+M-1}(x[n])DF{T}_{L+M-1}(h^{\prime }[n])\}$，每小段會得到長度 $L+M-1$ 的時域訊號

Step 5: 放置第 $i$ 個小段的起點在位置 $L\times i$ 上, $i=0,1,...,\lceil \frac{N}{L}\rceil -1$

Step 6: 會發現在每一段的後面 $M-1$ 點有重疊，將所有點都相加起來，顧名思義 Overlap-Add，最後得到結果

舉例來說:

$x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]$, 長度 $N=15$

$h[n]=[1,2,3]$, 長度 $M=3$

令

$L=5$

• 
  x[n]和h[n]

令

$L=5$

切成三段，分別為

$x_0[n],x_1[n],x_2[n]$

, 每段填

$M-1$

個零，並將

$h[n]$

填零至長度

$L+M-1$

• 
  分段x[n]

將每一段做

$IDF{T}_{L+M-1}\{DF{T}_{L+M-1}(x[n])DF{T}_{L+M-1}(h^{\prime }[n])\}$

• 
  分段運算結果

若將每小段擺在一起，可以注意到第一段的範圍是

$0\sim 6$

，第二段的範圍是

$5\sim 11$

，第三段的範圍是

$10\sim 16$

，三段的範圍是有重疊的

• 
  合併分段運算結果

最後將三小段加在一起，並將結果和未分段的卷積做比較，上圖是分段的結果，下圖是沒有分段並利用快速卷積所算出的結果，驗證兩者運算結果相同。

• 
  結果比較圖

分段卷積: Overlap-Save

欲做$x[n]*h[n]$的分段卷積分，$x[n]$ 長度為 $N$，$h[n]$ 長度為 $M$,

Step 1: 將 $x[n]$ 前面填 $M-1$ 個零

Step 2: 第一段 $i=0$, 從新的 $x[n]$ 中 $L\times i-(M-1)\times i$ 取到 $L\times (i+1)-(M-1)\times i-1$ 總共 $L$ 點當做一段，因此每小段會重複取到前一小段的 $M-1$ 點，取到新的一段全為零為止

Step 3: 把 $h[n]$ 添加 $L-M$ 個零，變成長度 $L$ 的 $h^{\prime }[n]$

Step 4: 把每個 $x[n]$ 的小段和 $h^{\prime }[n]$ 做快速卷積，也就是$IDF{T}_L\{DF{T}_L(x[n])DF{T}_L(h^{\prime }[n])\}$，每小段會得到長度 $L$ 的時域訊號

Step 5: 對於每個 $i$ 小段，只會保留末端的 $L-(M-1)$ 點，因此得名 Overlap-Save

Step 6: 將所有保留的點合再一起，得到最後結果

舉例來說:

$x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]$, 長度 $N=15$

$h[n]=[1,2,3]$, 長度 $M=3$

令

$L=7$

• 
  x[n]和h[n]

將

$x[n]$

前面填

$M-1$

個零以後，按照 Step 2 的方式分段，可以看到每一段都重複上一段的

$M-1$

點

• 
  分段x[n]

再將每一段做

$IDF{T}_L\{DF{T}_L(x[n])DF{T}_L(h^{\prime }[n])\}$

以後可以得到

• 
  分段運算結果

保留每一段末端的

$L-(M-1)$

點，擺在一起以後，可以注意到第一段的範圍是

$0\sim 4$

，第二段的範圍是

$5\sim 9$

，第三段的範圍是

$10\sim 14$

，第四段的範圍是

$15\sim 16$

，四段的範圍是沒有重疊的

• 
  合併分段運算結果

將結果和未分段的卷積做比較，下圖是分段的結果，上圖是沒有分段並利用快速卷積所算出的結果，驗證兩者運算結果相同。

• 
  結果比較圖

至於為什麼要把前面

$M-1$

丟掉?

以下以一例子來闡述:

$x[n]=[1,2,3,4,5,6,7,8,9,10]$, 長度 $L=10$，

$h[n]=[1,2,3,4,5]$, 長度 $M=5$,

第一條藍線代表

$y$

軸，而兩條藍線之間代表長度

$L$

，是在做快速摺積時的週期

• 
  x[n]和h[n]

當在做快速摺積時

$IDF{T}_L\{DF{T}_L(x[n])DF{T}_L(h^{\prime }[n])\}$

，是把訊號視為週期

$L$

，在時域上為循環摺積分,

而在一開始前 $M-1$ 點所得到的值，是 $h[0],h[6],h[7],h[8],h[9]$ 和 $x[0],x[6],x[7],x[8],x[9]$ 內積的值，

然而 $h[6],h[7],h[8],h[9]$ 這 $M-1$ 個值應該要為零，以往在做快速摺積時長度為 $L+M-1$ 時不會遇到這些問題，

而今天因為在做快速摺積時長度為

$L$

才會把這

$M-1$

點算進來，因此我們要丟棄這

$M-1$

點內積的結果

• 
  循環摺積

為了要丟棄這

$M-1$

點內積的結果，位移

$h[-n]$ $M-1$

點，並把位移以後內積合的值才算有效。

• 
  位移以後內積

應用時機

以上三種方法皆可用來計算卷積，其差別在於所需總體乘法量不同。基於運算量以及效率的考量，在計算卷積時，通常會選擇所需總體乘法量較少的方法。

以下根據$f[n]$和$g[n]$的長度（$N,M$）分成5類，並列出適合使用的方法：

1. $M$為一非常小的整數 - 直接計算
2. $M\ll N$ - 分段卷积
3. $M\approx N$ - 快速傅里叶变换
4. $M\gg N$ - 分段卷积
5. $N$為一非常小的整數 - 直接計算

基本上，以上只是粗略的分類。在實際應用時，最好還是算出三種方法所需的總乘法量，再選擇其中最有效率的方法來計算卷積。

例子

Q1：當$N=2000,M=17$，適合用哪種方法計算卷積?

Ans：

方法1：所需乘法量為$3MN=102000$

方法2：$P\ge M+N-1=2016$，而2016點的DFT最少乘法數$a=12728$，所以總乘法量為$3(a+P)=44232$

方法3：

若切成8塊（$S=8$），則$L=250,P\ge M+L-1=266$。選$P=288$，則總乘法量為$(2S+1)a+3SP=26632$，比方法1和2少了很多。

但是若要找到最少的乘法量，必須依照以下步驟

(1)先找出$L$:解$L$ : $\frac{\partial \frac{N}{L}3(L+M-1)[{\log }_2(L+M-1)+1]}{\partial L}=0$

(2)由$P\ge L+M-1$算出點數在$P$附近的DFT所需最少的乘法量，選擇DFT的點數

(3)最後由$L=P+1-M$算出$L_{opt}$

因此，

(1)由運算量對$L$的偏微分為0而求出$L=85$

(2)$P\ge L+M-1=101$，所以選擇101點DFT附近點數乘法量最少的點數$P=96$或$P=120$。

(3-1)當$P=96\to a=280,L=P+1-M=80\to S=25$，總乘法量為$(2S+1)a+3SP=21480$。

(3-2)當$P=120\to a=380,L=P+1-M=104\to S=20$，總乘法量為$(2S+1)a+3SP=22780$。

由此可知，切成20塊會有較好的效率，而所需總乘法量為21480。

• 因此，當$N=2000,M=17$，所需總乘法量：分段卷積<快速傅立葉轉換<直接計算。故，此時選擇使用分段卷積來計算卷積最適合。

Q2：當$N=1024,M=3$，適合用哪種方法計算卷積?

Ans：

方法1：所需乘法量為$3MN=9216$

方法2：$P\ge M+N-1=1026$，選擇1026點DFT附近點數乘法量最少的點數，$\to P=1152,a=7088$。

因此，所需乘法量為$3(a+P)=24342$

方法3：

(1)由運算量對$L$的偏微分為0而求出$L=5$

(2)$P\ge L+M-1=7$，所以選擇7點DFT附近點數乘法量最少的點數$P=8$或$P=6$或$P=4$。

(3-1)當$P=8\to a=4,L=P+1-M=6\to S=171$，總乘法量為$(2S+1)a+3SP=5476$。

(3-2)當$P=6\to a=4,L=P+1-M=4\to S=256$，總乘法量為$(2S+1)a+3SP=6660$。

(3-3)當$P=4\to a=0,L=P+1-M=2\to S=512$，總乘法量為$(2S+1)a+3SP=6144$。

由此可知，切成171塊會有較好的效率，而所需總乘法量為5476。

• 因此，當$N=1024,M=3$，所需總乘法量：分段卷積<直接計算<快速傅立葉轉換。故，此時選擇使用分段卷積來計算卷積最適合。
• 雖然當$M$是個很小的正整數時，大致上適合使用直接計算。但實際上還是將3個方法所需的乘法量都算出來，才能知道用哪種方法可以達到最高的效率。

Q3：當$N=1024,M=600$，適合用哪種方法計算卷積?

Ans：

方法1：所需乘法量為$3MN=1843200$

方法2：$P\ge M+N-1=1623$，選擇1026點DFT附近點數乘法量最少的點數，$\to P=2016,a=12728$。

因此，所需乘法量為$3(a+P)=44232$

方法3：

(1)由運算量對$L$的偏微分為0而求出$L=1024$

(2)$P\ge L+M-1=1623$，所以選擇1623點DFT附近點數乘法量最少的點數$P=2016$。

(3)當$P=2016\to a=12728,L=P+1-M=1417\to S=1$，總乘法量為$(2S+1)a+3SP=44232$。

由此可知，此時切成一段，就跟方法2一樣，所需總乘法量為44232。

• 因此，當$N=1024,M=600$，所需總乘法量：快速傅立葉轉換 = 分段卷積<直接計算。故，此時選擇使用分段卷積來計算卷積最適合。

应用

高斯模糊可被用来从半色调印刷品复原出光滑灰度数字图像。

卷积在科学、工程和数学上都有很多应用：

• 代数中，整数乘法和多项式乘法都是卷积。
• 卷积神经网络应用了多重级联的卷积Template:En-link，它被用于机器视觉和人工智能，尽管在多数情况下实际上用的是互相关而非卷积。
• 在非人工智能的图像处理中，用作图像模糊、锐化、边缘检测。
• 统计学中，加权的滑动平均是一种卷积。
• 概率论中，两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
• 声学中，回声可以用源声与一个反映各种反射效应的函数的卷积表示。
• 电子工程与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。
• 物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

参见

• 反卷积
• 自相关函数
• 傅里叶变换

延伸阅读

• Template:Citation.
• Template:Citation
• Template:Citation
• Dominguez-Torres, Alejandro (Nov 2, 2010). "Origin and history of convolution". 41 pgs. -{R|http://www.slideshare.net/Alexdfar/origin-adn-history-of-convolution}- Template:Wayback. Cranfield, Bedford MK43 OAL, UK. Retrieved Mar 13, 2013.
• Template:Citation
• Template:Citation
• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Narici Beckenstein Topological Vector Spaces
• Template:Citation
• Template:Citation.
• Template:Schaefer Wolff Topological Vector Spaces
• Template:Citation.
• Template:Springer.
• Template:Citation.
• Template:Citation.
• Template:Trèves François Topological vector spaces, distributions and kernels
• Template:Citation
• Template:Citation.
• Template:Cite book
• Template:Cite book

外部链接

• Earliest Uses: The entry on Convolution has some historical information. Template:Wayback
• Convolution, on The Data Analysis BriefBook
• -{R|http://www.jhu.edu/~signals/convolve/index.html}- Template:Wayback Visual convolution Java Applet
• -{R|http://www.jhu.edu/~signals/discreteconv2/index.html}- Template:Wayback Visual convolution Java Applet for discrete-time functions
• -{R|https://get-the-solution.net/projects/discret-convolution}- discret-convolution online calculator
• -{R|https://lpsa.swarthmore.edu/Convolution/CI.html}- Template:Wayback Convolution demo and visualization in javascript
• -{R|https://phiresky.github.io/convolution-demo/}- Template:Wayback Another convolution demo in javascript
• Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters
• * -{R|https://archive.org/details/Lectures_on_Image_Processing}-
• Convolution Kernel Mask Operation Interactive tutorial Template:Wayback
• Convolution Template:Wayback at MathWorld
• Freeverb3 Impulse Response Processor Template:Wayback: Opensource zero latency impulse response processor with VST plugins
• Stanford University CS 178 interactive Flash demo Template:Wayback showing how spatial convolution works.
• A video lecture on the subject of convolution Template:Wayback given by Salman Khan
• Example of FFT convolution for pattern-recognition (image processing) Template:Wayback
• Intuitive Guide to Convolution Template:Wayback A blogpost about an intuitive interpretation of convolution.