叶状结构

里布叶状结构的2维截面

里布叶状结构的3维模型

微分几何中，叶状结构（Template:Lang）是n-流形上的等价关系，等价类是连通单射浸入子流形，都具有相同维度p，以实坐标空间${ℝ}^n$的分解为标准嵌入子空间${ℝ}^p$的陪集$x+{ℝ}^p$为模型。等价类称作叶状结构的叶（leaf）。若要求流形和/或子流形具有（$C^r$类的）分段线性、微分或解析结构，就可分别定义分段线性、微分、解析叶状结构。在最重要的$C^r$类微分叶状结构中，通常r ≥ 1（否则$C^0$就是拓扑叶状结构）。p（叶的维度）称作叶状结构的维度，$q=n-p$称作其余维数。

在数学物理学家关于广义相对论的一些论文中，“叶状结构”用于描述：相关的洛伦兹流形（(p+1)维时空）分解为p维超平面，指定为梯度处处不为零的实值光滑函数（标量场）的水平集；这光滑函数通常被假定为时间函数，梯度处处类时间，因此其水平集都是类空间超平面。为与标准数学术语保持一致，这些超平面通常称作叶状结构的叶。注意，虽然这情形确实构成标准数学意义上的余维-1叶状结构，但这类例子是全局平凡的。虽然（数学）余维-1叶状结构的叶局部上总是函数的水平集，但一般不能在全局这样表达，因为叶可能无限多次通过局部平凡化坐标图，叶周围的完整也可能阻碍叶的全局一致定义函数的存在。例如，虽然3-球面有一个由里布发现的余维1-叶状结构，但闭流形的余维-1叶状结构不能由光滑函数的水平集给出，因为闭流形上的光滑函数必然在最值点有临界点。

叶状结构好比是一种给流形穿的条纹织物的衣服。在流形的每个足够小的片上，这些条纹给了流形一个局部乘积结构，不需在局部区域之外一致（不用有良定义的整体结构）：沿着一个条纹走足够远，可能回到不同的邻近的条纹。

叶状图与图册

为给叶状结构下精确定义，需先定义一些辅助元素。

3维叶状图（foliated chart），n = 3、q = 1。斑（plaque）是2维的，横截（transversal）是1维的。

${ℝ}^n$中的矩邻域是形式为$B=J_1\times \cdots \times J_n$的开子集，其中$J_i$是第i个坐标轴上（可能无界）的相对开区间。若$J_1$具有形式$(a,0]$，则称B具有边界

$\partial B=\{(0,x^2,\dots ,x^n)\in B\}.$

在下面的定义中，坐标图（coordinate chart）被认为是在${ℝ}^p\times {ℝ}^q$，允许流形具有边界和（凸）角的可能。

n-流形M上余维为q的叶状图（foliated chart）是$(U,\phi )$，其中$U\subset M$是开集，$\phi :U\to B_{\tau }\times B_{⋔}$是微分同胚，$B_{⋔}$是${ℝ}^q$中的矩邻域，$B_{\tau }$是${ℝ}^p$中的矩邻域。集合$P_y={\phi }^{-1}(B_{\tau }\times \{y\})$，其中$y\in B_{⋔}$称作这叶状图的斑（plaque）。$\mathrm{\forall }x\in B_{\tau }$，集合$S_x={\phi }_x={\phi }^{-1}(\{x\}\times B_{⋔})$称作叶状图的横截（transversal）。集合${\partial }_{\tau }U={\phi }^{-1}(B_{\tau }\times (\partial B_{⋔}))$称作U的切边界（tangential boundary），${\partial }_{⋔}U={\phi }^{-1}((\partial B_{\tau })\times B_{⋔})$称作U的横截边界（transverse boundary）。

叶状图是所有叶状结构的基本模型，斑就是叶。$B_{\tau }$表示“B-切”，$B_{⋔}$表示“B-截”。还有多种可能。若$B_{⋔},B_{\tau }$都有空边界，则叶状图就建模了无界n-流形的余维-q叶状结构。若其中一个矩邻域有界，则叶状图建模了有界无角n-流形的叶状结构的各种可能性。具体来说，若$\partial B_{⋔}\ne \varnothing =\partial B_{\tau }$，则$\partial U={\partial }_{\tau }U$是斑之并，斑表示的叶状结构切于边界。若$\partial B_{\tau }\ne \varnothing =\partial B_{⋔}$，则$\partial U={\partial }_{⋔}U$是横截之并，叶状结构横截于边界。最后，若$\partial B_{⋔}\ne \varnothing \ne \partial B_{\tau }$，则建模了叶状流形（foliated manifold），角分开了切边界与横截边界。

(a) 与边界相切的叶状结构$\partial B_{⋔}\ne \varnothing =\partial B_{\tau }$； (b) 与边界相截的叶状结构$\partial B_{\tau }\ne \varnothing =\partial B_{⋔}$； (c) 角将切边界与横截边界隔开的叶状结构$\partial B_{⋔}\ne \varnothing \ne \partial B_{\tau }$。

n-流形M上余维为q的$C^r(0\le r\le \mathrm{\infty })$类叶状图册（foliated atlas）是余维为q的叶状图的$C^r$-图册$𝒰=\{(U_{\alpha },{\phi }_{\alpha })\mid \alpha \in A\}$，只要P、Q在$𝒰$的不同图中都是斑，P ∩ Q在P、Q中都是开的，它们就是相干叶状结构（coherently foliated）。

重新表述相干叶状图的有效方法是将$w\in U_{\alpha }\cap U_{\beta }$写作：

${\phi }_{\alpha }(w)=(x_{\alpha }(w),y_{\alpha }(w))\in B_{\tau }^{\alpha }\times B_{⋔}^{\alpha },$

${\phi }_{\beta }(w)=(x_{\beta }(w),y_{\beta }(w))\in B_{\tau }^{\beta }\times B_{⋔}^{\beta }.$

$(U_{\alpha },{\phi }_{\alpha })$常写作$(U_{\alpha },x_{\alpha },y_{\alpha })$，其中

$x_{\alpha }=(x_{\alpha }^1,\dots ,x_{\alpha }^p),$

$y_{\alpha }=(y_{\alpha }^1,\dots ,y_{\alpha }^q).$

在${\phi }_{\beta }(U_{\alpha }\cap U_{\beta })$上，坐标公式可改写为

$g_{\alpha \beta }(x_{\beta },y_{\beta })={\phi }_{\alpha }\circ {\phi }_{\beta }^{-1}(x_{\beta },y_{\beta })=(x_{\alpha }(x_{\beta },y_{\beta }),y_{\alpha }(x_{\beta },y_{\beta })).$

$U_{\alpha }$的每个斑都会遇到$U_{\beta }$的2个斑。

$(U_{\alpha },x_{\alpha },y_{\alpha }),(U_{\beta },x_{\beta },y_{\beta })$是相干叶状结构这一条件意味着，若$P\subset U_{\alpha }$是斑，则$P\cap U_{\beta }$的连通分量位于$U_{\beta }$的（可能不同的）斑中。等价地，由于$U_{\alpha },U_{\beta }$的斑分别是横坐标$y_{\alpha },y_{\beta }$的水平集，$\mathrm{\forall }z\in U_{\alpha }\cap U_{\beta }$都有邻域，其中公式

$y_{\alpha }=y_{\alpha }(x_{\beta },y_{\beta })=y_{\alpha }(y_{\beta })$

与$x_{\beta }$无关。

叶状图册的主要用处是将重叠的斑连接起来，形成叶状结构；上述一般定义显得有点笨拙，一个问题是，$(U_{\alpha },{\phi }_{\alpha })$的斑可以与多个$(U_{\beta },{\phi }_{\beta })$的斑相遇。甚至可能出现，一个图的斑与另一图的无穷多个斑相遇。不过，如下所示，假设情形更规则，也不失一般性。

若$𝒰\cup 𝒱$是叶状$C^r$图册，则M上两具有相同余维和光滑度的$C^r$类叶状图册$𝒰,𝒱$是相干的：$(𝒰\approx 𝒱)$。叶状图册的相干是等价关系。

证明

自反关系和对称关系是直接的。要证传递关系，令$𝒰\approx 𝒱$ and $𝒱\approx 𝒲$。令$(U_{\alpha },x_{\alpha },y_{\alpha })\in 𝒰,(W_{\lambda },x_{\lambda },y_{\lambda })\in 𝒲$，并假设有点$w\in U_{\alpha }\cap W_{\lambda }$。择$(V_{\delta },x_{\delta },y_{\delta })\in 𝒱$，使得$w\in V_{\delta }$。根据上述说明，w有属于$U_{\alpha }\cap V_{\delta }\cap W_{\lambda }$的邻域，使得 $y_{\delta }=y_{\delta }(y_{\lambda })\text{on}{\phi }_{\lambda }(N),$ $y_{\alpha }=y_{\alpha }(y_{\delta })\text{on}{\phi }_{\delta }(N),$ 由此 $y_{\alpha }=y_{\alpha }(y_{\delta }(y_{\lambda }))\text{on}{\phi }_{\delta }(N).$ 由于$w\in U_{\alpha }\cap W_{\lambda }$是任意的，可以总结$y_{\alpha }(x_{\lambda },y_{\lambda })$局部依赖于$x_{\lambda }$。于是可以证明$𝒰\approx 𝒲$，因为相干是可传递的。

规则叶状图册中的图。

上面定义的开集上的斑与横截也是开的。不过，我们也可以谈论闭的斑与横截：若$(U,\phi ),(W,\psi )$都是叶状图，使得$\bar{U}$（U的闭包）是W的子集，$\phi =\psi |U$；则，若$\phi (U)=B_{\tau }\times B_{⋔},$可知$\psi |\bar{U}$，写作$\bar{\phi }$，将$\bar{U}$微分同胚地带到${\bar{B}}_{\tau }\times {\bar{B}}_{⋔}.$

符合以下条件的叶状图册称作规则的（regular）：

1. $\mathrm{\forall }\alpha \in A,{\bar{U}}_{\alpha }$是叶状图$(W_{\alpha },{\psi }_{\alpha })$的紧子集，且${\phi }_{\alpha }={\psi }_{\alpha }|U_{\alpha }$；
2. 覆盖$\{U_{\alpha }|\alpha \in A\}$是局部有限的；
3. 若$(U_{\alpha },{\phi }_{\alpha }),(U_{\beta },{\phi }_{\beta })$都是叶状图册的元素，则每个闭斑$P\subset {\bar{U}}_{\alpha }$的内部与最多与${\bar{U}}_{\beta }$中的1个斑相遇。

根据性质 (1)，坐标$x_{\alpha },y_{\alpha }$延伸到${\bar{U}}_{\alpha }$上的坐标${\bar{x}}_{\alpha },{\bar{y}}_{\alpha }$，可以写成${\bar{\phi }}_{\alpha }=({\bar{x}}_{\alpha },{\bar{y}}_{\alpha }).$性质 (3)等价于要求：若$U_{\alpha }\cap U_{\beta }\ne \varnothing$，横坐标变化${\bar{y}}_{\alpha }={\bar{y}}_{\alpha }({\bar{x}}_{\beta },{\bar{y}}_{\beta })$独立于${\bar{x}}_{\beta }.$即

${\bar{g}}_{\alpha \beta }={\bar{\phi }}_{\alpha }\circ {\bar{\phi }}_{\beta }^{-1}:{\bar{\phi }}_{\beta }({\bar{U}}_{\alpha }\cap {\bar{U}}_{\beta })\to {\bar{\phi }}_{\alpha }({\bar{U}}_{\alpha }\cap {\bar{U}}_{\beta })$

有公式

${\bar{g}}_{\alpha \beta }({\bar{x}}_{\beta },{\bar{y}}_{\beta })=({\bar{x}}_{\alpha }({\bar{x}}_{\beta },{\bar{y}}_{\beta }),{\bar{y}}_{\alpha }\left({\bar{y}}_{\beta }\right)).$

类似论断也适于开图（无覆盖线）。横坐标映射$y_{\alpha }$可视作浸没

$y_{\alpha }:U_{\alpha }\to {ℝ}^q$

公式$y_{\alpha }=y_{\alpha }(y_{\beta })$可视作微分同胚

${\gamma }_{\alpha \beta }:y_{\beta }(U_{\alpha }\cap U_{\beta })\to y_{\alpha }(U_{\alpha }\cap U_{\beta }).$

它们满足上循环条件，即，在$y_{\delta }(U_{\alpha }\cap U_{\beta }\cap U_{\delta })$上，

${\gamma }_{\alpha \delta }={\gamma }_{\alpha \beta }\circ {\gamma }_{\beta \delta }$

尤其是，

${\gamma }_{\alpha \alpha }\equiv y_{\alpha }\left(U_{\alpha }\right),$

${\gamma }_{\alpha \beta }={\gamma }_{\beta \alpha }^{-1}.$

用上述关于相干性和规则性的定义，可证明每个叶状图册都有规则的相干细化。

证明

固定M上的一个度量核一个叶状图册$𝒲.$传递到子覆盖，如有必要，可假设$𝒲={\{W_j,{\psi }_j\}}_{j=1}^l$有限。令ε > 0是$𝒲$的勒贝格数，即直径< ε的$\mathrm{\forall }\subset X\subseteq M$都完全位于某个$W_j$中。$\mathrm{\forall }x\in M$，择j使得$x\in W_j$、择叶状图$(U_x,{\phi }_x)$使得 $x\in U_x\subseteq {\bar{U}}_x\subset W_j,$ ${\phi }_x={\psi }_j|U_x,$ $\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}(U_x)<\epsilon /2.$ 设$U_x\subset W_k(k\ne j)$，并照常记${\psi }_k=(x_k,y_k)(y_k:W_k\to {ℝ}^q)$是横坐标映射。这是浸没，以$W_k$中的斑为水平集。因此，$y_k$限制到浸没$y_k:U_x\to {ℝ}^q.$ 这在$x_j$中是局部为常的；因此，若有必要可以选择较小的$U_x$，假定$y_k|{\bar{U}}_x$以${\bar{U}}_x$的斑为水平集。即，$W_k$的斑最多与${\bar{U}}_x$的一个（紧）斑相遇（因此包含）。由于1 < k < l < ∞，可以择$U_x$，使得只要$U_x\subset W_k$，${\bar{U}}_x$的不同斑就位于$W_k$的不同斑中。传递到$\{(U_x,{\phi }_x)|x\in M\}$的有限子图册$𝒰={\{U_i,{\phi }_i\}}_{i=1}^N$。若$U_i\cap U_j\ne 0,\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}(U_i\cup U_j)<\epsilon$，于是存在索引k使得${\bar{U}}_i\cup {\bar{U}}_j\subseteq W_k$。${\bar{U}}_i$的不同斑（分别是${\bar{U}}_j$的不同斑）位于$W_k$的不同斑中。因此${\bar{U}}_i$的每个斑内部最多与${\bar{U}}_j$的一个斑相交，反之亦然。根据构造，$𝒰$是$𝒲$的相干细化，是规则叶状图册。 若M非紧，局部紧性和第二可数性允许我们选择紧子集序列${\left\{K_i\right\}}_{i=0}^{\mathrm{\infty }}$，使得$\mathrm{\forall }i\ge 0,M=\bigcup _{i=1}^{\mathrm{\infty }}{K}_i,K_i\subset \mathrm{i}\mathrm{n}\mathrm{t}{K}_{i+1}$。传递到子图集，假定$𝒲={\{W_j,{\psi }_j\}}_{j=0}^{\mathrm{\infty }}$可数，且可找到严格递增正整数列${\left\{n_l\right\}}_{l=0}^{\mathrm{\infty }}$使${𝒲}_l={\{W_j,{\psi }_j\}}_{j=0}^{n_l}$是$K_l$的覆盖。令${\delta }_l$表示$K_l$到$\partial K_{l+1}$的距离，并择${\epsilon }_l>0$，小到对于$l\ge 1,{\epsilon }_0<{\delta }_0/2$，都有${\epsilon }_l<\mathrm{m}\mathrm{i}\mathrm{n}\{{\delta }_l/2,{\epsilon }_{l-1}\}$（${\epsilon }_l$是${𝒲}_l$（作为$K_l$的开覆盖）与${𝒲}_{l+1}$（作为$K_{l+1}$的开覆盖）的勒贝格数）。更确切地说，若$X\subset M$与$L_l$相遇（或$K_{l+1}$），且$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}X<{\epsilon }_l$，则X位于${𝒲}_l$的某个元素中（或${𝒲}_{l+1}$）。$\mathrm{\forall }x\in K_l╲\mathrm{i}\mathrm{n}\mathrm{t}{K}_{l-1}$，与紧情形一样构造$(U_x,{\phi }_x)$，要求${\bar{U}}_x$是$W_j$的紧子集，且$\mathrm{\forall }j\le n_l,{\phi }_x={\psi }_j|U_x$。同时，要求$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}{\bar{U}}_x<{\epsilon }_l/2$。和之前一样，传递到$K_l╲\mathrm{i}\mathrm{n}\mathrm{t}{K}_{l-1}$的有限子覆盖${\{U_i,{\phi }_i\}}_{i=n_{l-1}+1}^{n_l}$（此处取$n_{-1}=0$。）这样就创造了规则叶状图册$𝒰={\{U_i,{\phi }_i\}}_{i=1}^{\mathrm{\infty }}$，细化了$𝒲$并与$𝒲$相干。

叶状结构的定义

根据实现叶状结构的方式，有几种不同的定义。最常见方式是通过流形分解，得到

通过坐标函数$x:U\to {ℝ}^n$分解

定义 n维流形M的p-维$C^r$类叶状结构是将M分解为不交连通子流形$\{L_{\alpha }{\}}_{\alpha \in A}$的并，称作叶状结构的叶（leaf），具有如下性质：M的点都有邻域U和局部$C^r$类坐标系$x=(x^1,\dots ,x^n):U\to {ℝ}^n$，使得对每片叶$L_{\alpha }$，$U\cap L_{\alpha }$的组分都由方程组$x^{p+1}=\text{常数},\dots ,x^n=\text{常数}$描述。则，叶状结构记作$ℱ=\{L_{\alpha }{\}}_{\alpha \in A}.$

叶的概念可以让我们直观地思考叶状结构。若用稍微几何化的定义，n维流形M的p维叶状结构$ℱ$也许可简单视作M的逐对不交、连通浸没的p维子流形（叶状结构的叶）的集合$\{M_a\}$，使得对点$\mathrm{\forall }x\in M$，都有图$(U,\phi )$，其中U同胚于${ℝ}^n$，包含的x使得对每片叶$M_a$，与U相遇或为空集或为子空间的可数集，其在$\phi (M_a\cap U)$中$\phi$的像下是前n-p个坐标为常数的p维仿射子空间。

叶状结构局部上都是浸没，允许下列定义

定义 令M、Q是n维流形，q≤n，并令$f:M\to Q$是浸没，即假设函数微分矩阵（雅可比矩阵）的秩为q，则据隐函数定理，ƒ在M上诱导了余维为q的叶状结构，其中的叶定义为$x\in Q,f^{-1}(x).$

这定义描述了n维流形M的p维叶状结构$ℱ$，是由图（chart）$U_i$与下列映射覆盖的：

${\phi }_i:U_i\to {ℝ}^n$

这样，对重叠对$U_i,U_j$，转移函数${\phi }_{ij}:{ℝ}^n\to {ℝ}^n$定义为

${\phi }_{ij}={\phi }_j{\phi }_i^{-1}$

形式为

${\phi }_{ij}(x,y)=({\phi }_{ij}^1(x),{\phi }_{ij}^2(x,y))$

其中x表示前$q=n-p$个坐标，y表示后p个坐标（co-ordinates），即

$\begin{array}{cc}{\phi }_{ij}^1:& {ℝ}^q\to {ℝ}^q\\ {\phi }_{ij}^2:& {ℝ}^n\to {ℝ}^p\end{array}$

将转移函数${\phi }_{ij}$拆分为${\phi }_{ij}^1(x),{\phi }_{ij}^2(x,y)$，作为浸没的一部分完全类似于将${\bar{g}}_{\alpha \beta }$拆分为${\bar{y}}_{\alpha }\left({\bar{y}}_{\beta }\right),{\bar{x}}_{\alpha }({\bar{x}}_{\beta },{\bar{y}}_{\beta })$，作为规则叶状图册定义的一部分。这使得可以用规则叶状图册定义叶状结构成为可能。为此，必须首先证明，余维度为q的规则叶状图册都与唯一的余维度为q的叶状结构$ℱ$相关联。

证明

令$𝒰={\{U_a,{\phi }_{\alpha }\}}_{\alpha \in A}$是余维为q的规则叶状图册。在M上定义等价关系：x ~ y，当且仅当$\mathrm{\exists }𝒰$-斑$P_0$使得$x,y\in P_0$，或有$𝒰$-斑的序列$L=\{P_0,P_1,\dots ,P_p\}$使得$x\in P_0,y\in P_p,P_i\cap P_{i-1}\ne \varnothing (1\le i\le p)$成立。称序列L为连接x、y的长p的斑链。$x,y\in P_0$时，可以说$\{P_0\}$是连接x、y的长度为0的斑链。~是等价关系，这很清楚；同样明显的是，等价类L都是斑的并。由于$𝒰$-斑只能在彼此的开子集中相互重叠，所以L在局部是维度为n-q的拓扑浸入（immerse）子流形。斑$P\subset L$的开子集在L上构成了n-q维的局部欧氏拓扑的基，L在这拓扑中显然是连通的。要检验L是否为豪斯多夫空间也是平凡的，主要问题是要证明L第二可数。由于斑都是第二可数的，所以对L只需证L中$𝒰$-斑集最多为可数无穷。固定一个这样的斑$P_0$，根据规则叶状图册的定义，其只与有限多个其他斑相遇。即，只有有限多长1的斑链$\{P_0,P_i\}$。归纳始于$P_0$的p长斑链，同样可证明长度≤ p的斑链只有有限多条。根据~的定义，L中所有$𝒰$-斑都可通过始于$P_0$的有限斑链抵达，因此可得上述论断。

正如证明所示，叶状结构的叶是长度 ≤ p的斑链的等价类，也是拓扑浸入豪斯多夫p维子流形。接着，我们将证明叶上斑的等价关系可用相干叶状图册的等价来表示，即它们与叶状结构的联系。更具体地说，若$𝒰,𝒱$是M上的叶状图册、且若$𝒰$与叶状结构$ℱ$相关联，则当且仅当$𝒱$也与$ℱ$相关联时，$𝒰,𝒱$相干。

证明
若$𝒱$也与$ℱ$相关联，则每片叶L都是$𝒱$-斑与$𝒰$-斑的并。这些斑在L的流形拓扑中是开子集，因此交于彼此的开子集。由于斑是连通的，所以不在同一片叶的$𝒰$-斑不能交$𝒱$-斑；因此叶状图册是相干的。反之，若只知道$𝒰$与$ℱ$相关联、$𝒱\approx 𝒰$，令Q是$𝒱$-斑。若L是$ℱ$的叶，且$w\in L\cap Q(w\in P)$，令$P\in L$是$𝒰$-斑，则$P\cap Q$是w在Q中的开邻域，且$P\cap Q\subset L\cap Q$。由于$w\in L\cap Q$是任意的，可知$L\cap Q$是开的；由于L也是任意的叶，所以Q可分解为不交的开子集，每个都是Q与$ℱ$中某叶的交。又由于Q连通，$L\cap Q=Q.$最后，Q也是任意的$𝒱$-斑，所以$𝒱$与$ℱ$相关联。

现在很明显，M上的叶状结构与叶状图册间的关联关系产生了M的叶状结构集同叶状图册的相干类集之间的一一对应，换句话说，M上余维为q的$C^r$类叶状结构$ℱ$是余维为q的$C^r$类叶状图册的相干类。据佐恩引理，叶状图册相干类显然包含唯一的最大叶状图册。于是，

定义 M上余维为q的$C^r$类叶状结构是M上余维为q的最大叶状$C^r$-图册。

实践中，通常用较小的叶状图册表示叶状结构，通常还要求是规则的。

在图$U_i$中，条纹$x=\text{常数}$与别的图$U_j$上的条相匹配。这些子流形在图之间拼接成最大连通单射浸入子流形，就是叶状结构的叶（leaf）。 若缩小图$U_i$，可以写成$U_{ix}\times U_{iy}$，其中$U_{ix}\subset {ℝ}^{n-p},U_{iy}\subset {ℝ}^p.U_{}iy$与斑同构，$U_{ix}$的点参数化了$U_i$中的斑。若择$y_0\in U_{iy}$，则$U_{ix}\times \{y_0\}$是$U_i$的子流形，与每个斑恰交一次，这叫做叶状结构的局部横截面。注意，由于单值性的原因，全局横截面可能不存在。

r = 0的情形比较特殊。实践中出现的$C^0$叶状结构通常是“光滑叶”。更确切地说，是以下意义的$C^{r,0}$类：

定义 若叶状图册的相应相干类包含规则叶状图册$\{U_{\alpha },x_{\alpha },y_{\alpha }{\}}_{\alpha \in A}$，使得坐标变换式

$g_{\alpha \beta }(x_{\beta },y_{\beta })=(x_{\alpha }(x_{\beta },y_{\beta }),y_{\alpha }(y_{\beta })).$

属于$C^k$类，但$x_{\alpha }$在坐标$x_{\beta }$中是$C^r$类，其阶数≤ r、与$x_{\beta }$的混合偏导数在坐标$(x_{\beta },y_{\beta }$中是$C^k$类，则称叶状结构$ℱ$属于$C^{r,k}(r>k\ge 0)$类。

上述定义是所谓“叶状空间”的更一般概念。我们可以放宽横截的条件为${ℝ}^q$的相对紧开子集，允许横坐标$y_{\alpha }$在更一般的拓扑空间Z中取值。斑仍是${ℝ}^q$的相对紧开子集，横坐标公式$y_{\alpha }(y_{\beta })$的变化是连续的，$x_{\alpha }(x_{\beta },y_{\beta })$在坐标$x_{\beta }$中属于$C^r$类，其阶数 ≤ r 、与$x_{\beta }$的混合偏导数在坐标$(x_{\beta },y_{\beta })$中连续。一般要求M、Z为局部紧可测第二可数空间。这似乎是很狂野的推广，但在一些情形下很有用。

完整性

令$(M,ℱ)$是叶状流形（foliated manifold）。设L是$ℱ$的叶，s是L中的路径，我们感兴趣的是M中s的邻域中叶状结构的行为。直观地说，在叶上可以沿路径s行走，同时关注附近所有叶。在他（以下写作s(t)）行走时，一些叶可能会“掉落”、变得不可见；另一些可能会突然进入可视范围，渐渐接近L；还有些可能会以接近平行的方式跟随L，或垂直地打转之类。若s是环路，则随着t增大，s(t)会反复回到同一个点s(t₀)，每次都会有更多叶螺旋状地进入或离开视野。这种行为经过适当的形式化，叫做叶状结构的完整性（holonomy）。

完整性在叶状流形上有多种具体实现方式：叶状丛（foliated bundle）的总完整群、一般叶状流形的完整伪群、一般叶状流形的亏格完整广群、叶的亏格完整群、叶的无穷小完整群。

叶状丛

最容易理解的完整性是叶状丛的总完整性，这是庞加莱映射概念的推广。

横截面（cross section）N与第一回归映射（first return map）f，其中$M=S^1\times D^2,N=D^2.$

“第一回归映射”来自动力系统理论。令${\mathrm{\Phi }}_t$是紧n-流形上的非奇异$C^r(r\ge 1)$流。应用中，可以想象M是个回旋加速器或流体的闭合回路。若M有界，则假定流与界相切。流生成了1维叶状结构$ℱ$。若知道流的正方向，但不知道其他参数（轨迹形状、速度等），则称底叶状结构（underlying foliation）$ℱ$有向。假设流有全局横截面N，即N是M的n-1维紧正合嵌入的$C^r$子流形，叶状结构$ℱ$垂直于N，每条流线都与N相遇。由于N的维度与叶的维度是互补的，横截性条件是

$T_y(M)=T_y(ℱ)\oplus T_y(N)\text{ for each }y\in N.$

令$y\in N$，考虑M中所有序列${\{{\mathrm{\Phi }}_{t_k}(y)\}}_{k=1}^{\mathrm{\infty }}$的所有堆积点的ω-极限集合ω(y)，其中$t_k$为无穷大。可以证明，ω(y)是紧非空的，是流线的并。若$z=\underset{k\to \mathrm{\infty }}{\lim }{\mathrm{\Phi }}_{t_k}\in \omega (y),$则有值$t^{*}\in ℝ$使得${\mathrm{\Phi }}_{t^{*}}(z)\in N$，由此可得

$\underset{k\to \mathrm{\infty }}{\lim }{\mathrm{\Phi }}_{t_k+t^{\ast }}(y)={\mathrm{\Phi }}_{t^{\ast }}(z)\in N.$

由于N是紧的，$ℱ$横截于N，因此集合$\{t>0|{\mathrm{\Phi }}_t(y)\in N\}$是单调递增序列$\{{\tau }_k(y){\}}_{k=1}^{\mathrm{\infty }}$，并发散。

当$y\in N$变化，令$\tau (y)={\tau }_1(y)$，这样定义一个正函数$\tau \in C^r(N)$（第一回归时间），使得$\mathrm{\forall }y\in N,{\mathrm{\Phi }}_t(y)\notin N,0<t<\tau (y),{\mathrm{\Phi }}_{\tau (y)}(y)\in N.$

定义$f:N\to N,f(y)={\mathrm{\Phi }}_{\tau (y)}(y).$这是$C^r$映射。若流反向，则完全相同的构造会得到逆的$f^{-1}$；所以$f\in {\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}^r(N)$。这个微分同胚是第一回归映射，τ称作第一回归时间。虽然第一回归时间取决于流的参数化，但f显然只取决于有向叶状结构$ℱ$。可以将流${\mathrm{\Phi }}_t$重参数化，使其保持非奇异、是$C^r$类，且方向不翻转，从而使$\tau \equiv 1.$

流有横截面N的假设是很受限的，意味着M是$S^1$上纤维丛的总空间。事实上在$ℝ\times N$上，可将${\sim }_f$定义为以下条件生成的等价关系：

$(t,y){\sim }_f(t-1,f(y)).$

等价地，这是加法群Z在$ℝ\times N$上的作用的轨等价，定义如下

$\mathrm{\forall }k\in \mathbb{Z},\mathrm{\forall }(t,y)\in ℝ\times N,k\cdot (t,y)=(t-k,f^k(y)).$

f的映射圆柱定义为$C^r$流形

$M_f=(ℝ\times N)/{\sim }_f.$

由第一回归映射f的定义与第一回归时间$\tau \equiv 1$的假设，可立即得出映射

$\mathrm{\Phi }:ℝ\times N\to M.$

流的定义可诱导一个规范$C^r$微分同胚

$\phi :M_f\to M.$

若记$M_f=M$，则$ℝ\times N$到R的投影诱导了$C^r$映射

$\pi :M\to ℝ/\mathbb{Z}=S^1$

使M变为圆上纤维丛的总空间。这只是$S^1\times D^2$到$S^1$的投影。叶状结构$ℱ$横截于这丛的纤维，限制到每片叶L的丛投影π是覆盖映射$\pi :L\to S^1$，这就是叶状丛（foliated bundle）。

以$x_0\in S^1$的等价类$0+\mathbb{Z}$为基点，${\pi }^{-1}(x_0)$就是原横截面N。对$S^1$上以$x_0$为基点的每个环路s，同伦类$[s]\in {\pi }_1(S^1,x_0)$的唯一特征是$\mathrm{d}\mathrm{e}\mathrm{g}s\in \mathbb{Z}$。环路s提升到每条流线中的一条路径，很明显提升$s_y$始于$y\in N$、终于$f^k(y)\in N(k=\mathrm{d}\mathrm{e}\mathrm{g}s)$。微分同胚$f^k\in {\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}^r(N)$也用$h_s$表示，称作环路s的总整体性。由于只取决于[s]，因此定义了同胚

$h:{\pi }_1(S^1,x_0)\to {\mathrm{Diff}}^r(N),$

称作叶状丛的总整体同胚。

更直观地运用纤维丛，令$(M,ℱ)$是余维为q的叶状n-流形，令$\pi :M\to B$是纤维丛，具有q维纤维F与连通基空间B。假设所有这些结构都属于$C^r(0\le r\le \mathrm{\infty })$类，若r = 0，B支持一个$C^1$结构。由于B上的最大$C^1$图册都包含$C^{\mathrm{\infty }}$子图册，因此假设B如所期望那般光滑并不失一般性。最后，$\mathrm{\forall }x\in B$，假设x有连通开邻域$U\subseteq B$，和局部平凡化

$\begin{array}{ccc}{\pi }^{-1}(U)& \stackrel{\phi }{\to }& U\times F\\ \pi \downarrow & & \downarrow p\\ U& \stackrel{\text{id}}{\to }& U\end{array}$

其中φ是$C^r$微分同胚（若r = 0则是同胚），将$ℱ\mid {\pi }^{-1}(U)$带到积叶状结构$\{U\times \{y\}{\}}_{y\in F}$。其中，$ℱ\mid {\pi }^{-1}(U)$是叶为$L\cap {\pi }^{-1}(U)$的连通组分的叶状结构，L是$ℱ$的叶。这是$C^r$类“叶状丛”（foliated bundle）$(M,ℱ,\pi )$的一般定义。

$ℱ$垂直于π的纤维（可以说$ℱ$是垂直于纤维的），π到$ℱ$的每片叶L的限制是覆盖映射$\pi :L\to B$。特别是，每条纤维$F_x={\pi }^{-1}(x)$都与$ℱ$的每片叶相遇。纤维是$ℱ$的横截，与流的横截完全类似。

叶状结构$ℱ$横截于纤维不能保证叶是B的覆盖空间。这个问题的一个简单版本是${ℝ}^2$的一个叶状结构横截于纤维

$\pi :{ℝ}^2\to ℝ,$

$\pi (x,y)=x,$

但有无限多叶缺失了y轴。在相应的图像中，“有箭头的”叶以及它们上面所有的叶都渐进于x = 0轴。一般称这种叶状结构为相对于纤维是不完备的，即当参数$x\in B$接近某个$x_0\in B$，一些叶“奔向无穷大”。更确切地说，可能有叶L，和一条连续路径$s:[0,a)\to L$使得$\underset{t\to a-}{\lim }\pi (s(t))=x_0\in B$，但$\underset{t\to a-}{\lim }s(t)$在L的流形拓扑中不存在。这类似于不完备流，某些流线会在有限时间内发散。虽然这样的叶L可能在别处与${\pi }^{-1}(x_0)$相遇，但不能均匀覆盖$x_0$的邻域，因此不可能是B在π下的的覆盖空间。F是紧的时，$ℱ$对纤维的横截性确实保证了完备性，于是$(M,ℱ,\pi )$是叶状丛。

B上有图册$𝒰=\{U_{\alpha },x_{\alpha }{\}}_{\alpha \in A}$，包含开连通坐标图，以及平凡化${\phi }_{\alpha }:{\pi }^{-1}(U_{\alpha })\to U_{\alpha }\times F$，将$ℱ|{\pi }^{-1}(U_{\alpha })$带到积叶状结构。置$W_{\alpha }={\pi }^{-1}(U_{\alpha })$，并记${\phi }_{\alpha }=(x_{\alpha },y_{\alpha })$，其中（滥用符号）$x_{\alpha }$表示$x_{\alpha }\circ \pi ,y_{\alpha }:{\pi }^{-1}(U_{\alpha })\to F$是将${\phi }_{\alpha }$与规范投影$U_{\alpha }\times F\to F$组合而得的浸没。

图册$𝒲=\{W_{\alpha },x_{\alpha },y_{\alpha }{\}}_{\alpha \in A}$的作用类似叶状图册。$W_{\alpha }$的斑是$y_{\alpha }$的水平集，这一族斑通过$y_{\alpha }$，与F相同。由于预设了B支持某个$C^{\mathrm{\infty }}$结构，据怀特黑德定理，可在B上固定一个黎曼度量，择图册$𝒰$为测地凸的。于是，$U_{\alpha }\cap U_{\beta }$总是连通的。若这个交非空，则$W_{\alpha }$的每个斑都正好与$W_{\beta }$的一个斑相遇。然后，通过设下式，可定义一个完整上循环（holonomy cocycle）$\gamma ={\left\{{\gamma }_{\alpha \beta }\right\}}_{\alpha ,\beta \in A}$ by setting

${\gamma }_{\alpha \beta }=y_{\alpha }\circ y_{\beta }^{-1}:F\to F.$

例子

平坦空间

考虑n维空间，是由前n-p个坐标为常数的点组成的子空间之积。这可以用一张图（chart）表示，其基本原理是${ℝ}^n={ℝ}^{n-p}\times {ℝ}^p$，叶或斑${ℝ}^p$由${ℝ}^{n-p}$枚举。置n = 3、p = 2，可以类比三维空间：书的2维叶由（1维）页码枚举。

丛

较平凡的叶状结构例子是积$M=B\times F$，叶$F_b=\{b\}\times F,b\in B$（M的另一个叶状结构由$B_f=B\times \{f\},f\in F$给出）。

对流形F而言，$G=\mathrm{H}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{o}(F)$的平坦G-丛是更一般的一类。给定表示$\rho :{\pi }_1(B)\to \mathrm{H}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{o}(F)$，具有单值ρ的平坦$\mathrm{H}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{o}(F)$-丛由$M=(\tilde{B}\times F)/{\pi }_{1}B$给出，其中${\pi }_1(B)$通过甲板变换作用于万有覆盖$\tilde{B}$，通过表示ρ作用于F。

平坦丛符合纤维丛的框架。若有流形F使得$\mathrm{\forall }b\in B$，都有开邻域U使得有同胚$\phi :{\pi }^{-1}(U)\to U\times F(\pi =p_1\phi ,p_1:U\times F\to U)$（其中p₁是到第一个因子的投影），则流形之间的映射$\pi :M\to B$是纤维丛。纤维丛产生了由纤维$F_b:={\pi }^{-1}(\{b\}),b\in B$组成的叶状结构，其叶空间L与B同构，前者是豪斯多夫流形。

覆盖

若$M\to N$是流形间的覆盖映射，F是N上的叶状结构，则其拉回到M上的叶状结构。更一般地，若映射只是分歧覆盖（分歧轨迹横截于叶状结构），则叶状结构就可以被拉回。

浸没

若$M^n\to N^q,(q\le n)$是流形的浸没，则据反函数定理，浸没的纤维的连通组分定义了M的余维为q的叶状结构。纤维丛是这种类型的一个例子。

不是纤维丛的浸没的一个例子是

$\{\begin{array}{c}f:[-1,1]\times ℝ\to ℝ\\ f(x,y)=(x^2-1)e^y\end{array}$

这种浸没产生了$[-1,1]\times ℝ$的叶状结构，在下列$\mathbb{Z}$作用下是不变的：

$z(x,y)=(x,y+n),\text{or}z(x,y)=((-1{)}^{n}x,y)$

其中$(x,y)\in [-1,1]\times ℝ,n\in \mathbb{Z}$。$\mathbb{Z}\mathrm{\setminus }([-1,1]\times ℝ)$的诱导叶状结构称作（环空的）2维里布叶状结构，或（莫比乌斯带的）2维无向里布叶状结构。它们的叶空间都不是豪斯多夫的。

里布叶状结构

定义一个潜没

$\{\begin{array}{c}f:D^n\times ℝ\to ℝ\\ f(r,\theta ,t):=(r^2-1)e^t\end{array}$

其中$(r,\theta )\in [0,1]\times S^{n-1}$是n维圆盘$D^n$上的圆柱坐标。这浸没产生了$D^n\times ℝ$的叶状结构，在如下Z作用下是不变的：

$z(x,y)=(x,y+z)((x,y)\in D^n\times ℝ,z\in \mathbb{Z})$

$\mathbb{Z}\mathrm{\setminus }(D^n\times ℝ)$的诱导叶状结构被称作n维里布叶状结构，其叶空间不是豪斯多夫的。

对于n = 2，这给出了实心环面的叶状结构，可由沿边界粘合两个实心环面，来定义3-球的里布叶状结构。奇数维球$S^{2n+1}$的叶状结构也是明确已知的。

李群

若G是李群、H是李子群，则G就会被H的陪集叶化。若H在G中闭合，则商空间$G/H$是光滑（豪斯多夫）流形，将G转化为纤维丛，纤维H、基为$G/H$。这个纤维丛实际上是主的，具有结构群H。

李群作用

令G是光滑作用于流形M的李群。若作用是局部自由作用或自由作用，则G的轨道定义了M的一个叶状结构。

线性叶状结构与克罗内克叶状结构

若$\tilde{X}$是非奇异（即无处为零）的向量场，则$\tilde{X}$定义的局部流拼凑在一起，就定义了维度为1的叶状结构。事实上，给定任一点$x\in M$，由于$\tilde{X}$是非奇异的，所以可找到一个关于x的坐标邻域$(U,x^1,,\dots ,x^n)$，使得

$-\epsilon <x^i<\epsilon ,1\le i\le n,$

$\frac{\partial }{\partial x^1}=\tilde{X}\mid U.$

从几何角度来看，$\tilde{X}\mid U$的流线就是水平集

$x^i=c^i,2\le i\le n,$

其中所有的$|c^i|<\epsilon .$由惯例，流形是第二可数的，因此类似“长线”这样的叶异常现象会被M本身的第二可数性排除。要求$\tilde{X}$是完全域（例如M是紧的），从而要求每片叶都是流线，就可以避开这个难题。

${ℝ}^2$上的线性叶状结构$\widetilde{ℱ}$传递到$T^2$上的叶状结构$ℱ$。 a) 斜率是有理的（线性叶状结构）； b) 斜率是无理的（克罗内克叶状结构）。

2-环面上的无理旋转

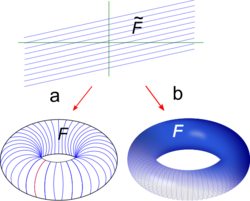
环面$T^2$上的一类重要1维叶状结构来自投影于其上的恒向量场。${ℝ}^2$上的恒向量场

$\tilde{X}\equiv \left[\begin{array}{c}a\\ b\end{array}\right]$

对${ℝ}^2$中所有平移都不变，因此当投影到环面$T^2={ℝ}^2/{\mathbb{Z}}^2$时传递到良定义向量场X。假定a ≠ 0。$\tilde{X}$产生的${ℝ}^2$上的叶状结构$\widetilde{ℱ}$的叶具有斜率为$\theta =b/a$的平行线，这叶状结构在平移下也是不变的，并传递到X产生的$T^2$上的叶状结构$ℱ$。

$\widetilde{ℱ}$每片叶的形式是

$\tilde{L}=\{(x_0+ta,y_0+tb){\}}_{t\in ℝ}.$

若斜率是有理的，则所有叶都是与圆同胚的闭合曲线。这时，可取$a,b\in \mathbb{Z}$。对固定的$t\in ℝ$，$\tilde{L}$中与$t\in t_0+\mathbb{Z}$的值对应的点都投影到$T^2$的同一点，于是$ℱ$对应的叶L是$T^2$中的嵌入圆。由于L是任意的，所以$ℱ$是$T^2$对圆的叶状结构。由此很容易得出，这个叶状结构实际上就是纤维丛$\pi :T^2\to S^1$，这就是所谓线性叶状结构。

若斜率是无理的，则叶是非紧的，同胚于非紧实线，在环面中稠密（参无理旋转）。每个点$(x_0,y_0)$的轨迹永远不会回到同一点，而是在环面上产生“处处稠密”的环绕，会任意接近任何给定的点。于是，轨迹的闭包是整个2维环面。这种情形称作克罗内克叶状结构，得名于利奥波德·克罗内克与

克罗内克稠密性定理 若实数θ不等于π的所有有理倍数，则集合$\{e^{in\theta }|n\in \mathbb{Z}\}$在单位圆内稠密。

证明

首先注意，若$\widetilde{ℱ}$的叶$\tilde{L}$不是一一投影到$T^2$，则一定有实数$t\ne 0$使得ta、tb都是整数。但这意味着$b/a\in \mathbb{Q}$。要证$ℱ$的叶L在$T^2$中都稠密，只需证明$\mathrm{\forall }v\in {ℝ}^2$，$\widetilde{ℱ}$的每片叶$\tilde{L}$与陪集$v+{\mathbb{Z}}^2$中的适当点间距都是任意小的正距离。${ℝ}^2$中的适当平移使我们可以假设v = 0，这样任务就简化为证明$\tilde{L}$任意地经过合适的点$(n,m)\in {\mathbb{Z}}^2$。线$\tilde{L}$具有斜截式 $y=\theta x+c.$ 因此，对于任意$\eta >0$，只要找到整数n、m使得 $|\theta n+c-m|<\eta .$ 等价地，$c\in ℝ$是任意的，就可以证明集合$\{\theta n-m{\}}_{m,n\in \mathbb{Z}}$在R中稠密。这实质上就是欧多克索斯关于θ与1不可通约（即θ无理）的标准。

用平行线对${ℝ}^n$进行叶状结构的类似构造，可得与环面上的线性流相关的n-环面${ℝ}^n/{\mathbb{Z}}^n$的1维叶状结构。

纬悬叶状结构

平坦丛不仅有对纤维的线性结构，还有横截于纤维的叶状结构，其叶为

$L_f:=\{p(\tilde{b},f):\tilde{b}\in \tilde{B}\},\text{ for }f\in F,$

其中$p:\tilde{B}\times F\to M$是规范投影。这个叶状结构称作表示$\rho :{\pi }_1(B)\to \mathrm{H}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{o}(F)$的纬悬。

具体地说，若$B=S^1$，$\phi :F\to F$是F的同胚，则$\phi$的纬悬叶状结构定义为表示$\rho :\mathbb{Z}\to \mathrm{H}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{o}(F)$的纬悬叶状结构，由$\rho (z)={\mathrm{\Phi }}^z$给出。其叶空间是$L=ℱ/\sim$，其中只要对某个$n\in \mathbb{Z},y={\mathrm{\Phi }}^n(x),x\sim y$。

纬悬叶状结构最简单的例子是q维流形X。令$f:X\to X$是双射。将纬悬$M=S^1{\times }_{f}X$定义为$[0,1]\times X$对等价关系$(1,x)\sim (0,f(x))$的商。

$M=S^1{\times }_{f}X=[0,1]\times X$

则，M自动携带两个叶状结构：${ℱ}_2$包含$F_{2,t}=\{(t,x{)}_{\sim }:x\in X\}$形式的集合；${ℱ}_1$包含$F_{2,x_0}=\{(t,x):t\in [0,1],x\in O_{x_0}\}$形式的集合，其中轨道$O_{x_0}$定义为

$O_{x_0}=\{\dots ,f^{-2}(x_0),f^{-1}(x_0),x_0,f(x_0),f^2(x_0),\dots \}$

其中指数指的是函数f与自身复合的次数。注意$O_{x_0}=O_{f(x_0)}=O_{f^{-2}(x_0)},\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{.}$，对$F_{1,x_0}$也同样。理解叶状结构${ℱ}_1$等效于理解映射f的动力学。若流形X已经叶化，则只要f是叶间映射，就可以利用这构造增加叶状结构的余维数。

2-环面的克罗内克叶状结构是旋转$R_{\alpha }:S^1\to S^1$（角度为$\alpha \in [0,2\pi )$）的纬悬叶状结构。

切割重粘后，2-洞环面的纬悬。 a) 带待切割截面的双洞环面； b) 切割后带有4个面的几何图形。

更具体地说，若$\mathrm{\Sigma }={\mathrm{\Sigma }}_2$是2洞环面，$C^1,C^2\in \mathrm{\Sigma }$是两个嵌入圆，则$ℱ$是叶$\mathrm{\Sigma }\times \{y\},y\in S^1$的3-流形的积叶状结构$M=\mathrm{\Sigma }\times S^1$。注意$N_i=C_i\times S^1$是嵌入环，$ℱ$横截于$N_i,i=1,2$。令${\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}_{+}(S^1)$表示$S^1$的保向微分同胚群，并择$f_1,f_2\in {\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}_{+}(S^1)$。将M沿$N_1,N_2$切开，$N_i^{+},N_i^{-}$表示它们的副本。这时，流形$M^{\prime }={\mathrm{\Sigma }}^{\prime }\times S_1$有4个边界分量${\left\{N_i^{\pm }\right\}}_{i=1,2}.$叶状结构$ℱ$横截边界$\partial M^{\prime }$的叶状结构${ℱ}^{\mathcal{\prime }}$，叶的形式为${\mathrm{\Sigma }}^{\prime }\times \{y\},y\in S^1$。

这片叶在4个圆$C_i^{\pm }\times \{y\}\subset N_i^{\pm }$中与$\partial M^{\prime }$相遇。若$z\in C_i$，则$C_i^{\pm }$中的对应点记作$z^{\pm }$，$N_i^{-}$通过下列标识，“回到”$N_i^{+}$：

$(z^{-},y)\equiv (z^{+},f_i(y)),i=1,2.$

由于$f_1,f_2$是$S^1$的保向微分同胚，因此与恒同（identity）同痕，由这操作得到的流形同胚于M。${ℱ}^{\mathcal{\prime }}$的叶则重新组合，产生M新的叶状结构$ℱ(f_1,f_2)$。若$ℱ(f_1,f_2)$的叶L 包含一片${\mathrm{\Sigma }}^{\prime }\times \{y_0\}$，则

$L=\bigcup _{g\in G}{\mathrm{\Sigma }}^{\prime }\times \{g(y_0)\},$

其中$G\subset {\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}_{+}(S^1)$是由$\{f_1,f_2\}$生成的子群。这些Σ'的副本通过标识彼此相连：

$\mathrm{\forall }z\in C_1,(z^{-},g(y_0))\equiv (z^{+},f_1(g(y_0)))$

$\mathrm{\forall }z\in C_2,(z^{-},g(y_0))\equiv (z^{+},f_2(g(y_0)))$

其中g在G上取值。叶完全由$y_0\in S^1$的G-轨道决定，可以很简单也可以很复杂。例如若相应的G-轨道有限，则叶就是紧的。举个极端的例子，若G是平凡的$(f_1=f_2={\mathrm{i}\mathrm{d}}_{S^1})$，则$ℱ(f_1,f_2)=ℱ$。若轨道在$S^1$中是稠密的，则对应的叶在M中也稠密。例如，若$f_1,f_2$是2π的有理独立倍的旋转，则每片叶都是稠密的。其他例子中，某些叶L的闭包$\overline{L}$与每个因子$\{w\}\times S^1$在康托尔集中相遇。在$\mathrm{\Sigma }\times I$上也可做类似构造，其中I是紧非退化区间。这里，取$f_1,f_2\in {\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}}_{+}(I)$，由于$\partial I$通过所有保向微分同胚逐点固定了，所以可得一个以$\partial M$的两分量为叶的叶状结构。若在这情形下形成M' ，就会得到有角叶状流形。无论哪种情形，这种构造都被称作微分同胚对的纬悬，提供了余维为1的叶状结构的有趣例子。

叶状结构与可积性

假设一切都光滑，那么向量场之间有一种密切关系：给定M上不为零的向量场X，其积分曲线将给出1维叶状结构（即余维为n-1的叶状结构）。

这观察可推广为弗罗贝尼乌斯定理，即分布（流形切丛的n − p维子丛）与叶状结构的叶相切的充分必要条件是，与分布相切的向量场集对李括号闭合。这也可以解释为，将切丛的结构群从$\mathrm{G}\mathrm{L}(n)$约化为可约群。

弗罗贝尼乌斯定理中的条件作为可积条件出现，并断言若满足条件，就能约化，因为具有所需块结构的局部转移函数存在。例如，对某（非规范）$\alpha \in {\mathrm{\Omega }}^1$（即非零余向量场），余维为1时可定义叶状结构的切丛为$\mathrm{k}\mathrm{e}\mathrm{r}(\alpha )$。若处处都有$\alpha \wedge \mathrm{d}\alpha =0$，则给定的α可积。

由于存在拓扑约束，因此存在全局叶状结构理论。例如，曲面情形中，处处非零向量场只能存在于环面的有向紧曲面上。这是庞加莱-霍普夫定理的结果，指出欧拉示性数需为0。其与切触几何有很多深层联系，专门研究不可积情形。

叶状结构的存在

Template:Harvtxt给出连通非紧流形上的分布与可积分布同伦的充分必要条件。Template:Harvs证明，任意有分布的紧流形都有同维度的叶状结构。

参看

• 弗罗贝尼乌斯定理
• G结构
• 用叶状结构分类空间
• 里布叶状结构
• 紧叶状结构(Taut foliation)

参考文献

• Template:Eom
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Citation
• Template:Citation
• Template:Citation
• Template:Citation
• Template:CitationTemplate:Dead link
• Template:Citation

外部链接

• Foliations Template:Wayback at the Manifold Atlas