Γ函数

Γ函數在实数定义域上的函數圖形

Template:微積分學 在數學中，$\mathrm{\Gamma }$函数（伽瑪函數；Gamma函数），是階乘函數在實數與複數域上的擴展。如果$n$為正整數，則：

$\mathrm{\Gamma }(n)=(n-1)!$

根据解析延拓原理，伽瑪函數可以定義在除去非正整數的整個複數域上：

$\mathrm{\Gamma }(z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{z-1}{\mathrm{e}}^{-t}\mathrm{d}\mathrm{t},$ $\mathrm{\Re }(z)>0.$

数学家勒讓德首次使用了希腊字母Γ作为该函数的记号。在機率論和组合数学中此函數很常用。

定義

$\mathrm{\Gamma }$函數可以通过欧拉（Euler）第二类积分定義：

$\mathrm{\Gamma }(z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{z-1}{\mathrm{e}}^{-t}\mathrm{d}\mathrm{t}$

对复数$z$，我们要求$\mathrm{R}\mathrm{e}(z)>0$。

$\mathrm{\Gamma }$函數还可以通过对${\mathrm{e}}^{-t}$做泰勒展开，解析延拓到整个复平面： $\mathrm{\Gamma }(z)=\underset{1}{\overset{\mathrm{\infty }}{\int }}\frac{t^{z-1}}{{\mathrm{e}}^t}\mathrm{d}t+\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{n!}\frac{1}{n+z}$

这样定义的$\mathrm{\Gamma }$函數在全平面除了$z=0,-1,-2,\dots$以外的地方解析。

$\mathrm{\Gamma }$函數也可以用无穷乘积的方式表示：

$\mathrm{\Gamma }(z)=\frac{1}{z}\prod _{n=1}^{\mathrm{\infty }}{(1+\frac{z}{n})}^{-1}{(1+\frac{1}{n})}^z$

这说明$\mathrm{\Gamma }(z)$是亚纯函数，而$\frac{1}{\mathrm{\Gamma }(z)}$是全纯函数。

历史動機

Γ函數本身可以被看作是一個下列插值問題的解：

『找到一個光滑曲線連接那些由 $y=(x-1)!$ 所給定的點$(x,y)$，並要求$x$要為正整數』

由前幾個的階乘清楚地表明這樣的曲線是可以被畫出來的，但是我們更希望有一個精確的公式去描述這個曲線，並讓階乘的操作不會依賴於$x$值的大小。而最簡單的階乘公式 $x!=1\times 2\times \cdots \times x$ 不能直接應用在$x$值為分数的時候，因為它被限定在$x$值為正整數而已。相對而言，并不存在一個有限的關於加總、乘積、冪次、指數函數或是對數函數可以表達 $x!$，但是是有一個普遍的公式藉由微積分的積分與極限去表達階乘的，而 Γ函數就是那個公式。

階乘有無限多種的連續擴張方式將定義域擴張到非整數：可以通過任何一組孤立點畫出無限多的曲線。Γ函數是實務上最好的一個選擇，因為是解析的(除了非正整數點)，而且它可以被定義成很多種等價形式。然而，它並不是唯一一個擴張階乘意義的解析函數，只要給予任何解析函數，其在正整數上為零，像是 $k\sin (m\pi x)$，會給出其他函數有著階乘性質。

無窮乘積

$\mathrm{\Gamma }$函數可以用無窮乘積表示：

$\mathrm{\Gamma }(z)=\underset{n\to \mathrm{\infty }}{\lim }n!n^z\prod _{k=0}^n(z+k{)}^{-1}$

$\mathrm{\Gamma }(z)=\frac{{\mathrm{e}}^{-\gamma z}}{z}\prod _{n=1}^{\mathrm{\infty }}{(1+\frac{z}{n})}^{-1}{\mathrm{e}}^{\frac{z}{n}}$

其中$\gamma$是欧拉-马歇罗尼常数。

Γ積分

$1=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{x^{\alpha -1}{\lambda }^{\alpha }{\mathrm{e}}^{-\lambda x}}{\mathrm{\Gamma }\left(\alpha \right)}\mathrm{d}x$

$⟹\frac{\mathrm{\Gamma }\left(\alpha \right)}{{\lambda }^{\alpha }}=\underset{0}{\overset{\mathrm{\infty }}{\int }}{x}^{\alpha -1}{\mathrm{e}}^{-\lambda x}\mathrm{d}x$

递推公式

$\mathrm{\Gamma }$函数的递推公式为： $\mathrm{\Gamma }(x+1)=x\mathrm{\Gamma }(x)$，

对于正整数$n$，有

$\mathrm{\Gamma }(n+1)=n!$，

可以说$\mathrm{\Gamma }$函数是階乘的推廣。

递推公式的推导

$\mathrm{\Gamma }(n+1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{\mathrm{e}}^{-x}{x}^{n+1-1}\mathrm{d}x=\underset{0}{\overset{\mathrm{\infty }}{\int }}{\mathrm{e}}^{-x}{x}^n\mathrm{d}x$

我们用分部积分法来计算这个积分：

$\underset{0}{\overset{\mathrm{\infty }}{\int }}{\mathrm{e}}^{-x}{x}^n\mathrm{d}x={\left[\frac{-x^n}{{\mathrm{e}}^x}\right]}_0^{\mathrm{\infty }}+n\underset{0}{\overset{\mathrm{\infty }}{\int }}{\mathrm{e}}^{-x}{x}^{n-1}\mathrm{d}x$

当$x=0$时，$\frac{-0^n}{{\mathrm{e}}^0}=\frac{0}{1}=0$。当$x$趋于无穷大时，根据洛必达法则，有：

$\underset{x\to \mathrm{\infty }}{\lim }\frac{-x^n}{{\mathrm{e}}^x}=\underset{x\to \mathrm{\infty }}{\lim }\frac{-n!\cdot 0}{{\mathrm{e}}^x}=0$.

因此第一项${\left[\frac{-x^n}{{\mathrm{e}}^x}\right]}_0^{\mathrm{\infty }}$变成了零，所以：

$\mathrm{\Gamma }(n+1)=n\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{x^{n-1}}{{\mathrm{e}}^x}\mathrm{d}x$

等式的右面正好是$n\mathrm{\Gamma }(n)$, 因此，递推公式为：

$\mathrm{\Gamma }(n+1)=n\mathrm{\Gamma }(n)$.

重要性质

• 當$z\to 0^{+}$時，$\mathrm{\Gamma }(z)\to +\mathrm{\infty }$
• 歐拉反射公式（余元公式）：

$\mathrm{\Gamma }(z)\mathrm{\Gamma }(1-z)=\frac{\pi }{\sin \pi z}(0<\mathrm{R}\mathrm{e}(z)<1)$.

由此可知当$z=\frac{1}{2}$时，$\mathrm{\Gamma }\left(\frac{1}{2}\right)=\sqrt{\pi }$.

• 伽马函数还是负自然指数函数的梅林变换: $\mathrm{\Gamma }(z)=ℳ\{e^{-x}\}(z).$

• 乘法定理：

$\mathrm{\Gamma }(z)\mathrm{\Gamma }(z+\frac{1}{2})=2^{1-2z}\sqrt{\pi }\mathrm{\Gamma }(2z)$。

$\mathrm{\Gamma }(z)\mathrm{\Gamma }(z+\frac{1}{m})\mathrm{\Gamma }(z+\frac{2}{m})\cdots \mathrm{\Gamma }(z+\frac{m-1}{m})=(2\pi {)}^{\frac{m-1}{2}}{m}^{\frac{1}{2}-mz}\mathrm{\Gamma }(mz)$.

• 此外：

$\mathrm{\Gamma }(n+\frac{1}{2})=\frac{(2n)!\sqrt{\pi }}{n!4^n}$.

• 使用乘法定理推導的關係：

$\mathrm{\Gamma }(1/6)=\mathrm{\Gamma }(1/3{)}^2/\sqrt{\pi }*2^{2/3}*\sin (\pi /3).$

$\mathrm{\Gamma }(5/6)=1/\mathrm{\Gamma }(1/3{)}^2*{\sqrt{\pi }}^3*2^{4/3}/\sqrt{3}.$

$\mathrm{\Gamma }(1/10)=\mathrm{\Gamma }(1/5)*\mathrm{\Gamma }(2/5)/\sqrt{\pi }*2^{4/5}*\sin (2*\pi /5).$

$\mathrm{\Gamma }(3/10)=\mathrm{\Gamma }(1/5)/\mathrm{\Gamma }(2/5)*\sqrt{\pi }/2^{3/5}/\sin (3*\pi /10).$

$\mathrm{\Gamma }(7/10)=\mathrm{\Gamma }(2/5)/\mathrm{\Gamma }(1/5)*\sqrt{\pi }*2^{3/5}.$

$\mathrm{\Gamma }(9/10)=1/(\mathrm{\Gamma }(1/5)*\mathrm{\Gamma }(2/5))*{\sqrt{\pi }}^3/2^{4/5}/(\sin (\pi /10)*\sin (2*\pi /5)).$

此式可用來協助計算t分布機率密度函數、卡方分布機率密度函數、F分布機率密度函數等的累計機率。

• 極限性質

對任何實數α

$\underset{n\to \mathrm{\infty }}{\lim }\frac{\mathrm{\Gamma }(n+\alpha )}{\mathrm{\Gamma }(n)n^{\alpha }}=1,\alpha \in 𝐑$

斯特靈公式

Template:函數圖形 Template:Main 斯特靈公式能用以估計$\mathrm{\Gamma }(z)$函数的增長速度。公式為：

$\mathrm{\Gamma }(z+1)\sim \sqrt{2\pi z}{\left(\frac{z}{e}\right)}^z,$

其中e約等於Template:複變運算。

特殊值

$\begin{array}{ccccc}\mathrm{\Gamma }(-\frac{3}{2})& =& \frac{4}{3}\sqrt{\pi }& \approx & 2.363271801207\\ \mathrm{\Gamma }(-\frac{1}{2})& =& -2\sqrt{\pi }& \approx & -3.544907701811\\ \mathrm{\Gamma }\left(\frac{1}{2}\right)& =& \sqrt{\pi }& \approx & 1.772453850906\\ \mathrm{\Gamma }(1)& =& 0!& =& 1\\ \mathrm{\Gamma }\left(\frac{3}{2}\right)& =& \frac{1}{2}\sqrt{\pi }& \approx & 0.886226925453\\ \mathrm{\Gamma }(2)& =& 1!& =& 1\\ \mathrm{\Gamma }\left(\frac{5}{2}\right)& =& \frac{3}{4}\sqrt{\pi }& \approx & 1.329340388179\\ \mathrm{\Gamma }(3)& =& 2!& =& 2\\ \mathrm{\Gamma }\left(\frac{7}{2}\right)& =& \frac{15}{8}\sqrt{\pi }& \approx & 3.323350970448\\ \mathrm{\Gamma }(4)& =& 3!& =& 6\end{array}$

连分数表示

伽马函数也可以在复数域表示为两个连分数之和：

$\mathrm{\Gamma }(z)=\frac{e^{-1}}{2+0-z+1\frac{z-1}{2+2-z+2\frac{z-2}{2+4-z+3\frac{z-3}{2+6-z+4\frac{z-4}{2+8-z+5\frac{z-5}{2+10-z+\ddots }}}}}}+\frac{e^{-1}}{z+0-\frac{z+0}{z+1+\frac{1}{z+2-\frac{z+1}{z+3+\frac{2}{z+4-\frac{z+2}{z+5+\frac{3}{z+6-\ddots }}}}}}}$

导数

Template:函數圖形 對任何複數z，滿足 Re(z) > 0，有

$\frac{{\mathrm{d}}^n}{\mathrm{d}{z}^n}\mathrm{\Gamma }(z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{z-1}{e}^{-t}(\ln t{)}^{n}dt$

於是，對任何正整數 m

${\mathrm{\Gamma }}^{\prime }(m+1)=m!(-\gamma +\sum _{k=1}^m\frac{1}{k})$

其中γ是歐拉-馬歇羅尼常數。

复数值

$\mathrm{\Gamma }(x+\mathrm{i}y)=\{\underset{1}{\overset{\mathrm{\infty }}{\int }}\frac{t^{x-1}}{{\mathrm{e}}^t}\cos (y\ln t)\mathrm{d}t+\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{k!}\left[\frac{k+x}{(k+x{)}^2+y^2}\right]\}+\mathrm{i}\{\underset{1}{\overset{\mathrm{\infty }}{\int }}\frac{t^{x-1}}{{\mathrm{e}}^t}\sin (y\ln t)\mathrm{d}t-\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{k!}\left[\frac{y}{(k+x{)}^2+y^2}\right]\}$

解析延拓

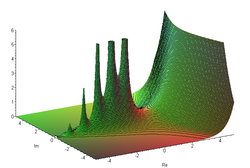Γ函數的絕對值函數圖形

注意到在$\mathrm{\Gamma }$函數的積分定義中若取$z$為實部大於零之複數、則積分存在，而且在右半複平面上定義一個全純函數。利用函數方程

$\mathrm{\Gamma }(z)\mathrm{\Gamma }(1-z)=\frac{\pi }{\sin \pi z}(0<\mathrm{R}\mathrm{e}(z)<1)$

並注意到函數$\sin (\pi z)$在整個複平面上有解析延拓，我們可以在$\mathrm{R}\mathrm{e}(z)<1$時設

$\mathrm{\Gamma }(z)=\frac{\pi }{\mathrm{\Gamma }(1-z)\sin \pi z}$

從而將$\mathrm{\Gamma }$函數延拓為整個複平面上的亞純函數，它在$z=0,-1,-2,-3\cdots$有單極點，留數為

$\mathrm{R}\mathrm{e}\mathrm{s}(\mathrm{\Gamma },-n)=\frac{(-1{)}^n}{n!}.$

程式實現

許多程式語言或試算表軟體有提供Γ函数或對數的Γ函数，例如EXCEL。而對數的Γ函数還要再取一次自然指數才能獲得Γ函数值。例如在EXCEL中，可使用GAMMALN函数，再用EXP[GAMMALN(X)]，即可求得任意實数的伽玛函数的值。

• 例如在EXCEL中：EXP[GAMMALN(4/3)]=Template:複變運算

而在沒有提供Γ函数的程式環境中，也能夠過泰勒級數或斯特靈公式等方式來近似，例如Robert H. Windschitl在2002年提出的方法，其在十進制可獲得有效數-{}-字八位數的精確度，已足以填滿單精度浮點數的二進制有效數-{}-字24位：

$\mathrm{\Gamma }(z)\approx \sqrt{\frac{2\pi }{z}}{\left(\frac{z}{e}\sqrt{z\sinh \frac{1}{z}+\frac{1}{810z^6}}\right)}^z$

参见

• 双伽玛函数
• 多伽玛函数
• 倒數伽瑪函數
• 反伽瑪函數
• 伽玛分布

外部链接

• 神奇的Gamma函数(上)
• 神奇的Gamma函数(下)