遞迴最小平方濾波器

Template:NoteTA 遞迴最小平方濾波器（RLS）屬於自适应滤波器，會針對和輸入信號有關的Template:Link-en损失函数，遞迴尋找可以使其最小化的係數。此方法和想要減少均方误差的最小均方滤波器（LMS）不同。在推導遞迴最小平方濾波器時，會假設輸入信號是确定性的，而最小均方滤波及其他演算法會假設信號Template:Link-en。和其他的方法比較起來，遞迴最小平方濾波器的收斂速度特別快。但其代價是非常高的運算複雜度。

演進

遞迴最小平方濾波器是由卡爾·弗里德里希·高斯發現，但被遺忘無人使用，直到Plackett在1950年發現高斯1821年的著作之後，才再獲使用。一般來說，遞迴最小平方濾波器可以求得任何可以用自适应滤波器求解的問題。例如，假設信號$d(n)$從有回聲的有噪信道傳輸，接收到的是

$x(n)=\sum _{k=0}^q{b}_n(k)d(n-k)+v(n)$

其中$v(n)$代表加性高斯白噪声。RLS濾波器的目的是用$p+1$階有限冲激响应（FIR）濾波器$𝐰$，還原想要的訊號$d(n)$：

$d(n)\approx \sum _{k=0}^{p}w(k)x(n-k)={𝐰}^{𝑇}{𝐱}_n$

其中${𝐱}_n=[x(n)x(n-1)\dots x(n-p){]}^T$是包括$x(n)$最近$p+1$次取樣的-{zh-tw:行; zh-cn:列;}-向量。接收到想要訊號的估測值為

$\hat{d}(n)=\sum _{k=0}^p{w}_n(k)x(n-k)={𝐰}_n^{𝑇}{𝐱}_n$

其目的是估測濾波器$𝐰$的參數，在每個時間$n$，會將目前的估測值用${𝐰}_n$表示，自適應的最小方差估測值為${𝐰}_{n+1}$。${𝐰}_n$也是如下的列向量，其转置${𝐰}_n^{𝑇}$則是-{zh-tw:列; zh-cn:行;}-向量。矩陣乘法${𝐰}_n^{𝑇}{𝐱}_n$（也是${𝐰}_n$和${𝐱}_n$的點積）是$\hat{d}(n)$為純量。若$\hat{d}(n)-d(n)$在最小二乘法的概念下，其值是小的，其估測就算是好的。

隨著時間演進，會希望避免完全重做最小方差演算法來找新估測值${𝐰}_{n+1}$，會希望可以將新估測值${𝐰}_{n+1}$用${𝐰}_n$配合其他變數來表示。

遞迴最小平方濾波器的好處是不用進行反矩陣運算，因此可以節省計算時間。另一個好處是在其結果之後，提供了類似卡尔曼滤波的直覺資訊。

概念

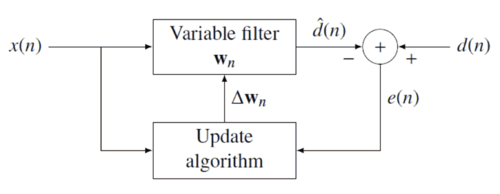
遞迴最小平方濾波器背後的概念是在收到新資料時，適當選擇濾波器係數${𝐰}_n$、更新濾波器，以及讓损失函数 $C$最小化。誤差信號$e(n)$和期望信號$d(n)$之間的關係，可以用以下的负反馈方塊圖來說明：

誤差會透過估測值$\hat{d}(n)$，受到濾波器係數影響：

$e(n)=d(n)-\hat{d}(n)$

加權最小方差函數$C$—希望可以最小化的費用函數—是$e(n)$的函數，因此也會受到濾波器係數的影響：

$C({𝐰}_n)=\sum _{i=0}^n{\lambda }^{n-i}{e}^2(i)$

其中$0<\lambda \le 1$，是「遺忘因子」（forgetting factor），以指數的方式讓較舊的資料有較小的加權。

費用函數最小化的方式，是將係數向量${𝐰}_n$中的所有項次微分，並讓微分為零

$\frac{\partial C({𝐰}_n)}{\partial w_n(k)}=\sum _{i=0}^{n}2{\lambda }^{n-i}e(i)\cdot \frac{\partial e(i)}{\partial w_n(k)}=-\sum _{i=0}^{n}2{\lambda }^{n-i}e(i)x(i-k)=0k=0,1,\dots ,p$

接著，用以下的誤差信號來代替$e(n)$

$\sum _{i=0}^n{\lambda }^{n-i}[d(i)-\sum _{\ell =0}^p{w}_n(\ell )x(i-\ell )]x(i-k)=0k=0,1,\dots ,p$

將等式重組如下

$\sum _{\ell =0}^p{w}_n(\ell )[\sum _{i=0}^n{\lambda }^{n-i}x(i-\ell )x(i-k)]=\sum _{i=0}^n{\lambda }^{n-i}d(i)x(i-k)k=0,1,\dots ,p$

可以表示為以下的矩陣

${𝐑}_x(n){𝐰}_n={𝐫}_{dx}(n)$

其中${𝐑}_x(n)$是$x(n)$的加權Template:Link-en矩陣，而${𝐫}_{dx}(n)$是$d(n)$和$x(n)$互协方差的等效估計。依照上式可以找到最小化費用函數的係數

${𝐰}_n={𝐑}_x^{-1}(n){𝐫}_{dx}(n)$

如何選擇λ

$\lambda$越小，舊數據對協方差矩陣的影響越小，讓濾波器對最近的數據較敏感，這也會讓濾波器的co-efficients比較容易振盪。$\lambda =1$稱為growing window遞迴最小平方演算法。在實務上，會讓$\lambda$0.98介於1之間。利用第二型的最大可能區間估測，可以用資料中估測到最佳的$\lambda$。

遞迴演算法

以上敘述的結論是可以決定費用函數的參數，使費用函數最小化的方程式。以下則說明如何找到此形式的遞迴解

${𝐰}_n={𝐰}_{n-1}+\mathrm{\Delta }{𝐰}_{n-1}$

其中$\mathrm{\Delta }{𝐰}_{n-1}$是時間$n-1$的修正因子。首先將互協方差${𝐫}_{dx}(n)$用${𝐫}_{dx}(n-1)$來表示

${𝐫}_{dx}(n)$	$=\sum _{i=0}^n{\lambda }^{n-i}d(i)𝐱(i)$
	$=\sum _{i=0}^{n-1}{\lambda }^{n-i}d(i)𝐱(i)+{\lambda }^{0}d(n)𝐱(n)$
	$=\lambda {𝐫}_{dx}(n-1)+d(n)𝐱(n)$

其中$𝐱(i)$是$p+1$維的資料向量

$𝐱(i)=[x(i),x(i-1),\dots ,x(i-p){]}^T$

接下來以相似的方式，用${𝐑}_x(n-1)$表示${𝐑}_x(n)$

${𝐑}_x(n)$	$=\sum _{i=0}^n{\lambda }^{n-i}𝐱(i){𝐱}^T(i)$
	$=\lambda {𝐑}_x(n-1)+𝐱(n){𝐱}^T(n)$

為了要找到其係數向量，接下來要關注的是決定性自協方差矩陣的反矩陣。這問題可以使用Template:Link-en。若

$A$	$=\lambda {𝐑}_x(n-1)$ 是 $(p+1)\times (p+1)$矩陣
$U$	$=𝐱(n)$ 是 $(p+1)\times 1$（-{zh-tw:行; zh-cn:列;}-向量）
$V$	$={𝐱}^T(n)$ 是 $1\times (p+1)$（-{zh-tw:列; zh-cn:行;}-向量）
$C$	$={𝐈}_1$ 是 $1\times 1$ 單位矩陣

依照伍德伯里矩陣恆等式，可得到下式

${𝐑}_x^{-1}(n)$	$=$	${[\lambda {𝐑}_x(n-1)+𝐱(n){𝐱}^T(n)]}^{-1}$
	$=$	$\frac{1}{\lambda }\{{𝐑}_x^{-1}(n-1)-\frac{{𝐑}_x^{-1}(n-1)𝐱(n){𝐱}^T(n){𝐑}_x^{-1}(n-1)}{\lambda +{𝐱}^T(n){𝐑}_x^{-1}(n-1)𝐱(n)}\}$
		${\displaystyle }$

為了和標準的文獻一致，定義

$𝐏(n)$	$={𝐑}_x^{-1}(n)$
	$={\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)$

其中的增益向量$g(n)$為

$𝐠(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n){\{1+{𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)\}}^{-1}$
	$=𝐏(n-1)𝐱(n){\{\lambda +{𝐱}^T(n)𝐏(n-1)𝐱(n)\}}^{-1}$

在往下推導之前，需要將$𝐠(n)$改為以下的形式

$𝐠(n)\{1+{𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)\}$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)$
$𝐠(n)+𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)$

等式兩側減去左邊的第二項，得到

$𝐠(n)$	$={\lambda }^{-1}𝐏(n-1)𝐱(n)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)𝐱(n)$
	$={\lambda }^{-1}[𝐏(n-1)-𝐠(n){𝐱}^T(n)𝐏(n-1)]𝐱(n)$

配合$𝐏(n)$的遞迴式定義，希望的形式如下

$𝐠(n)=𝐏(n)𝐱(n)$

此時就可以完成遞迴，如以上討論

${𝐰}_n$	$=𝐏(n){𝐫}_{dx}(n)$
	$=\lambda 𝐏(n){𝐫}_{dx}(n-1)+d(n)𝐏(n)𝐱(n)$

第二步是從${𝐫}_{dx}(n)$的遞迴式定義開始，接著使用$𝐏(n)$的遞迴式定義，配合調整後的$𝐠(n)$，可以得到

${𝐰}_n$	$=\lambda [{\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)]{𝐫}_{dx}(n-1)+d(n)𝐠(n)$
	$=𝐏(n-1){𝐫}_{dx}(n-1)-𝐠(n){𝐱}^T(n)𝐏(n-1){𝐫}_{dx}(n-1)+d(n)𝐠(n)$
	$=𝐏(n-1){𝐫}_{dx}(n-1)+𝐠(n)[d(n)-{𝐱}^T(n)𝐏(n-1){𝐫}_{dx}(n-1)]$

配合${𝐰}_{n-1}=𝐏(n-1){𝐫}_{dx}(n-1)$，可以得到以下的更新方程式

${𝐰}_n$	$={𝐰}_{n-1}+𝐠(n)[d(n)-{𝐱}^T(n){𝐰}_{n-1}]$
	$={𝐰}_{n-1}+𝐠(n)\alpha (n)$

其中$\alpha (n)=d(n)-{𝐱}^T(n){𝐰}_{n-1}$ 是先驗誤差。將此和後驗誤差（在濾波器更新後計算的誤差）比較

$e(n)=d(n)-{𝐱}^T(n){𝐰}_n$

這就找到了修正因子

$\mathrm{\Delta }{𝐰}_{n-1}=𝐠(n)\alpha (n)$

這個結論指出了修正係數直接和誤差和增益向量成正比，增益向量會透過加權因子$\lambda$影響想要的靈敏度，這個結論很符合直覺。

RLS演算法摘要

p階RLS濾波器的演算法可以摘要如下

參數：	$p=$階數
	$\lambda =$遺忘因子
	$\delta =𝐏(0)$的初始值
開始：	$𝐰(0)=0$,
	$x(k)=0,k=-p,\dots ,-1$,
	$d(k)=0,k=-p,\dots ,-1$
	$𝐏(0)=\delta I$其中$I$是$p+1$階的單位矩陣
計算：	針對$n=1,2,\dots$
	$𝐱(n)=\left[\begin{array}{c}x(n)\\ x(n-1)\\ ⋮\\ x(n-p)\end{array}\right]$
	$\alpha (n)=d(n)-{𝐱}^T(n)𝐰(n-1)$
	$𝐠(n)=𝐏(n-1)𝐱(n){\{\lambda +{𝐱}^T(n)𝐏(n-1)𝐱(n)\}}^{-1}$
	$𝐏(n)={\lambda }^{-1}𝐏(n-1)-𝐠(n){𝐱}^T(n){\lambda }^{-1}𝐏(n-1)$
	$𝐰(n)=𝐰(n-1)+\alpha (n)𝐠(n)$.

$P$的遞迴依照代數Riccati方程，也類似卡尔曼滤波的結果。

相關條目

• 自适应滤波器
• Template:Link-en
• 最小均方滤波器
• Template:Link-en

書目

• Template:Cite book
• Simon Haykin, Adaptive Filter Theory, Prentice Hall, 2002, Template:ISBN
• M.H.A Davis, R.B. Vinter, Stochastic Modelling and Control, Springer, 1985, Template:ISBN
• Weifeng Liu, Jose Principe and Simon Haykin, Kernel Adaptive Filtering: A Comprehensive Introduction, John Wiley, 2010, Template:ISBN
• R.L.Plackett, Some Theorems in Least Squares, Biometrika, 1950, 37, 149–157, Template:ISSN
• C.F.Gauss, Theoria combinationis observationum erroribus minimis obnoxiae, 1821, Werke, 4. Gottinge