蚌线

绿色为直线，黑色为直线外一点，所有红色线段和蓝色线段的长度均相等。紫色和橙色曲线是绿色直线关于黑色点的蚌线，紫色为内支，橙色为外支

极点和原直线不变、迹距不同的一系列蚌线

在平面几何中，蚌线是一类曲线，可以由一条给定的曲线、一个定点和一个给定的长度来确定。更具体地说，过定点 $O$ 的动直线与给定曲线 $c$ 相交，动直线上满足“与交点距离为定长 $k$ ”的点的轨迹定出的新曲线，就是原曲线 $c$ 关于极点 $O$ 和迹距 $k$ 的蚌线。

用解析几何的方式来表述：平面曲线 $c$ 的极坐标方程为 $\rho =f(\theta )$ ，则以 $\rho =f(\theta )\pm k$ 为方程的曲线是 $c$ 关于原点的蚌线。

“蚌线”也常特指原曲线为直线的蚌线，即尼科美迪斯蚌线。Template:Tsl是古希腊数学家，他利用这种蚌线来解决古希腊数学三大难题中的两个——三等分角和倍立方体。

尼科美迪斯蚌线

灰色为直线，黑色为蚌线的极点
Template:Legend-line Template:Legend-line Template:Legend-line

性质

有定直线 $l$ 和直线外一固定点 $O$，过点 $O$ 的动直线与 $l$ 相交，动直线上满足“与交点距离为定长”的点的轨迹，就是直线 $l$ 关于极点 $O$ 的蚌线 $c$ ，即尼科美迪斯蚌线。一条尼科美迪斯蚌线有内外两支，两支的渐近线都为 $l$ 。

通常记 $l$ 与点 $O$ 的距离为 $a$ ，迹距为 $b$。根据 $a$ 和 $b$ 的关系，内支有三种不同形态：

• 当 $b<a$ 时，蚌线内支没有尖点或结点，极点与内支不相交。
• 当 $a=b$ 时，蚌线内支有一个尖点，尖点与极点重合。
• 当 $b>a$ 时，蚌线内支有一个结点，结点与极点重合。

尼科美迪斯蚌线是轴对称图形，对称轴与 $l$ 垂直并通过极点 $O$。

历史和应用

尼科米迪斯发明的工具，用来绘制直线蚌线的外支

古希腊数学家Template:Tsl是最早研究蚌线的人。他发明了绘制直线之蚌线的工具，这是人们第一次用仪器绘制出直线和圆之外的几何曲线。他关于蚌线的论著已经失传，只有一部分通过帕普斯的《数学汇编》得以保存下来。帕普斯指出，存在“四种”蚌线，但只记录了“第一种”蚌线，也就是直线蚌线的外支，用来解决尺规作图三大难题中的两个：三等分角和倍立方体。剩下的“三种”蚌线，很可能指的是直线蚌线内支的三种形态。

帕普斯将该曲线称为“螺线”（Template:Lang），这很可能是尼科美迪斯最初的叫法。后来的普罗克洛等人才改称该曲线为“蚌线”（Template:Lang）。

17世纪的大数学家艾萨克·牛顿认为蚌线是仅次于直线和圆的、定义第三简洁的曲线，并利用蚌线构造出多种三次平面曲线。但及至当代，蚌线变得很少被数学家研究和关注。

倍立方体

借助蚌线作出长度为$\sqrt[3]{2}$的线段

作线段 $AB=1$ 。以点 $A$ 为圆心、$AB$ 为半径作圆，以点 $B$ 为圆心、$AB$ 为半径作圆，交于点 $C$ 。

过点 $A$ 作线段 $AC$ 的垂线 $l$。以点 $C$ 为极点、$AB$ 为迹距作直线 $l$ 的蚌线外支。

延长 $BA$ 交蚌线于点 $D$ 。延长 $AB$ 交圆 $B$ 于点 $E$ 。连接 $CD$ 交 $l$ 于点 $F$ 。线段 $CF$ 的长度即为 $\sqrt[3]{2}$ 。

代数证明
设 $CF=x$ 。显然 $x$ 是正实数。 因为 $\mathrm{△}AFC$ 为直角三角形，所以 $AF=\sqrt{C{F}^2-C{A}^2}=\sqrt{x^2-1}$ 。 又因为 $\mathrm{△}ADF\sim \mathrm{△}EDC$ ，所以 $AF=\frac{EC}{CD}\cdot FD=\frac{\sqrt{3}}{x+1}$ 。 $\sqrt{x^2-1}=\frac{\sqrt{3}}{x+1}$ $(x^2-1)(x+1{)}^2=3$ $x^4+2x^3-2x-4=0$ $(x+2)(x^3-2)=0$ $x^3-2=0$ $x=\sqrt[3]{2}$

尼科美迪斯的几何证明
作长方形 $ABGH$ ，$AH=BG=2AB=2GH$ 。 延长 $DH$ ，延长 $BG$ ，交于点 $K$ 。 连接 $EH$ ，交 $BG$ 于点 $L$ ，点 $L$ 是 $BG$ 中点。 取 $AB$ 中点 $M$，连接 $MC$ 。
$AD\cdot BD=(MD-MA)\cdot (MD+MB)$ $AD\cdot BD+M{A}^2=M{D}^2$ $AD\cdot BD+M{A}^2+M{C}^2=M{D}^2+M{C}^2$ $AD\cdot BD+A{C}^2=C{D}^2$
$\mathrm{△}KBD\sim \mathrm{△}KGH\sim \mathrm{△}HAD$ $KG:GH=HA:AD$ $\because GH=GL,AH=2AB=AE$ $\therefore KG:GL=AE:AD=FC:FD$ $\because FD=AB=GL$ $\therefore KG=FC$ $KL=KG+GL=FC+FD=CD$ $K{L}^2=C{D}^2$
$K{L}^2=(KL+GL)\cdot (KL-GL)+G{L}^2$ $K{L}^2=KB\cdot KG+G{L}^2$ $C{D}^2=AD\cdot BD+A{C}^2$ $\therefore KB\cdot KG+G{L}^2=AD\cdot BD+A{C}^2$ $KB\cdot KG=AD\cdot BD$ $AD:KG=KB:BD=KG:GH=HA:AD$
$HA:AD=AD:KG=KG:GH$ $HA=2GH$ $\therefore KG=\sqrt[3]{2}GH$

三等分角

借助蚌线三等分任意锐角

作任意直角三角形 $\mathrm{△}OAB$ ，点 $A$ 为垂足。以点 $O$ 为极点、$2OB$ 为迹距作直线 $AB$ 的蚌线外支。

过点 $B$ 作直线 $AB$ 的垂线，交蚌线于点 $C$。 $OC$ 就是 $\mathrm{\angle }AOB$ 的三等分线。

证明
作 $OC$ 与 $AB$ 的交点 $D$ 。取 $CD$ 的中点 $E$ ，连接 $BE$ 。 根据蚌线和直角三角形的性质，可知 $OB=CE=DE=BE$ 。 易证得 $\mathrm{\angle }BOD=\mathrm{\angle }BED=\mathrm{\angle }EBC+\mathrm{\angle }C=2\mathrm{\angle }C=2\mathrm{\angle }AOD$ 。 故 $\mathrm{\angle }AOD=\frac{1}{3}\mathrm{\angle }AOB$ 。

解析几何

在极坐标系中，设点 $O$ 为坐标原点，则直线 $l$ 和蚌线 $c$ 的方程可以表示为：

$l:\rho =a\sec \theta$

$c:\rho =a\sec \theta \pm b$

$(-\frac{\pi }{2}<\theta <\frac{\pi }{2},a,b\in {ℝ}^{+})$

在直角坐标系中，设点 $O$ 为坐标原点，则直线 $l$ 和蚌线 $c$ 的方程可以表示为：

$l:x=a$

$c:(x-a{)}^2(x^2+y^2)=b^2{x}^2$

$(a,b\in {ℝ}^{+})$

或用参数方程表示为：

$\{\begin{array}{c}x=a\pm b\cos \theta \\ y=a\tan \theta \pm b\sin \theta \end{array}$

（上下正负号同号，$-\frac{\pi }{2}<\theta <\frac{\pi }{2},a,b\in {ℝ}^{+}$）

尼科美迪斯蚌线是四次平面曲线。

帕斯卡蜗线

Template:Main 帕斯卡蜗线是一类外旋轮线，同时也是一类特殊的蚌线，是圆关于圆上一个定点的蚌线。由于极点在原曲线上，所以蚌线的内支和外支光滑相连为一条曲线。当迹距等于圆的直径时，就是心脏线。

作圆 $O$ 关于圆上一个定点 $A$ 、迹距等于圆的半径的蚌线。对于圆上任意一点 $B$，延长 $BO$ 至圆外，与所作蚌线交于点 $C$。根据蚌线的性质，易知 $\mathrm{\angle }ACB=\frac{1}{3}\mathrm{\angle }AOB$ 。这条特殊的蚌线被称为Template:Le。

• 
  圆关于圆上一点、迹距小于圆径的蚌线
• 
  圆关于圆上一点、迹距等于圆径的蚌线，即心脏线
• 
  三等分角蜗线

其他蚌线

• 
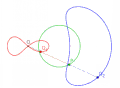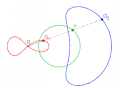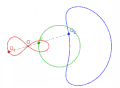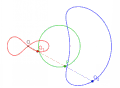
  圆对圆外一点的蚌线，迹距大于极点与圆的最大距离。极点与蚌线内支分离
• 
  圆对圆外一点的蚌线，迹距等于极点与圆的最大距离。极点为蚌线内支的尖点
• 
  圆对圆外一点的蚌线，迹距小于极点与圆的最大距离，大于极点与圆的最小距离。极点为蚌线内支的结点
• 
  圆对圆外一点的蚌线，迹距等于极点与圆的最小距离。极点为蚌线内支的尖点
• 
  圆对圆外一点的蚌线，迹距小于极点与圆的最小距离。极点与蚌线内支分离

• 
  圆对圆内一点的一条蚌线
• 
  抛物线对线外一点的一条蚌线
• 
  正弦曲线对线外一点的一条蚌线
• 
  立方曲线对线外一点的一条蚌线
• 
  双曲线一支对线上一点的蚌线
• 
  椭圆对于中心、迹距等于半短轴的蚌线，内支有两个重合的尖点