維格納分佈

維格納分布(又名韋格納分佈，英文: Wigner Distribution Function,縮寫為WDF) 是由1963年的諾貝爾物理學獎得主尤金·维格纳，于1932年首次引用的一個新的方程式。

眾所皆知，傅立葉變換對於研究穩態(時間獨立)的訊號(波形)是一項非常有用的工具，然而，訊號(波形)一般來說在時間上並非是獨立的，這樣的訊號或是波形傅立葉變換並無法有效地完全分析其特性，因此對於一個非穩態的訊號完全分析需要測量出時間以及頻率上的表現。本頁面介紹的數學函數是時頻分析中的基礎方法，在1980年，Claasen，Mecklenbrauker對WDF做了更進一步的研究。除此之外，線性時頻分析中，STFT、Gabor transform和WDF扮演了相當重要的角色，其中WDF對於分析很多非穩態的隨機訊號都有很好的表現，例如：量子力學、光學、聲學、通訊、生物工程、訊號處理和影像處理。有時也被用在分析地震的資料，以及處理聲音的相位失真。

定義

維格納分布有許多不同的定義，而此處的定義是特別針對時頻分析而定的。若給定一時間序列$x[t]$，它的非平穩自相關函數如下公式所列

　　　$C_x(t_1,t_2)=⟨(x[t_1]-\mu [t_1]){(x[t_2]-\mu [t_2])}^{*}⟩,$

其中$⟨\cdots ⟩$代表所有可能實驗的程序的平均，$\mu [t]$代表平均，其可能是時間的函數也有可能不是。維格納函數$W_x(t,f)$起初是以包含時間平均$t=(t_1+t_2)/2$與時間差$\tau =t_1-t_2$的自相關函數和時間差進行傅立葉轉換來表示，如下：

　　$W_x(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{C}_x(t+\frac{\tau }{2},t-\frac{\tau }{2})e^{-2\pi i\tau f}d\tau .$

對於單一零平均的時間序列，維格納函數可以簡化如下：

定義一

$W_x(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\frac{\tau }{2})x^{*}(t-\frac{\tau }{2})e^{-j2\pi \tau f}d\tau$.....(1)

定義二

$W_x(t,\omega )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\frac{\tau }{2})x^{*}(t-\frac{\tau }{2})e^{-j\omega \tau }d\tau$.....(2)

定義二與定義一之間的關係 : $\omega =2\pi f$

其他定義

$\sqrt{\frac{1}{2\pi }}{W}_x(t,\omega )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\frac{\tau }{2})x^{*}(t-\frac{\tau }{2})e^{-j\omega \tau }d\tau$.....(3)

在聲納和雷達系統中，傳送出去的聲波的反射波可以用來偵測目標物的位置跟速度，在很多情形下，收到的訊號因為都普勒位移，所以跟原本的訊號並不一樣。Woodward(1953) 改寫了原本的公式

$A_x(t,\omega )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\tau +\frac{t}{2})x^{*}(\tau -\frac{t}{2})e^{-j\omega \tau }d\tau$

這個公式被稱為Woodward ambiguity function，這個式子在雷達系統的訊號處理和設計上扮演重要的角色。

而維格納分布亦為科恩系列分布的其中一種特例，當科恩系列分布中的$\mathrm{\Phi }(\eta ,\tau )=1$時，科恩系列分布會是維格納分布。

WDF、STFT和Gabor的比較

WDF、STFT和Gabor都佔了時頻分析中非常重要的地位，在這邊比較一下WDF、STFT、Gabor和WDF的變體Cohen's Class Distribution之間的差別。

	WDF	STFT	Gabor	Cohen
清晰度	較好	較差	適中	偏差
相交項的問題	嚴重	無	輕微	嚴重
複雜度	高	低	中	高
處理隨機程序	可	不可	可	可
頻率分辨率	高	中	高	高
時間分辨率	高	中	中	高
能量集中性	較好	較差	適中	適中
數值穩定性	較差	較好	較好	較差

清晰度：描述時頻圖在時間和頻率域上解析信號細節的能力。

相交項的問題：多分量信號時可能出現不想要的相交項(cross term)，導致時頻圖難以解讀。

複雜度：指運算複雜度，較高的複雜度意味著需要更多的計算資源。

處理隨機程序：對具有隨機性質的信號進行有效分析和表徵的能力。

頻率分辨率：頻域解析度的能力，越高越能分辨接近的頻率分量。

時間分辨率：時間域解析度的能力，越高越能定位信號的時間變化。

能量集中性：時頻圖中能量分布是否聚集在主要分量，分散則會影響分析效果。

數值穩定性：算法在不同條件下（如隨機噪聲或非穩態信號）保持穩定表現的能力。

WDF的優缺點

在這裡列出WDF主要的優缺點

優點 :

1.有良好的解析度，尤其是對單一成分，且瞬時頻率變化不為2次式以上，適合分析瞬態與多變信號。

2.有良好的數學運算性質(見WDF的數學性質)。

3.對隨機過程和非穩態信號表現良好，可用於分析隨機程序(見WDF與隨機程序的關係)。

4.信號能量分佈高度集中於真實分量，便於解析信號結構。

5.在時間和頻率域上的邊際分佈與原始信號一致, 滿足投影性質。

6.提供準確的能量分佈估計，便於信號重建。

7.能準確表示信號瞬時頻率，有助於動態信號分析，有限制(缺點4)。

8.無窗函數限制，能解析接近頻率分量。

9.對非線性信號具有優勢，便於非線性行為檢測。

10.對含有噪聲或隨機成分的信號也能表現出色。

缺點 :

1.有相交項(cross term)的問題，降低時頻圖可解讀性，改進方法請見 改進型韋格納分佈。

2.需執行二維積分或卷積，對計算資源要求高。若訊號時間越長，則需要更久的時間。

3.不是一對一函數，無法辨別相位部分，例如: $WDF[x(t)]=WDF[x(t)e^{j\varphi }]$

4.不適合分析瞬時頻率變化為2次式以上的型態，即$e^{j{t}^n},n\ne 0,1,2$。

5.低信噪比環境下，噪聲可能被放大，影響準確性。

6.不滿足線性運算，影響某些應用的便利性。

7.結果分佈可能對輸入條件敏感，缺乏唯一性。

相交項特性

WDF不是一個線性的轉換，由於$x(t)$的signal auto-correlation function $x(t+\frac{\tau }{2})x^{*}(t-\frac{\tau }{2})$，如果有兩種以上不同性質的訊號疊加，會產生相交項。然而相交項卻有重要且有用的物理意義，像是可以用來分析期望值，相反的，短時距傅立葉轉換就沒有此特性，詳見維格納分佈與隨機程序的關係。以下數學方程式對於WDF後會產生相交項。

• $x(t)=\{\begin{array}{cc}\cos (2\pi t)& t\le -2\\ \cos (4\pi t)& -2<t\le 2\\ \cos (3\pi t)& t>2\end{array}$

• $x(t)=e^{i{t}^3}$

WDF與隨機程序的關係

對於一個隨機程序x(t)，我們無法得知其確切的值，因此會將其值表示為一個機率函數，通常E[x(t)] = 0 for any t

將x(t)的維格納分布取期望值後可得其譜密度(Power spectral density，PSD)，如下公式所列

$E[W_x(t,f)]=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}E[x(t+\tau /2)x^{*}(t-\tau /2)]\cdot e^{-j2\pi f\tau }\cdot d\tau$

$=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{R}_x(t,\tau )\cdot e^{-j2\pi f\tau }\cdot d\tau =S_x(t,f)$

當x(t)的統計特性不隨時間變化時，可稱x(t)為平穩的隨機程序，其譜密度也可簡化為$E[W_x(t,f)]=S_x(f)$，也就是說維格納函數能初略的告訴我們譜密度如何隨時間進行變化。維格納函數能在平穩程序對所有時間ｔ都簡化成譜密度，然而也等同於非平穩的自相關函數，這也是維格納分布的動機。

下圖為一個平穩的隨機程序進行維格納分析後的例子，可明顯看出此信號不隨時間變化，也就是時頻分析結果為水平線。反之，亦可利用時頻分析結果是否為水平線判斷該訊號是否為一平穩的訊號。

而在訊號處理中常見的白雜訊，其譜密度$S_x(f)=\sigma$，其中$\sigma$為一個常數。白雜訊的維格納分布如下圖，可看出此雜訊在所有時間及頻率都存在著。

維格納分布的相交項在處理隨機程序時派上用場，相對的，沒有相交項的短時距傅立葉轉換，則無法用於隨機程序，如下公式所示，只有在零平均隨機程序時，$E[X(t,f)]=0$

$E[X(t,f)]=E[\underset{t-B}{\overset{t+B}{\int }}x(\tau )w(t-\tau )e^{-j2\pi f\tau }d\tau ]=\underset{t-B}{\overset{t+B}{\int }}E[x(\tau )]w(t-\tau )e^{-j2\pi f\tau }d\tau$

常見的時頻分析例子

以下的例子說明如何用WDF來做時頻分析

常數訊號

輸入訊號為常數，則時頻分佈為一條線重合於時軸，如果'x(t) = 1，則：

$W_x(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{-i2\pi \tau f}d\tau =\delta (f).$

弦波訊號

輸入訊號為弦波，則時頻分佈為一條線平行於時軸，如果Template:Math，則：

$\begin{array}{cc}{W}_x(t,f)& =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{i2\pi k(t+\frac{\tau }{2})}{e}^{-i2\pi k(t-\frac{\tau }{2})}{e}^{-i2\pi \tau f}d\tau \\ & =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{-i2\pi \tau (f-k)}d\tau \\ & =\delta (f-k).\end{array}$

啁啾聲信號

啁啾聲訊號的瞬時頻率隨時間線性，表示時頻分佈為一條斜值線，例如

$x(t)=e^{i2\pi k{t}^2}$ ,

則瞬時頻率為：

$\frac{1}{2\pi }\frac{d(2\pi k{t}^2)}{dt}=2kt,$

故WDF為：

$\begin{array}{cc}{W}_x(t,f)& =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{i2\pi k{(t+\frac{\tau }{2})}^2}{e}^{-i2\pi k{(t-\frac{\tau }{2})}^2}{e}^{-i2\pi \tau f}d\tau \\ & =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{i4\pi kt\tau }{e}^{-i2\pi \tau f}d\tau \\ & =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{-i2\pi \tau (f-2kt)}d\tau \\ & =\delta (f-2kt).\end{array}$

余弦訊號

x(t) = cos(440$\pi$t), 当 t 小於 0.5， 頻率 f = 220Hz
x(t) = cos(660$\pi$t), 当 0.5 小於等於 t 小於 1， 頻率 f = 330Hz
x(t) = cos(524$\pi$t), 当 t 大於等於 1， 頻率 f = 262Hz

單位脈衝訊號

因為單位脈衝包含所有的頻率分佈，且在時間不等於零時沒值，故WDF為通過原點的且與時軸垂直的線

$\begin{array}{cc}{W}_x(t,f)& =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\delta (t+\frac{\tau }{2})\delta (t-\frac{\tau }{2})e^{-i2\pi \tau f}d\tau \\ & =4\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\delta (2t+\tau )\delta (2t-\tau )e^{-i2\pi \tau f}d\tau \\ & =4\delta (4t)e^{i4\pi tf}\\ & =\delta (t)e^{i4\pi tf}\\ & =\delta (t).\end{array}$

方波訊號

$x(t)=\{\begin{array}{cc}1& |t|<1/2\\ 0& \text{otherwise}\end{array}$ ,

$W_x(t,f)=\frac{1}{\pi f}\sin (f[1-2|t|])$ .

WDF的數學性質

(1)投射特性	$|x(t){|}^2=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(t,f)df$, $|X(f){|}^2=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(t,f)dt$
(2)能量特性	$|x(t){|}^2=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\iint }}{W}_x(t,f)dtdf=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|x(t){|}^{2}dt=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|X(f){|}^{2}df$
(3)回覆特性	$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(\frac{t}{2},f)e^{j2\pi ft}df=x(t)\bullet x^{*}(0)$, $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(t,\frac{f}{2})e^{-j2\pi ft}dt=X(f)\bullet X^{*}(0)$
(4)Mean 條件	If $x(t)=|x(t)|e^{j2\pi \varphi (t)},X(f)=|X(f)|e^{j2\pi \mathrm{\Psi }(f)}$ then ${\varphi }^{\prime }(t)={|x(t)|}^{-2}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f\times W_x(t,f)df$, $-{\mathrm{\Psi }}^{\prime }(f)={|X(f)|}^{-2}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}t\times W_x(t,f)dt$
(5)Moment特性	$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\iint }}{t}^n{W}_x(t,f)dtdf=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{t}^n|x(t){|}^{2}dt$, $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\iint }}{f}^n{W}_x(t,f)dtdf=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{f}^n|X(f){|}^{2}dt$
(6)$W_x(t,f)$是實數	$\overline{W_x(t,f)}=W_x(t,f)$
(7)區域特性	If $x(t)=0$ for $t>t_0$ then $W_x(t,f)=0$ for $t>t_0$, If $x(t)=0$ for $t<t_0$ then $W_x(t,f)=0$ for $t<t_0$
(8)乘法特性	If $y(t)=x(t)h(t)$,then $W_y(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(t,\rho )W_h(t-\rho ,f)d\rho$
(9)摺積特性	If $y(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t-\tau )h(\tau )d\tau$,then $W_y(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(\rho ,f)W_h(t-\rho ,f)d\rho$
(10)相關特性	If $y(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\tau )h^{*}(\tau )d\tau$,then $W_y(t,\omega )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{W}_x(\rho ,\omega )W_h(-t+\rho ,\omega )d\rho$
(11)時間平移特性	If $y(t)=x(t-t_0)$, then $W_y(t,f)=W_x(t-t_0,f)$
(12)調變特性	If $y(t)=e^{j2\pi f_{0}t}x(t)$, then $W_y(t,f)=W_x(t,f-f_0)$

WDF的數學性質證明

WDF滿足永遠是實數的性質，以下是證明:

$W_x(t,f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\frac{\tau }{2})x^{*}(t-\frac{\tau }{2})e^{-j2\pi f\tau }d\tau$

$\overline{W_x(t,f)}=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^{*}(t+\frac{\tau }{2})x(t-\frac{\tau }{2})e^{j2\pi f\tau }d\tau$

令 ${\tau }^{\prime }=-\tau$代入，變數乘上負號，因此積分範圍會變成$\mathrm{\infty }$到$-\mathrm{\infty }$

$\begin{array}{cc}\overline{W_x(t,f)}& =\underset{\mathrm{\infty }}{\overset{-\mathrm{\infty }}{\int }}{x}^{*}(t-\frac{{\tau }^{\prime }}{2})x(t+\frac{{\tau }^{\prime }}{2})e^{-j2\pi f{\tau }^{\prime }}(-d{\tau }^{\prime })\\ & =-\underset{\mathrm{\infty }}{\overset{-\mathrm{\infty }}{\int }}{x}^{*}(t-\frac{{\tau }^{\prime }}{2})x(t+\frac{{\tau }^{\prime }}{2})e^{-j2\pi f{\tau }^{\prime }}d{\tau }^{\prime }\\ & =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(t+\frac{{\tau }^{\prime }}{2})x^{*}(t-\frac{{\tau }^{\prime }}{2})e^{-j2\pi f{\tau }^{\prime }}\\ & =W_x(t,f)\end{array}$

故WDF永遠是實數

WDF實現方法

以下為電腦計算WDF的實現方式

1. 直接運算(暴力法) 複雜度：$TF(2Q+1)$
2. 使用離散傅立葉變換 複雜度：$TN{\log }_{2}N$
3. 使用Chirp-Z 轉換 複雜度 : $TN{\log }_{2}N$，通常為使用離散傅立葉變換的2~3倍，但限制比使用離散傅立葉變換少

在使用這三個方法前，先來做個前提討論

從定義一出發

$W_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau$

令 ${\tau }^{\prime }=\tau /2$

$W_x\left(t,f\right)=2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x\left(t+{\tau }^{\prime }\right)\cdot x^{*}\left(t-{\tau }^{\prime }\right)e^{-j4\pi {\tau }^{\prime }f}\cdot d{\tau }^{\prime }$

再令 $t=n{\mathrm{\Delta }}_t,f=m{\mathrm{\Delta }}_f,{\tau }^{\prime }=p{\mathrm{\Delta }}_t$ ，則上述式子則為

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2\sum _{p=-\mathrm{\infty }}^{\mathrm{\infty }}x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)\exp \left(-j4\pi mp{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f\right){\mathrm{\Delta }}_t$

下面介紹的三種方法都是從這條式子開始推導

注意事項 :

若x(t)是無限長的訊號，則p要從負無限加到正無限，這點不易實現。

若x(t)為有限長的訊號，則p範圍可以縮小，就可能實現。

故下面三種方法都是在第2種情況下討論，即x(t)為有限長訊號，p範圍可以縮小

我們假設$x(t)=0fort<n_1{\mathrm{\Delta }}_{t}andt>n_2{\mathrm{\Delta }}_t$

直接運算(暴力法)

限制條件 :

只有一個 : 要滿足Nyquist criterion

${\mathrm{\Delta }}_t<\frac{1}{2B}$，其中B是$x\left(t+\tau \right)x^{*}\left(t-\tau \right)$的頻寬，大約是x(t)的兩倍。

推導 :

$x(t)=0fort<n_1{\mathrm{\Delta }}_{t}andt>n_2{\mathrm{\Delta }}_t$

所以當$n+p\notin [n_1,n_2]\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{-}\mathrm{p}\notin \mathrm{[}{n}_1,n_2\mathrm{]}$ 時，

$x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)=0$

固定中間的n值 ($n{\mathrm{\Delta }}_t$) 來探討p的範圍

$n_1\le n+p\le n_2\to n_1-n\le p\le n_2-n$

即 $\max (n_1-n,n-n_2)\le p\le \min (n_2-n,n-n_1)$-– (1)

$n_1\le n-p\le n_2\to {\mathrm{n}}_1-n\le -p\le n_2-n\to n-n_2\le p\le n-n_1$

即 $-\min (n_2-n,n-n_1)\le p\le \min (n_2-n,n-n_1)$-- (2)

其中 (1) & (2) 的下限是同義的

故(1) & (2)皆可改寫為

$-\min (n_2-n,n-n_1)\le p\le \min (n_2-n,n-n_1)$

且可以發現 $(n_2-n){\mathrm{\Delta }}_t,(n-n_1){\mathrm{\Delta }}_t$ 代表 $n{\mathrm{\Delta }}_t$ 離兩個邊界的距離

注意事項： 當 n > n2 或 n < n1 時，將沒有 p 能滿足上面的不等式

最後推導出的式子如下

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2\sum _{p=-Q}^{Q}x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)\exp \left(-j4\pi mp{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f\right){\mathrm{\Delta }}_t$

其中 $Q=\min (n_2-n,n-n_1),p\in [-Q,Q],n\in [n_1,n_2]$

使用離散傅立葉變換

限制條件 :

(1)要滿足Nyquist criterion

${\mathrm{\Delta }}_t<\frac{1}{2B}$，其中B是$x\left(t+\tau \right)x^{*}\left(t-\tau \right)$的頻寬，大約是x(t)的兩倍。

(2)${\mathrm{\Delta }}_t{\mathrm{\Delta }}_f=\frac{1}{2N}$

(3) $N\ge 2Q+1$

推導 :

前提討論的式子可以改寫為

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2{\mathrm{\Delta }}_t\sum _{p=-Q}^{Q}x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)e^{-j\frac{2\pi mp}{N}}$

令$q=p+Q\to p=q-Q$

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2{\mathrm{\Delta }}_t{e}^{j\frac{2\pi mQ}{N}}\sum _{q=0}^{2Q}x\left((n+q-Q){\mathrm{\Delta }}_t\right)x^{*}\left((n-q+Q){\mathrm{\Delta }}_t\right)e^{-j\frac{2\pi mq}{N}}$

針對中間$x\left((n+q-Q){\mathrm{\Delta }}_t\right)x^{*}\left((n-q+Q){\mathrm{\Delta }}_t\right)$項

令

$c_1\left(q\right)=x\left((n+q-Q){\mathrm{\Delta }}_t\right)x^{*}\left((n-q+Q){\mathrm{\Delta }}_t\right),for\mathrm{0}\le q\le 2\mathrm{Q}$

$c_1\left(q\right)=0,for\mathrm{2}Q+1\le q\le N-1$

最後得出的式子如下

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2{\mathrm{\Delta }}_t{e}^{j\frac{2\pi mQ}{N}}\sum _{q=0}^{N-1}{c}_1\left(q\right)e^{-j\frac{2\pi mq}{N}}$

其中

$Q=\min (n_2-n,n-n_1),n\in [n_1,n_2]$

$c_1\left(q\right)=x\left((n+q-Q){\mathrm{\Delta }}_t\right)x^{*}\left((n-q+Q){\mathrm{\Delta }}_t\right),for\mathrm{0}\le q\le 2\mathrm{Q}$

$c_1\left(q\right)=0,for\mathrm{2}Q+1\le q\le N-1$

使用Chirp-Z 轉換

限制條件 :

只有一個 : 要滿足Nyquist criterion

${\mathrm{\Delta }}_t<\frac{1}{2B}$，其中B是$x\left(t+\tau \right)x^{*}\left(t-\tau \right)$的頻寬，大約是x(t)的兩倍。

推導 :

前提討論的式子可改寫為

$W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2{\mathrm{\Delta }}_t{e}^{-j2\pi m^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}\sum _{p=-Q}^{Q}x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)e^{-j2\pi p^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}{e}^{j2\pi {(p-m)}^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}$

計算分成3步驟

STEP 1 : $x_1\left(n,p\right)=x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)e^{-j2\pi p^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}$

STEP 2 : $X_2\left[n,m\right]=\sum _{p=n-Q}^{n+Q}{x}_1\left[p\right]c\left[m-p\right]$ , 其中$c\left[m\right]=e^{j2\pi m^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}$

STEP 3 : $X\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2{\mathrm{\Delta }}_t{e}^{-j2\pi m^2{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}{X}_2\left[n,m\right]$

延伸變化

視窗型韋格納分佈

視窗型韋格納分佈（Template:Lang），在韋格納分佈中，當x(t)為無限長訊號時，WDF很難去實現它。所以在積分中加入一個新的函數 ，目的是擷取x(t)中的片段來計算，不需從負無限積分到正無限。

定義

$W_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w\left(\tau \right)x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau$ ， 其中$w(\tau )$為實數且為有限長訊號

原始韋格納分佈定義 $W_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau$

優缺點

• 優點 :

1. 降低運算時間，因為$w(\tau )$為有限長函數。
2. 可以有效降低相交項(cross term)問題，但不能完全消除(詳見下方說明)。

• 缺點 :

1. 一些相交項(cross term)問題仍被保留。
2. 可能不符合譜密度(Power spectral density)的定義。
3. 一些好用的數學運算性質會消失。

實現方法

從定義出發 $W_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w\left(\tau \right)x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau$ 令$\tau ={\tau }^{\prime }/2$ $W_x\left(t,f\right)=2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w\left(2{\tau }^{\prime }\right)x\left(t+{\tau }^{\prime }\right)\cdot x^{*}\left(t-{\tau }^{\prime }\right)e^{-j4\pi {\tau }^{\prime }f}\cdot d{\tau }^{\prime }$ 再令$t=n{\mathrm{\Delta }}_t,f=m{\mathrm{\Delta }}_f,{\tau }^{\prime }=p{\mathrm{\Delta }}_t$ $W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2\sum _{p=-\mathrm{\infty }}^{\mathrm{\infty }}w\left(2p{\mathrm{\Delta }}_t\right)x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)e^{-j4\pi mp{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}{\mathrm{\Delta }}_t$ 假設w(t) = 0 for |t| > B 即 $w\left(2p{\mathrm{\Delta }}_t\right)=0forp<-Q\wedge p>Q$ 其中$Q=\frac{B}{2{\mathrm{\Delta }}_t}$ 如此一來，p範圍便可縮小。 $W_x\left(n{\mathrm{\Delta }}_t,m{\mathrm{\Delta }}_f\right)=2\sum _{p=-Q}^{Q}w\left(2p\right)x\left((n+p){\mathrm{\Delta }}_t\right)x^{*}\left((n-p){\mathrm{\Delta }}_t\right)e^{-j4\pi mp{\mathrm{\Delta }}_t{\mathrm{\Delta }}_f}{\mathrm{\Delta }}_t$

避免相交項的原因

從定義出發 $W_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w\left(\tau \right)x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau$，其中$w(\tau )$為實數且為有限長訊號

假設$x(t)\mathrm{=}\delta (t-t_1)+\delta (t-t_2)$的情況下，比較有無mask function所產生的不同結果

x(t)示意圖

理想情形 : $W_x(t,f)\mathrm{=}\mathrm{0}fort\ne t_1,t_2$

沒有使用mask function

即mask function $w(\tau )=1$

$\begin{array}{c}{W}_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau \\ =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\left[\delta \left(t+\frac{\tau }{2}-t_1\right)+\delta \left(t+\frac{\tau }{2}-t_2\right)\right]\cdot \left[\delta \left(t-\frac{\tau }{2}-t_1\right)+\delta \left(t-\frac{\tau }{2}-t_2\right)\right]e^{-j2\pi \tau f}\cdot d\tau \\ =4\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{firstterm}{\underbrace{\left[\delta \left(\tau +2t-2t_1\right)+\delta \left(\tau +2t-2t_2\right)\right]}}\cdot \underset{secondterm}{\underbrace{\left[\delta \left(\tau -2t+2t_1\right)+\delta \left(\tau -2t+2t_2\right)\right]}}{e}^{-j2\pi \tau f}\cdot d\tau \end{array}$

Wx(t,f)示意圖

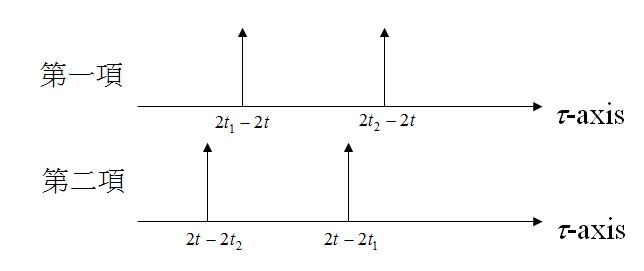
總共有3種情況要討論，如下圖，可見cross term在沒有使用mask function時，無法被消除

ideal x(t)。Auto term 為自相關項。 Cross term為相交項

使用mask function

$\begin{array}{c}{W}_x\left(t,f\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w(\tau )x\left(t+\tau /2\right)\cdot x^{*}\left(t-\tau /2\right)e^{-j2\pi \tau f}\cdot d\tau \\ =4\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}w(\tau )\underset{firstterm}{\underbrace{\left[\delta \left(\tau +2t-2t_1\right)+\delta \left(\tau +2t-2t_2\right)\right]}}\cdot \underset{secondterm}{\underbrace{\left[\delta \left(\tau -2t+2t_1\right)+\delta \left(\tau -2t+2t_2\right)\right]}}{e}^{-j2\pi \tau f}\cdot d\tau \end{array}$

假設$w(\tau )=0for|\tau |>B>0$，且$B<{\mathrm{t}}_2\mathrm{-}{\mathrm{t}}_1$

由於$w(\tau )$只在-B到B有值，故乘上$w(\tau )$就能去除相交項(Cross term)，只保留下圖中兩條紅線中間的區域，也就是Auto terms。

ideal x(t)。

但上述其實是理想的情況，x(t)為窄頻信號Delta function

如果X(τ)寬度太寬或是有ripple的話，Cross term仍會有殘留，示意圖如下

non ideal x(t)。

藍色線為X(τ)的訊號，若X(τ)的寬度太寬或是有ripple產生，就可能會跑進$w(\tau )$的範圍裡面，進而導致無法完全濾除Cross term。

總結

cross term 只有在訊號每個成分的寬度都小於2B，且時間差$t_2-t_1$都大於B時，才能被消除

改進型韋格納分佈

此方法可以消除相交項(cross term)。

加伯–韋格納轉換

消除相交項(cross term)問題，在某些情況下比加伯轉換擁有更好的清晰度。

参见

• 闵可夫斯基空间
• 柯西不等式
• 三角不等式
• 完备空间

參考書目、資料來源

• Jian-Jiun Ding, Time frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2018.
• Jian-Jiun Ding, Time-frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2021.
• Jian-Jiun Ding, Time-frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2023.
• Jian-Jiun Ding, Time-frequency analysis and wavelet transform class note, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2024.