小十二面截半二十面體

Template:NoteTA Template:Not Template:Infobox polyhedron 在幾何學中，小十二面截半二十面體是一種由正五邊形、正十邊形和正三角形組成的星形均勻多面體，外觀與小斜方截半二十面體十分相似Template:Rp，其索引為U₃₃，是Template:Link-wd的對偶多面體，具有Template:Link-en，可以視為小斜方截半二十面體的Template:Link-en多面體。在Template:En-link中，小十二面截半二十面體可以表示為Template:CDD，在威佐夫記號中可以表示為Template:Nowrap。

性質

小十二面截半二十面體是一種非凸均勻多面體，由44個面、120條邊和60個頂點組成。在其44個面中，有20個正三角形面、12個正五邊形面和12個正十邊形面。

尺寸

令小十二面截半二十面體邊長為單位長，則其外接球半徑為：

$R=\frac{\sqrt{11+4\sqrt{5}}}{2}$

二面角

小十二面截半二十面體有兩種二面角，分別為十邊形面和五邊形面的交角以及十邊形面和三角形面的交角。

其中，十邊形面和五邊形面的交角約為116.565度：

$\arccos \left(\frac{-\sqrt{5}}{5}\right)\approx 2.0344439357957\approx 116.565051177^{\circ }$

十邊形面和三角形面的交角約為37.377度：

$\arccos \left(\frac{\sqrt{15(5+2\sqrt{5})}}{15}\right)=\arccos \left(\sqrt{\frac{5+2\sqrt{5}}{15}}\right)\approx 0.6523581\approx 37.377368^{\circ }$

分類

由於小十二面截半二十面體的頂點圖為交叉梯形且具備點可遞的特性，同時，其存在自相交的面，因此小十二面截半二十面體是一種自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra）。自相交擬擬正多面體一共有12種，除了小雙三角十二面截半二十面體外，其餘由阿爾伯特·巴杜羅（Albert Badoureau）於1881年發現並描述。

自相交擬擬正多面體
（Self-Intersecting Quasi-Quasi-Regular Polyhedra）

小立方立方八面體	大立方截半立方體	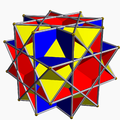非凸大斜方截半立方體	小十二面截半二十面體
大十二面截半二十面體	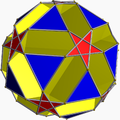小雙三角十二面截半二十面體	大雙三角十二面截半二十面體	Template:Link-wd
小二十面化截半二十面體	大二十面化截半二十面體	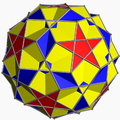斜方截半大十二面體	非凸大斜方截半二十面體

相關多面體

小十二面截半二十面體與小星形截角十二面體與均勻的Template:Link-en和Template:Link-en共用相同的頂點佈局。其亦與小斜方截半二十面体和小斜方十二面體共用相同的邊佈局。

小斜方截半二十面体	小十二面截半二十面體	小斜方十二面體
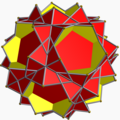小星形截角十二面體	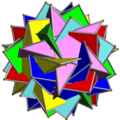Template:Link-en	Template:Link-en