小星形截角十二面體
Template:NoteTA Template:Not Template:Infobox polyhedron 在幾何學中,小星形截角十二面體是一種星形均勻多面體,由12個五邊形和12個十角星組成[1],並且與截角大十二面體拓樸同構[2],其對偶多面體為大五角化十二面體。[3]
性質
小星形截角十二面體是一種星形均勻多面體,共有24個面、90條邊和60個頂點[4],歐拉示性數為-6[5],並且具有二十面體群對稱性[6]。在小星形截角十二面體的60個頂點中每個頂點都是兩個十角星和一個五邊形的公共頂點,在頂點圖中,其可以用{10/3, 10/3, 5}來表示[7][8][5],由於每個頂點對應的角都是三面角、且等角,因此小星形截角十二面體也可以算是一種等角多面體[9]。
面的組成
小星形截角十二面體由24個面組成,在24個面中有12個面有5條邊組成、另外12個面由十條邊組成[10]。而這12個由十條邊組成的多邊性全部都是星形多邊形,即十角星[10]。
構成小星形截角十二面體的五邊形面 |
構成小星形截角十二面體的十角星面 |
 構成小星形截角十二面體的面在頂點周圍的排佈 |
二面角
小星形截角十二面體有兩種稜,一種是2個十角星的公共稜,其對應的二面角角度約為116.56度、另一種是十角星和五邊形的公共稜,其對應的二面角角度約為63.42度[11]。
小星形截角十二面體中,2個十角星的公共稜對應到的二面角角度為五分之負的五的平方根之反餘弦值[11],其等價於負的五的平方根的倒數之反餘弦值[2]:
小星形截角十二面體中,十角星和五邊形的公共稜對應到的二面角角度為五分之五的平方根之反餘弦值[11],其等價於正五的平方根的倒數之反餘弦值[2]:
歷史
最早列出小星形截角十二面體的文獻是在考克斯特、朗格·希金斯與米勒的論文《均勻多面體》中[12],其中列出了非常多的均勻多面體。後來在1993年時,齊夫·哈爾提出了一個能計算生成各均勻多面體的演算法,使得小星形截角十二面體能更容易地被視覺化。[5]
相關多面體
若將小星形截角十二面體視為一個抽象多面體,則其與截角大十二面體視為抽象多面體的結果等價[2]。另一種與小星形截角十二面體相關的多面體為皮特里擴展小星形截角十二面體,是由小星形截角十二面體經過皮特里擴展變換所形成的像,其共有114個面、300條邊和180個頂點。[13]
此外,小星形截角十二面體與截角大十二面體拓樸同構:小星形截角十二面體可以透過將五邊形面拓樸變形成五角星面同時也將十角星面拓樸變形成十邊形面使立體轉變成截角大十二面體。[14]
小星形截角十二面體與小斜方截半二十面体共用相同的頂點排佈。[2]其他也與小星形截角十二面體共用相同的頂點排佈的立體有小十二面截半二十面體[15]、小斜方十二面體[16]。
 小斜方截半二十面体 |
 小十二面截半二十面體 |
 小斜方十二面體 |
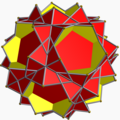 小星形截角十二面體 |
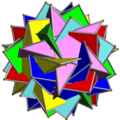 Template:Link-en |
 Template:Link-en |
參見
參考文獻
外部連結
Template:從星形正多面體變換的星形均勻多面體 Template:均勻多面體導航
- ↑ Template:Cite web
- ↑ 2.0 2.1 2.2 2.3 2.4 Template:Cite web
- ↑ Template:Cite mathworld
- ↑ 引用错误:
<ref>标签无效;未给name(名称)为Paul Bourke. 2004的ref(参考)提供文本 - ↑ 5.0 5.1 5.2 Template:Cite journal
- ↑ Template:Cite web
- ↑ 引用错误:
<ref>标签无效;未给name(名称)为Roman E. Maeder. 1995的ref(参考)提供文本 - ↑ Template:Cite web
- ↑ Template:Cite journal
- ↑ 10.0 10.1 Template:Cite web
- ↑ 11.0 11.1 11.2 Template:Cite web
- ↑ Template:Cite journal
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite web