包絡線

建立曲線族的包絡線。

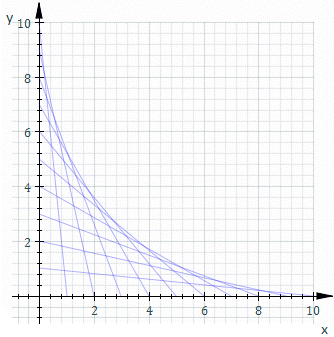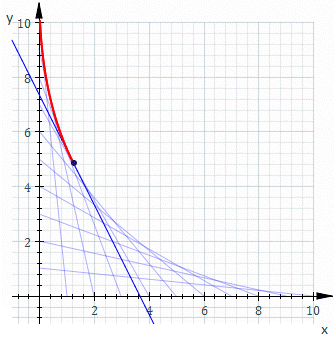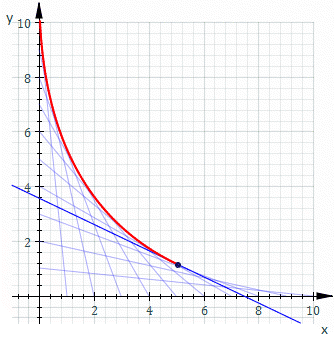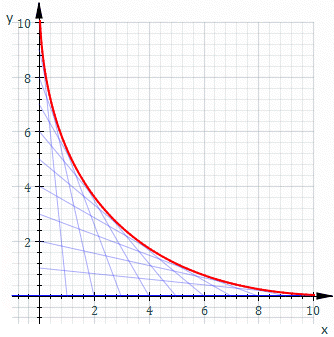
包絡線（Envelope）是幾何學裡的概念，代表一條曲線與某個曲線族中的每條線都有至少一點相切。（曲線族即一些曲線的無窮集，它們有一些特定的關係。）

設一個曲線族的每條曲線$C_s$可表示為$t\mapsto (x(s,t),y(s,t))$，其中$s$是曲線族的參數，$t$是特定曲線的參數。若包絡線存在，它是由$s\mapsto (x(s,h(s)),y(s,h(s)))$得出，其中$h(s)$以以下的方程求得：

$\frac{\partial y}{\partial h}\frac{\partial x}{\partial s}=\frac{\partial y}{\partial s}\frac{\partial x}{\partial h}$

若曲線族以隱函數形式 $F(x,y,s)=0$ 表示，其包絡線的隱方程，便是求下面兩個方程的解x和y之隱函數關係。

$\{\begin{array}{c}F(x,y,s)=0\\ \frac{\partial F(x,y,s)}{\partial s}=0\end{array}$

繡曲線是包絡線的例子。直線族$(A-s)x+sy=(A-s)(s)$（其中$A$是常數，$s$是直線族的變數）的包絡線為拋物線。[1] Template:Wayback

證明

設曲線族的每條曲線$C_s$為$t\mapsto (x(s,t),y(s,t))$。

設存在包絡線。由於包絡線的每點都與曲線族的其中一條曲線的其中一點相切，對於任意的$s$，設$(x(s,h(s)),y(s,h(s)))$表示$C_s$和包絡線相切的那點。由此式可見，$s$是包絡線的變數。要求出包絡線，就即要求出$h(s)$。

在$C_s$的切向量為$<\frac{\partial x}{\partial t},\frac{\partial y}{\partial t}>$，其中$t=h(s)$。

在E的切向量為$<\frac{dx}{ds},\frac{dy}{ds}>$。因為$x$是$s$和$t$的函數，而此處$t=h(s)$，局部求導有：

$\frac{dx}{ds}=\frac{\partial x}{\partial h}\frac{dh}{ds}+\frac{\partial x}{\partial s}\frac{ds}{ds}=\frac{\partial x}{\partial h}{h}^{\prime }(s)+\frac{\partial x}{\partial s}$

類似地得 $\frac{dy}{ds}=\frac{\partial y}{\partial h}{h}^{\prime }(s)+\frac{\partial y}{\partial s}$。

因為$E$和$C_s$在該點相切，因此其切向量應平行，故有

$\frac{\partial x}{\partial t}=\lambda (\frac{\partial x}{\partial h}{h}^{\prime }(s)+\frac{\partial x}{\partial s})$

$\frac{\partial y}{\partial t}=\lambda (\frac{\partial y}{\partial h}{h}^{\prime }(s)+\frac{\partial y}{\partial s})$

其中$\lambda \ne 0$。可用此兩式消去$h^{\prime }(s)$。整理後得： $\frac{\partial y}{\partial h}\frac{\partial x}{\partial s}=\frac{\partial y}{\partial s}\frac{\partial x}{\partial h}$

參考

• -{R|https://web.archive.org/web/20070621035057/http://www.math.neu.edu/~bridger/Envelope/envelope.htm}-

參見

• 克萊羅方程

外部連結

• Special Plane Curves: Envelope Template:Wayback
• Envelopes of Lines and Circles Template:Wayback