正弦-戈尔登方程

正弦-戈尔登方程是十九世纪发现的一种偏微分方程：

$φ_{t t} - φ_{x x} = \sin φ$

來自下面的拉量：

$ℒ = \frac{1}{2} (φ_{t}^{2} - φ_{x}^{2}) + \cos φ$

由于正弦-戈尔登方程有多种孤立子解而倍受瞩目。

名字是物理家熟悉的克莱因-戈尔登方程（Klein-Gordon）的雙關語。^[1]

孤立子解

利用分离变数法可得正弦-戈尔登方程的多种孤立子解。^[2]

扭型孤立子

$p 1 : = - 4 * a r c t a n ((1 / 2) * (1.5 * e x p (- 4 * s q r t (2)) - e x p (2 * x * s q r t (2))) * e x p (t - 2 - x * s q r t (2) + 2 * s q r t (2)) * s q r t (2) / (1.5 * e x p (- 4) + e x p (2 * t)))$

$p 2 : = - 4 * a r c t a n ((1 / 2) * (1.5 * e x p (2 * x * s q r t (2)) - e x p (- 4 * s q r t (2))) * e x p (t - 2 - x * s q r t (2) + 2 * s q r t (2)) * s q r t (2) / (1.5 * e x p (2 * t) + e x p (- 4)))$

钟型孤立子

正弦-戈尔登方程有如下孤立子解：

φ_{soliton} (x, t) : = 4 \arctan e^{m γ (x - v t) + δ}

其中

γ^{2} = \frac{1}{1 - v^{2}} .

双孤立子解

$p x 1 : = (8 * (1.5 * e x p (- 4) + e x p (2 * t))) * e x p (t - 2 - x * s q r t (2) + 2 * s q r t (2)) * (e x p (2 * x * s q r t (2)) + 1.5 * e x p (- 4 * s q r t (2))) / (4.50 * e x p (- 8) + 2 * e x p (4 * t) + 2.25 * e x p (2 * t - 4 - 2 * x * s q r t (2) - 4 * s q r t (2)) + 3.0 * e x p (2 * t - 4) + e x p (2 * t - 4 + 2 * x * s q r t (2) + 4 * s q r t (2)))$

$p x 2 : = - (8 * (1.5 * e x p (2 * t) + e x p (- 4))) * e x p (t - 2 - x * s q r t (2) + 2 * s q r t (2)) * (1.5 * e x p (2 * x * s q r t (2)) + e x p (- 4 * s q r t (2))) / (4.50 * e x p (4 * t) + 2 * e x p (- 8) + 2.25 * e x p (2 * t - 4 + 2 * x * s q r t (2) + 4 * s q r t (2)) + 3.0 * e x p (2 * t - 4) + e x p (2 * t - 4 - 2 * x * s q r t (2) - 4 * s q r t (2)))$

Sine-Gordon bright & dark solitons plot1

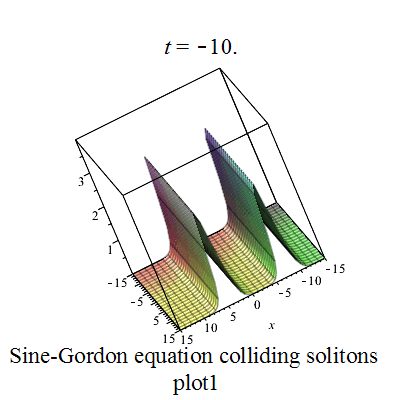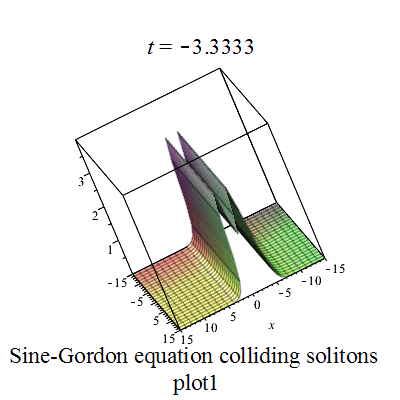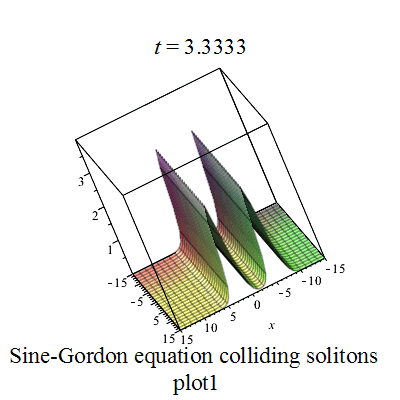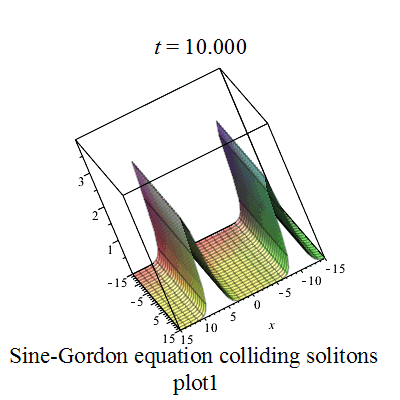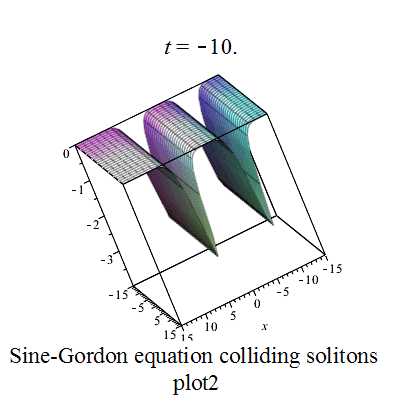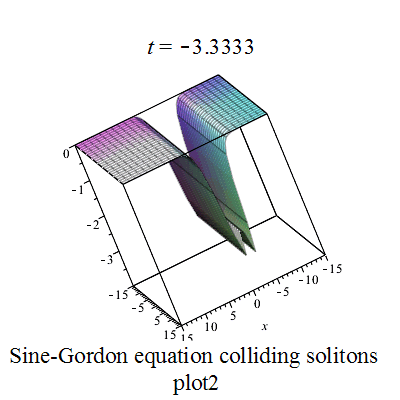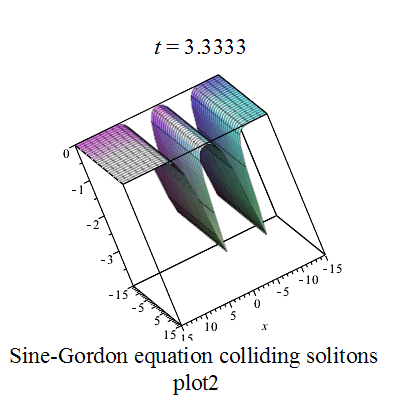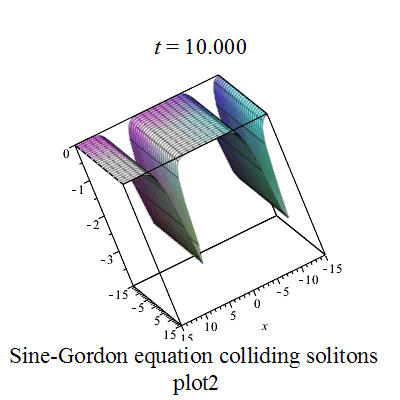三孤立子解

呼吸子解

u = 4 \arctan (\frac{\sqrt{1 - ω^{2}} \cos (ω t)}{ω \cosh (\sqrt{1 - ω^{2}} x)}),

$p z 1 : = 4 * a r c t a n ((28.460498941515413988 * (e x p (1.8973665961010275992 * x) + s q r t (e x p (3.7947331922020551984 * x)))) * s i n (O m e g a T) * c s g n (1 / c o s (O m e g a T)) * e x p (- . 94868329805051379960 * x) / (18 . + 5 . * e x p (1.8973665961010275992 * x)))$

$p z 2 : = 4 * a r c t a n ((28.460498941515413988 * (e x p (1.8973665961010275992 * x) + s q r t (e x p (3.7947331922020551984 * x)))) * s i n (O m e g a T) * c s g n (1 / c o s (O m e g a T)) * e x p (- . 94868329805051379960 * x) / (18 . + 5 . * e x p (1.8973665961010275992 * x)))$

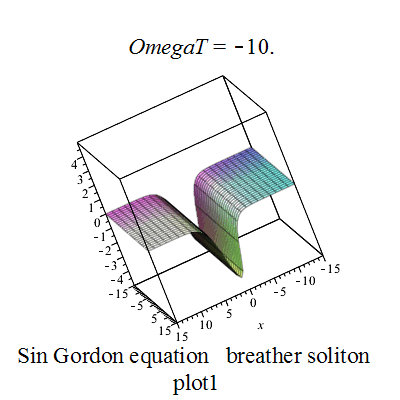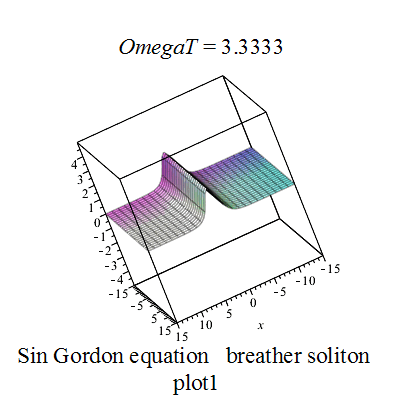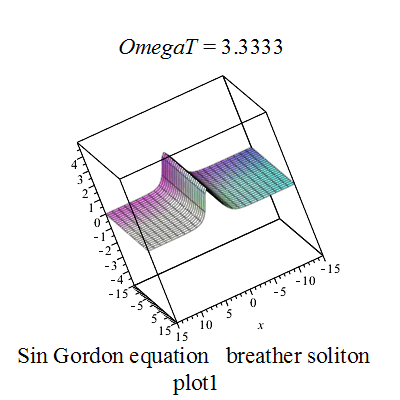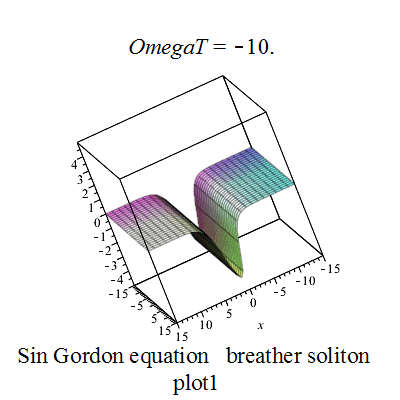几何解释

根據陳省身的研究，正弦-戈尔登方程有一个几何解释：三维欧几里德空间的负常曲率曲面（偽球面）。^[3]

正弦-戈尔登方程是：^[4]

$φ_{t t} - φ_{x x} = \sinh φ$

跟Template:Le有關。^[5]

量子場論

正弦-戈尔登是Template:Le的S對偶。

半經典量子化：^[6]

參見

瞬子
孤子
統計場論的Coulomb氣體

参考文献

↑ Template:Cite book
↑ Inna Shingareva Carlos Lizarraga Celaya, Solving Nonlinear Partial Differential Equations with Maple and Mathematica, p86-94,Springer
↑ 陈省身 Geometrical interpretation of the sinh-Gordon equation。annals Polonici Mathematici XXXIX 1981
↑ Template:Cite book
↑ Template:Cite journal
↑ Template:Cite journal

閱讀

Bour E (1862). "Théorie de la déformation des surfaces" Template:Wayback. J. Ecole Imperiale Polytechnique. 19: 1–48.
Rajaraman, R. (1989). Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory. North-Holland Personal Library. 15. North-Holland. pp. 34–45. ISBN 978-0-444-87047-6.
Polyanin, Andrei D.; Valentin F. Zaitsev (2004). Handbook of Nonlinear Partial Differential Equations. Chapman & Hall/CRC Press. pp. 470–492. ISBN 978-1-58488-355-5.
Dodd, Roger K.; J. C. Eilbeck, J. D. Gibbon, H. C. Morris (1982). Solitons and Nonlinear Wave Equations. London: Academic Press. ISBN 978-0-12-219122-0.
Georgiev DD, Papaioanou SN, Glazebrook JF (2004). "Neuronic system inside neurons: molecular biology and biophysics of neuronal microtubules". Biomedical Reviews 15: 67–75.
Georgiev DD, Papaioanou SN, Glazebrook JF (2007). "Solitonic effects of the local electromagnetic field on neuronal microtubules". Neuroquantology 5 (3): 276–291.

Template:非线性偏微分方程 Template:量子场论 Template:弦理论

[1] Template:Cite book

[2] Inna Shingareva Carlos Lizarraga Celaya, Solving Nonlinear Partial Differential Equations with Maple and Mathematica, p86-94,Springer

[3] 陈省身 Geometrical interpretation of the sinh-Gordon equation。annals Polonici Mathematici XXXIX 1981

[4] Template:Cite book

[5] Template:Cite journal

[6] Template:Cite journal

[1]

[2]

[3]

[4]

[5]

[6]

正弦-戈尔登方程

目录