有限元素法

Template:Expert 有限元素法（Template:Lang-en），即使用有限元素分析物理現象，是一种用于求解微分方程组或积分方程组数值解的數值方法。

在解偏微分方程的过程中，主要难点是如何构造一个方程来逼近原本研究的方程，并且该过程还需要保持数值稳定性。目前有许多处理的方法，他们各有利弊。当区域改变时（就像一个边界可变的固体），当需要的精确度在整个区域上变化，或者当解缺少光滑性时，有限元方法是在复杂区域（像汽车、船体结构、输油管道）上解偏微分方程的一个很好的选择。

為了解決問題，有限元素法將大型物理系統細分為更小、更簡單的部分，稱為有限元（英文：finite element）。這是通過在空間維度上進行特定的空間離散化來實現的，該離散化是通過構建對象的網格實現的：解決方案的數值域具有有限數量的點。邊值問題的有限元素法公式化最終形成了一個代數方程組。該方法在域上近似未知函數。然後，將對這些有限元建模的簡單方程式組合成一個對整個問題進行建模的較大方程式系統。然後，有限元素法通過最小化關聯的誤差函數，使用來自變異演算的變異方法來近似求解。 Template:Multiple image將整個物理系統細分為更簡單的部分具有以下優點：

• 精確表示複雜的幾何形狀。
• 可以描述多樣的材料特性。
• 輕鬆表示整體解決方案。
• 精確描述局部現象。

該方法的工作流程包括

（1）將問題的域劃分為子域的集合，每個子域由一組元素方程表示為原始問題，然後（2）系統地將所有元素方程組重組為用於最終計算的全域方程組。

在上面的第一步中，元素方程是簡化過的方程，可以局部地近似要研究的原始復雜方程組，其中原始方程通常是偏微分方程。為了求此方程式的近似解，通常將有限元素法作為伽辽金法的特例來處理。用數學語言來說，該過程是將殘差和加權函數取內積，並將該積分設為零。簡而言之，它是通過將試驗函數擬合到偏微分方程中來最小化近似誤差的過程。殘差是由試驗函數引起的誤差，權重函數是投影殘差的多項式逼近函數。該過程消除了偏微分方程中的所有空間導數，從而使偏微分方程局部近似為一組穩態問題的代數方程，或是一組用於瞬態問題的常微分方程。如果基礎偏微分方程是線性的，則元素方程也是線性的，反之亦然。穩態問題中出現的代數方程組，便利用數值線性代數方法求解，而瞬態問題中出現的常微分方程組則使用其他數值方法（例如欧拉方法或Runge-Kutta法）通過數值積分來求解。

历史

有限元法最初起源于土木工程和航空工程中的弹性和结构分析问题的研究。它的发展可以追溯到Alexander Hrennikoff（1941）和Richard Courant (1942)的工作。这些先驱者使用的方法具有很大的差异，但是他们具有共同的本质特征：利用网格离散化将一个连续区域转化为一族离散的子区域，通常叫做元.Hrennikoff的工作离散用类似于格子的网格离散区域; Courant的方法将区域分解为有限个三角形的子区域，用于求解来源于圆柱体转矩问题的二阶橢圓偏微分方程. Courant的贡献推动了有限元的发展，绘制了早期偏微分方程的研究结果。

有限元方法的发展开始于五十年代中后期使用在机身框架和结构分析上，并于六十年代通过斯图加特大学的Template:Tsl和柏克萊加州大學的Template:Tsl在土木工程中的应用工作中积累经验。

基于五十年代至六十年代大型水坝计算研究的实践经验，1965年，中国计算数学专家冯康发表了《基于变分原理的差分格式》一文，奠定了有限元计算方法的严格数学理论，为后世有限元计算方法的实际应用提供了理论保证。且Template:Or不同的是冯康教授只是从数学方面提出有限元法的。

有限元概念

单元

单元（Element）是由节点组成的几何体，如三角形单元，四面体单元等。

节点

节点（Node）是单元几何体的端点、顶点或特定点，单元的各物理量变化均体现在节点上，例如在弹性力学问题中，一个有两个节点的线单元的质量集中在两个节点上，受力也只能作用在节点上，变形也用节点的位移表示。

自由度

节点自由度（Degree of Freedom，簡寫 DoF），是节点上变量的个数，例如用位移法解结构问题时节点自由度为3，表示单个节点上三个坐标方向上的位移，又例如热分析时节点自由度为1，表示某个节点处的温度值。

网格

网格（Mesh）是由多个单元通过共用节点组成的单元网络，用以表示待解问题域。

分析方法

以下用有限元分析解决两个简单问题，更一般的问题可以类似的推导出来。

P1是一个较简单的一维问题

$\text{ P1 }:\{\begin{array}{c}{u}^{″}(x)=f(x)\text{ in }(0,1),\\ u(0)=u(1)=0,\end{array}$

其中$f$是已知函数, $u$是关于$x$的未知函数, $u^{″}$是$u$对$x$的二阶导数。

二维比较简单的问题是狄利克雷问题

$\text{P2 }:\{\begin{array}{cc}{u}_{xx}(x,y)+u_{yy}(x,y)=f(x,y)& \text{ in }\mathrm{\Omega },\\ u=0& \text{ on }\partial \mathrm{\Omega },\end{array}$

其中$\mathrm{\Omega }$是$(x,y)$平面上的连通开区域，它的边界$\partial \mathrm{\Omega }$是良好的（例如，光滑流形或多边形）, $u_{xx}$和$u_{yy}$分别表示$x$和$y$的二阶导数。问题P1能够通过计算不定积分而直接解决。然而，解决边值问题的这一方法只有在空间维数为1时才可用，并且不能推广到高维问题以及形如$u+u^{″}=f$的问题。出于这种考虑，我们将用有限元方法解决P1并将其推广至问题P2.

我们的描述分为两步，每步都反映了用有限元解决边值问题的本质。

• 将原问题描述为它的弱形式，或变分形式。这一步很少或不需要计算。
• 离散化，将弱形式在有限维空间离散化。

这两步之后，我们可以构造一个大型有限维线性方程，线性方程的解就是原边值问题的逼近解。然后，这一有限维问题由计算机求解。

弱解形式

P1的弱解形式

第一步是将问题P1和P2转化为他的等价变分形式，或弱解形式。

如果$u$是问题P1的解，那么对任何满足边界条件的光滑函数$v$ ,有

（1）$\underset{0}{\overset{1}{\int }}f(x)v(x)\mathrm{d}x=\underset{0}{\overset{1}{\int }}{u}^{″}(x)v(x)\mathrm{d}x$

相反如果 $u$对任何光滑函数$v(x)$满足$u(0)=u(1)=0$和（1），

那么$u$是P1的解。对于二次可导函数$u$证明这一点是非常容易的（利用中值定理）。

通过对（1）的右侧使用分部积分，可以得到

（2）$\begin{array}{cc}\underset{0}{\overset{1}{\int }}f(x)v(x)\mathrm{d}x& =\underset{0}{\overset{1}{\int }}{u}^{″}(x)v(x)\mathrm{d}x\\ & =u^{\prime }(x)v(x){|}_0^1-\underset{0}{\overset{1}{\int }}{u}^{\prime }(x)v^{\prime }(x)\mathrm{d}x\\ & =-\underset{0}{\overset{1}{\int }}{u}^{\prime }(x)v^{\prime }(x)\mathrm{d}x=-\varphi (u,v)\end{array}$

其中假设$v(0)=v(1)=0$。

P2的弱解形式

f當我們使用格林恆等式來表示式（2）， P2可以 $u$的積分型式表示，在此定義 $\varphi (u,v)$

$\underset{\mathrm{\Omega }}{\int }fvds=-\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }u\cdot \mathrm{\nabla }vds\equiv -\varphi (u,v),$

此處 $\mathrm{\nabla }$代表梯度，即為二維平面上的內積 。另外 $\varphi$可以轉為内积空间 $H_0^1(\mathrm{\Omega })$ ，且 $\mathrm{\Omega }$的一次微分函數 $\partial \mathrm{\Omega }$為零。我們也可以假設 $v\in H_0^1(\mathrm{\Omega })$ （詳見索伯列夫空间） 也可以顯示解的存在性和唯一性。

離散化

A function in $H_0^1,$ with zero values at the endpoints (blue), and a piecewise linear approximation (red)

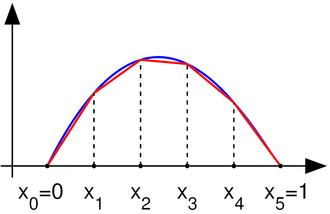
P1 和 P2 通過上述過程被离散化，並簡化為 子問題 (3)。 基本思路是將無限維線性問題替換掉：

找到 $u\in H_0^1$ 使

$\mathrm{\forall }v\in H_0^1,-\varphi (u,v)=\int fv$

表示唯有限維度的形式：

子問題(3) Find $u\in V$ such that

$\mathrm{\forall }v\in V,-\varphi (u,v)=\int fv$

此處 $V$ 是$H_0^1$的一個有限維度線性子空間。

$V$有許多可能的形式，但對於有限元素而言，在此將假定$V$存在於分段多項式函數的空間中。

對於 P1

在此在區間 $(0,1)$之中選擇 $n$個$x$的可能值 $0=x_0<x_1<\cdots <x_n<x_{n+1}=1$ 接著定義$V$ 為：

$V=\{v:[0,1]\to ℝ:v\text{ is continuous, }v{|}_{[x_k,x_{k+1}]}\text{ is linear for }k=0,\dots ,n\text{, and }v(0)=v(1)=0\}$

令e $x_0=0$ 和 $x_{n+1}=1$。觀察到在 $V$ 之中的函數根據微積分的基本定義是不可微分的。 當然，當 $v\in V$，則通常不定義 $x=x_k$，$k=1,\dots ,n$的導數，但導數事實上存在於每一個$x$的位置，並可以利用這些導數來進行部分積分運算。

兩種不同維度（二維及三維空間）的分段線性函數

對於 P2

$V$ 是屬於 $\mathrm{\Omega }$的一系列函數。 在右圖中，圖片下半部是一個15邊形的平面$\mathrm{\Omega }$的Template:Link-en，以及該多邊形的分段線性函數（圖片上半部彩色部份），即 在Template:Link-en所形成的每個三角形上呈線性； 空間$V$則由在所在的Template:Link-en的每個三角形上的函數線性組合而成。

我們希望當下面的三角形網格變得越來越精細，離散子問題（3）的解在某種意義上將收斂到原始邊界值問題P2的解。 為了測量此網格的細度，Template:Link-en由一很小的實數$h>0$所表示。此參數將與Template:Link-en中最大或平均三角形的大小有關。 當我們提高Template:Link-en的精度時（分割出更多三角形），分段線性函數的空間$V$應會隨$h$變動。因此，在某些文獻中會以$V_h$來代表。

相關條目

• 广义有限元方法
• Template:Le
• Template:Le
• Template:Le

外部链接

• MIT Video Lecture on the Finite Element Method
• Multiphysics Glossary Template:Wayback（Glossary of Multiphysics and Finite Element Modeling terms by COMSOL）
• NAFEMSTemplate:Wayback -- The International Association for the Engineering Analysis Community
• IFER Template:Wayback -- Internet Finite Element Resources - an annotated list of FEA links and programs
• Workshop "The Finite Element Method in Biomedical Engineering, Biomechanics and Related Fields" Template:Wayback
• Finite Element Analysis Resources- Finite Element news, articles and tips
• COMSOL Multiphysics Finite Element Analysis Software Template:Wayback - Official site
• CAD, Finite Element Analysis（Abaqus,Ansys）, CAE, Programming Template:Wayback- FEM, CAD, Programming, discussion forums
• Finite Element Books- books bibliography
• Mathematics of the Finite Element Method Template:Wayback
• Finite Element Methods for Partial Differential Equations Template:Wayback
• FEM AVI-gallery at CompMechLab site, St.Petersburg State Polytechnical University, Russia
• Intro to FEA
• Introduction to FEA for EM modeling（includes list of currently available software）
• Finite Element modeling of light feapowerTemplate:Dead link
• propagation Template:Wayback
• World Association of Fatigue, Durability and Fracture Mechanics - Fatigue for Finite Element Models Template:Wayback