拉東變換

拉東變換將函數 $f(x,y)$ 映射到$f(\alpha ,s)$。

本圖是將下圖做拉東變換後得到的影像，越亮的區域代表值越大，黑色的區域為0。

原始函數是白色區域為1，黑色區域為0。

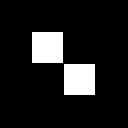
數學上，拉東變換（又稱雷登變換）是一種積分變換，這個變換將二維平面函數$f$變換成一個定義在二維空間上的一個線性函數$ℛf$($ℛf$的意思是對$f$做拉東變換)，而$ℛf$的值為函數$f$對該條線$ℛf$做積分的值。以右圖為例，黃色區域即是$f$，$A$線則是代表$ℛf$。

拉東變換是约翰·拉东在西元1917年提出，他也同時提出拉東變換的反變換公式，以及三次空間的拉東變換公式。 三次空間拉東變換，是對一個平面積分(對線積分則是Template:Link-en)。而在不久之後，更高維度的歐幾里得空間的拉東變換被提出，更詳盡的廣義拉東變換要参见Template:Link-en。 在複數上有和拉東變換相似的Template:Link-en，拉東變換被廣泛的應用在斷層掃描，拉東反變換可以從斷層掃描的剖面圖重建出投影前的函數。

簡介

若函數$f$表示一個未知的密度，對$f$做拉東變換，相當於得到$f$投影後的訊號，舉例來說：$f$相當於人體組織，斷層掃描的輸出訊號相當於經過拉東變換的$f$。 因此，可以用拉東反變換從投影後的密度函數，重建原始的密度函數，它也是重建斷層掃描的數學理論基礎，另一個被廣為人知名詞的是三維重建。

拉東變換後的訊號稱作正弦圖（Template:Lang），因為一個偏離中心的點的拉東變換是一條正弦曲線。所以對一些小點的拉東變換，會看起來像很多不同振福、相位的正弦函數重疊在一起。

拉東變換可以應用在：X射線電腦斷層掃描、條碼掃描器、Template:Link-en（Macromolecular assembly）的電子顯微鏡（例如：病毒、蛋白質複合體）、反射地震学，而且也是雙曲線偏微分方程的解。

定義

令密度函數$f(𝐱)=f(x,y)$是一個的定義域為 ${𝐑}^2$ 的緊支撐。令$ℛ$為拉東變換的運算子(operator)，則$ℛf(x,y)$是一個定義在 ${𝐑}^2$空間中的直線$L$，它的定義如下

$ℛf(L)=\underset{L}{\int }f(𝐱)|d𝐱|$

可以把直線 $L$改寫成一個弧長$z$的參數式

$(x(z),y(z))=((z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ))$

$s$是直線$L$和原點的距離，而$\alpha$是垂直於$L$的法線和$x$軸的夾角， 接下來，我們可以令$(\alpha ,s)$當作${𝐑}^2$平面上的新座標系統，把這個座標變換帶入到拉東變換得到

$\begin{array}{cc}ℛf(\alpha ,s)& =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x(z),y(z))dz\\ & =\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f((z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ))dz\end{array}$

更進一步，我們可以把${𝐑}^2$推廣到${𝐑}^n$的歐幾里得空間，對一個緊支撐的連續函數$f$做拉東變換後的函數$ℛf$是定義在 ${\mathrm{\Sigma }}_n$的超平面上，

$ℛf(\xi )=\underset{\xi }{\int }f(𝐱)d\sigma (𝐱),\mathrm{f}\mathrm{o}\mathrm{r}\xi \in {\mathrm{\Sigma }}_n$

積分的對象是自然超平面測度(natural hypersurface measure)，而$d\mathrm{\Delta }$是原本的$|d𝐱|$的高維推廣。可以觀察到對${\mathrm{\Sigma }}_n$裡的任意元素， 都是某個軌跡方程式的解

$𝐱\cdot \alpha =s.$

而$\alpha$是一個單位向量且屬於${\mathrm{S}}^{n-1}$，$s\in ℝ$，n維的拉東變換可以改寫成定義在 ${\mathrm{S}}^{n-1}\times 𝐑$上的函數

$ℛf(\alpha ,s)=\underset{𝐱\cdot \alpha =s}{\int }f(𝐱)d\sigma (𝐱)$

也可以藉由其他方式將拉東變換推廣，也就是對${𝐑}^n$的k維仿射子空間作(k-dimensional affine subspaces)積分。 而這種推廣拉東變換的特殊情況被廣泛應用在X射線電腦斷層掃描，他的做法是對一條直線積分。

與傅立葉變換的關係

拉東變換和傅立葉變換之間有很強的關聯性。單變數的傅立葉變換的定義是

$\hat{f}(\omega )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-2\pi ix\omega }dx$

而雙變數$(𝐱)=(x,y)$的傅立葉變換是

$\hat{f}(𝐰)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(𝐱)e^{-2\pi i𝐱\cdot 𝐰}dxdy$

把拉東變換的運算子的表記從$ℛ[f](s)$ 改成 $ℛ[f](\alpha ,s)$。根據投影切片定理學說，

$\widehat{{ℛ}_{\alpha }[f]}(\sigma )=\hat{f}(\sigma 𝐧(\alpha )),𝐧(\alpha )=(\cos \alpha ,\sin \alpha )$

因此一個初始函數沿著一條線傾角$\alpha$的二維的傅立葉變換，相當於對拉東變換做一維的傅立葉變換。這個結果可以推廣到n維

$\hat{f}(r\alpha )=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}ℛf(\alpha ,s)e^{-2\pi isr}ds$

對偶變換

對偶拉東變換是拉東變換的埃爾米特伴隨。令在空間${\mathrm{\Sigma }}_n$上的函數$g$，而對偶拉東變換的運算子定義為${ℛ}^{*}$。作用在$g$上

${ℛ}^{*}g(x)=\underset{x\in \xi }{\int }g(\xi )d\mu (\xi )$

積分的範圍是所有和$x\in {𝐑}^2$相交的超平面集合，而測度(measure)$d\mu$是集合$\xi |x\in \xi$特殊的機率測度(Probability measure)， 當對著$x$旋轉時，$d\mu$的值不會改變

對於一個二維的拉東變換，其對偶變換是

${ℛ}^{*}g(x)=\frac{1}{2\pi }\underset{\alpha =0}{\overset{2\pi }{\int }}g(\alpha ,𝐧(\alpha )\cdot 𝐱)d\alpha$

在影像處理的文章中，對偶變換經常被稱作反向投影(back-projection) ，因为它将平面中每条线上定义的函数 投影到该线上，从而生成图像。

交結性質

根據拉普拉斯算子$\mathrm{\Delta }$在 ${𝐑}^n$的定義是

$\mathrm{\Delta }=\frac{{\partial }^2}{\partial x_1^2}+\cdots +\frac{{\partial }^2}{\partial x_n^2}$

這是一個旋轉不變性的二階微分算子，在空間${\mathrm{\Sigma }}_n$，半徑的二階導數

$Lf(\alpha ,s)\equiv \frac{{\partial }^2}{\partial s^2}f(\alpha ,s)$

也是旋轉不變性。 而拉東變換與其對偶變換屬於交結運算子(intertwining operator)，是因為

$ℛ(\mathrm{\Delta }f)=L(ℛf),{ℛ}^{*}(Lg)=\mathrm{\Delta }({ℛ}^{*}g)$

重建方法

重建處理是指從投影影像重建一個影像，或是一個函數$f$。重建處理是一種逆問題(inverse problem)。

拉東反變換公式

對於二維拉東變換，最常被使用的解析公式(analytical formula)$f$，是Filtered Backprojection Formula或拉東反變換公式，反變換公式為

$f(𝐱)=\underset{0}{\overset{\pi }{\int }}(ℛf(\cdot ,\theta )*h)(⟨𝐱,{𝐧}_{\theta }⟩)d\theta$

函數$h$滿足$\hat{h}(k)=|k|$，卷積核 (convolution kernel) $h$在一些文章中稱作Ramp filter。

不適定問題 (ill-posedness)

直覺上，反變換公式應該和微分類似，$\widehat{\frac{d}{dx}}f(x)=ik\hat{f}(k)$。我們可以看的出來反變換公式 的行為類似微分。大致上來說，這個反變換公式把目標奇異化(singular)；要如何量化拉東反轉化的不適定問題 (ill-posedness)呢？首先可以寫出

$\widehat{{ℛ}^{*}ℛg}(k)=\frac{1}{||𝐤||}\hat{g}(𝐤)$

${ℛ}^{*}$即是前面定義的反變換運算子，且伴隨著(adjoint to)拉東變換，因此$g(𝐱)=e^{i⟨{𝐤}_0,𝐱⟩}$，上式變成

${ℛ}^{*}ℛg=\frac{1}{||𝐤||}{e}^{i⟨{𝐤}_0,𝐱⟩}$

複數指數函數$e^{i⟨{𝐤}_0,𝐱⟩}$，是${ℛ}^{*}ℛ$的固有函數 (eigenfunction) ， 而特徵值 (eigenvalue)為$\frac{1}{||𝐤||}$。$ℛ$的奇異值 (singular values) 是$\sqrt{\frac{1}{||𝐤||}}$， 因為這些奇異值 (singular values)會趨近於0，所以${ℛ}^{-1}$是無界的(unbounded) 。

反變換公式

外顯(explicit)且計算效率好的拉東反變換公式，以及他的對偶是存在的。n維的反拉東變換可以由

$c_{n}f=(-\mathrm{\Delta }{)}^{(n-1)/2}{ℛ}^{*}\{ℛf\}$

其中

$c_n=(4\pi {)}^{(n-1)/2}\frac{\mathrm{\Gamma }(n/2)}{\mathrm{\Gamma }(1/2)}$

而$\mathrm{\Delta }$是拉普拉斯算子(Laplacian)，$(-\mathrm{\Delta }{)}^{(n-1)/2}$是偽微分算子(pseudodifferential operator)

$ℱ[(-\mathrm{\Delta }{)}^{(n-1)/2}\varphi ](\xi )=|2\pi \xi {|}^{n-1}ℱ\varphi (\xi ).$

$ℱ$是傅立葉變換的運算子(operator)。

參見

• 反摺積
• Template:Le
• Template:Le
• 霍夫變換
• 疊代稀疏漸近最小方差算法

參考

• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Springer.
• Template:Citation
• Template:Citation.
• Template:Citation; Translation: Template:Citation.
• Template:Springer.
• Template:MathWorld.