譜序列

在同調代數中，譜序列是一種藉著逐步逼近以計算同調或上同調群的技術，由讓·勒雷在1946年首創。其應用見諸代數拓撲、群上同調與同倫理論。

動機

讓·勒雷當初為了研究代數拓撲學，而引入層的概念，從而面臨計算層上同調的問題。為此，勒雷發明了現稱勒雷譜序列的計算方法，它聯繫了一個層的上同調群與其正像的上同調群。

人們很快就發現：勒雷譜序列只是一個特例。譜序列還現身於纖維化等幾何問題；更抽象地說，對合成函子取導函子也會得到譜序列，稱為格羅滕迪克譜序列。雖然導範疇在理論層面提供了較簡鍊的框架，譜序列仍是最有效的計算工具。

由於譜序列包含大量的項，實際計算時往往會陷入帶（至少）三重指標的群或模的迷陣。在許多實際狀況中，譜序列最後會「塌陷」，此時譜序列可以給出明確的資訊。若譜序列不塌陷，則須靠一些竅門取得有用的資訊。

形式定義

以下固定一個阿貝爾範疇 $𝒜$，常見例子是一個環上的模範疇。譜序列是一個非負整數 $r_0$ 及下述資料：

• 對所有整數 $r\ge r_0$，有範疇中的一個對象 $E_r$。
• 自同態 $d_r:E_r\to E_r$，滿足 $d_r^2=0$，稱為邊界映射或微分。
• 從 $E_{r+1}$ 到 $H(E_r,d_r)$ 的同構。

通常省去 $E_{r+1}$ 與 $H(E_r,d_r)$ 的同構，而寫成等式。

最基本的例子是鏈複形 $C_{\bullet }$，它帶有一個微分 $d$。取 $r_0=0$，並令 $E_0=C_{\bullet }$，於是必有 $E_1=H(C_{\bullet })$；這個新鏈複形上的微分只有一個自然的選擇，就是零映射。於是有 $E_1=E_2=\cdots$。綜之，我們得到一個鏈複形範疇上的譜序列：

• $E_0=C_{\bullet }$
• $E_r=H(C_{\bullet })(r\ge 1)$

由於只有 $r=0$ 時微分映射才可能非零，此序列在第一步後就不含任何新資訊。

較常見的是雙分次模（或層）範疇上的譜序列，表作 $E_r^{p,q}$，此時的微分映射次數與 $r$ 有關：對於上同調譜序列，$d_r:E_r\to E_r$ 的次數是 $(r,-r+1)$。對於同調譜序列，通常將各項寫成 $E_r$，微分映射 $d^r:E_r\to E_r$ 的次數是 $(-r,r-1)$。

譜序列之間的態射 $f:E\to E^{\prime }$ 定義為一族態射 $f_r:E_r\to {E_r}^{\prime }$，使之與同構 $E_{r+1}\simeq H(E_r,d_r)$ 交換。譜序列對此構成了一個阿貝爾範疇。

正合偶

交換代數中大部分的譜序列來自鏈複形，而已知構造譜序列最有力的方法是 William Massey 的正合偶。正合偶在代數拓撲學中很常見，此時對於許多譜序列，正合偶是唯一已知的構造法。事實上，正合偶可以用來構造所有已知的譜序列。

同樣固定一個阿貝爾範疇（通常取一個環上的雙分次模）$𝒜$，一個正合偶是：

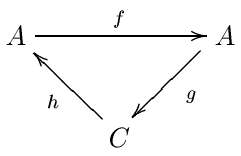
• 一對對象 $A,C$
• 三個態射：
  • $f:A\to A$
  • $g:A\to C$
  • $h:C\to A$

使之滿足下述正合條件：

• Image f = Kernel g
• Image g = Kernel h
• Image h = Kernel f

將這組資料簡記為 $(A,C,f,g,h)$。正合偶通常以三角形表示。$C$ 對應到譜序列的 $E_0$ 項，而 $A$ 是一些輔助資料。

為了得到譜序列的後續項，以下將構造導出偶。令：

• $d:=g\circ h$
• $A^{\prime }:=f(A)$
• $C^{\prime }:=\mathrm{K}\mathrm{e}\mathrm{r}(d)/\mathrm{I}\mathrm{m}(d)$
• $f^{\prime }:=f{|}_{A^{\prime }}$
• $h^{\prime }:C^{\prime }\to A^{\prime }$ 由 $h$ 導出。
• $g^{\prime }:A^{\prime }\to C^{\prime }$ 定義如下：若 $𝒜$ 為某個環上的模範疇，對任一 $a\in A^{\prime }$，存在 $b\in A^{\prime }$ 使得 $a=f(b)$，定義 $g^{\prime }(a)$ 為 $g(b)$ 在 $C^{\prime }$ 中的像。一般而言，可利用 Mitchell 嵌入定理構造態射 $g^{\prime }$。

現在可以驗證 $(A^{\prime },C^{\prime },f^{\prime },g^{\prime },h^{\prime })$ 構成正合偶。$C^{\prime }$ 對應到譜序列的 $E_1$ 項。續行此法，可以得到一族正合偶 $(A^{(n)},C^{(n)},f^{(n)},g^{(n)},h^{(n)})$。相應的譜序列定義為 $E_n:=C^{(n)}$，$d_n:=g^{(n)}\circ h^{(n)}$。

圖解

譜序列的 E₂ 項

一個雙分次譜序列含有大量要追蹤的資訊，不過有個常見的圖解法有助於闡明其結構。以下取上同調譜序列為例。在此有三個指標 $r,p,q$。對每個 $r$，設想有一張方格紙，分別讓 $p,q$ 對應於橫、縱軸。每一個格子點 $(p,q)$ 對應到對象 $E_r^{p,q}$。微分 $d_r$ 的次數為 $(r,-r+1)$，方向如圖所示。

收斂與退化

在第一個簡單的例子中，譜序列在 $r\ge 1$ 後的微分映射皆為零，故不再改變。這時可定義該譜序列的極限為 $E_{\mathrm{\infty }}:=E_r(r\ge 1)$。對於一般的譜序列，也往往存在一個極限，極限與各項的關係可說是譜序列的眾妙之門。

定義：若譜序列 $E_r^{p,q}$ 對每個 $(p,q)$ 都存在 $r(p,q)\in \mathbb{N}$，使得當 $r\ge r(p,q)$ 時，$d_r^{p-r,q+r-1}:E_r^{p-r,q+r-1}\to E_r^{p,q}$ 及 $d_r^{p,q}:E_r^{p,q}\to E_r^{p+r,q-r+1}$ 皆為零，則稱 $E_r^{p,q}$ 之極限項為 $E_{\mathrm{\infty }}^{p,q}:=E_r^{p,q}$（取充分大的 $r$）。最常見的例子是集中在第一象限的譜序列，此時極限項恆存在。

其中的指標 $p$ 指涉過濾結構。

若存在對象 $E^{\bullet }$、過濾結構 $\cdots \subset F^{p+1}{E}^{\bullet }\subset F^p{E}^{\bullet }\subset \cdots$，及一族同構 ${\beta }^{p,q}:E_{\mathrm{\infty }}^{p,q}\simeq {\mathrm{g}\mathrm{r}}^p{E}^{p+q}$，滿足 $\bigcap _p{F}^p{E}^{\bullet }=(0),\bigcup _p{F}^p{E}^{\bullet }=E^{\bullet }$（這種過濾稱為「正則過濾」），則稱 $E_r^{p,q}$ 收斂到 $E^{\bullet }$，通常表為下述符號：

$E_r^{p,q}{\Rightarrow }_p{E}_{\mathrm{\infty }}^{p,q}$

習慣上，人們也常將左式寫成 $E_2^{p,q}$，因為譜序列中最重要的頁往往是 $E_2^{p,q}$。

最簡單的收斂特例是退化：

定義：固定 $r\in \mathbb{N}$，若對每個 $s\ge r$，微分映射 $d_s$ 都是零，則稱該譜序列在第 $r$ 頁退化。

退化性保證了 $E_r\simeq E_{r+1}\simeq \cdots$，此時 $E_r$ 即其極限。如果一個雙分次譜序列 $E_r^{p,q}$ 的非零項集中於某一條水平或垂直線上，則必在 $r=2$ 時退化。

例子

過濾結構導出的譜序列

最常見的譜序列之一來自帶有過濾結構的對象，通常是鏈複形或上鏈複形。這是一個對象 $C$ 及微分映射 $d:C\to C$ ，使之滿足 $d^2=0$，以及

$C=F^{0}C\supset F^{1}C\supset \cdots F^{n}C\supset F^{n+1}C=0$

$d{F}^{p}C\subset F^{p}C$

同調群上也有相應的過濾

$F^{p}H(C,d):=\mathrm{I}\mathrm{m}(H(F^{p}C,d)\to H(C,d)$

對此，定義相應的分次對象

${\mathrm{g}\mathrm{r}}_{F}C:=\underset{p\ge 0}{⨁}{F}^{p}C/F^{p+1}C$

${\mathrm{g}\mathrm{r}}_{F}H(C):=\underset{p\ge 0}{⨁}{F}^{p}H(C)/F^{p+1}H(C))$

取微分映射為零，可視之為複形。

以下式定義譜序列：

$Z_r^p:=x\in F^{p}C:dx\in F^{p+r}C$

$E_r^p:=Z_r^p/(d{Z}_{r-1}^{p-r+1}+Z_{r-1}^{p+1})=Z_r^p/(Z_r^p\cap (d{F}^{p-r+1}C+F^{p+1}C))$

此時有 $E_0^p=F^{p}C/F^{p+1}C,E_1^p=H({\mathrm{g}\mathrm{r}}^{p}C)$，且譜序列收斂：

$E_r^p\Rightarrow E_{\mathrm{\infty }}^p={\mathrm{g}\mathrm{r}}^{p}H(C)$

通常也寫成 $E_r\Rightarrow H(C)$。

取 $𝒜$ 為取值在某個阿貝爾範疇中的上鏈複形範疇。此時的對象 $C$ 是個上鏈複形 $\cdots \to C^q\to C^{q+1}\to \cdots$，$d$ 是上鏈複形的微分映射。上述譜序列帶有三個指標 $p,q,r$，並可進一步化成下述形式：

$E_0^{p,q}=F^p{C}^{p+q}/F^{p+1}{C}^{p+q}$

$E_1^{p,q}=H^{p+q}({\mathrm{g}\mathrm{r}}^p{C}^{\bullet })$

$E_{\mathrm{\infty }}^{p,q}={\mathrm{g}\mathrm{r}}^p(H^{p+q}(C^{\bullet }))$

雙複形的譜序列

以下考慮取值在某個阿貝爾範疇中的雙複形，即一組對象 $C^{p,q}$，及兩組微分映射 $d^{\prime }:C^{p,q}\to C^{p+1,q}$ 及 $d^{″}:C^{p,q}\to C^{p,q+1}$，滿足

$d{\text{'}}^2=d^{\prime }{\text{'}}^2=0$

$d^{\prime }{d}^{″}+d^{″}{d}^{\prime }=0$

對一個雙複形，可定義其全複形 $(C,D)$（也記為 $T(C)$ 或 $\mathrm{T}\mathrm{o}\mathrm{t}(C)$） 為

$C^n:=\underset{p+q=n}{⨁}{C}^{p,q}$

$D:=d^{\prime }+d^{″}$

$C$ 上有兩組過濾，分別是：

${(}^{\prime }{F}^{p}C{)}^n:=\underset{i+j=n,i\ge p}{⨁}{C}^{i,j}$

${(}^{″}{F}^{q}C{)}^n:=\underset{i+j=n,j\ge q}{⨁}{C}^{i,j}$

它們給出兩個譜序列 $E_r$ 與 $E_r$。首先計算 $E_0{,}^{\prime }{E}_1{,}^{\prime }{E}_2$ 項：

$E_0^{i,j}=C^{i,j}$

$E_1^{i,j}=H_{d^{″}}^j(C^{i,\bullet })$

$E_2^{i,j}=H_{d^{\prime }}^i(H_{d^{″}}^j(C^{\bullet ,\bullet }))$（即：先取縱向上同調，再取橫向上同調）

同理可計算 $E_0{,}^{″}{E}_1{,}^{″}{E}_2$：

$E_0^{i,j}=C^{j,i}$

$E_1^{i,j}=H_{d^{\prime }}^j(C^{\bullet ,i})$

$E_2^{i,j}=H_{d^{″}}^i(H_{d^{\prime }}^j(C^{\bullet ,\bullet }))$（即：先取橫向上同調，再取縱向上同調）。

這兩個譜序列通常是不同的，但隨著 $r$ 增大，它們都收斂到 $H(C)$，由此可以得到一些有趣的比較定理。

例子

Tor函子的交換性

利用譜序列，可以迅速導出Tor函子的交換性，即一自然同構：

${\mathrm{T}\mathrm{o}\mathrm{r}}_i(M,N)={\mathrm{T}\mathrm{o}\mathrm{r}}_i(N,M)$

取定平坦分解 $P_{\bullet }\to M\to 0$ 及 $Q_{\bullet }\to N\to 0$。視之為集中於正項的複形，其微分映射分別記為 $d,e$。考慮雙複形 $C_{i,j}:=P_i\otimes Q_j$，其微分映射定義為 $d_{i,j}:=d_i\otimes \mathrm{i}\mathrm{d}+(-1{)}^j\mathrm{i}\mathrm{d}\otimes e_j$（以使微分映射滿足反交換性）。取其譜序列，遂得到：

$E_{p,q}^2=H_p^I(H_q^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_p^I(P_{\bullet }\otimes H_q^{II}(Q_{\bullet }))$

$E_{p,q}^2=H_q^{II}(H_p^I(P_{\bullet }\otimes Q_{\bullet }))=H_q^{II}(Q_{\bullet }\otimes H_p^I(P_{\bullet }))$

由於複形 $P_{\bullet },Q_{\bullet }$ 是平坦分解，其同調群只集中在零次項，此時其表示式為：

$H_p^I(P_{\bullet }\otimes N)={\text{Tor}}_p(M,N)$

$H_q^{II}(Q_{\bullet }\otimes M)={\text{Tor}}_q(N,M)$

故 $E_{p,q}^2$ 只在 $p=0$ 上有非零項，而 $E_{p,q}^2$ 只在 $q=0$ 上有非零項，這保證了譜序列在第二頁退化，由此導出同構：

${\text{Tor}}_p(M,N)\cong E_{p,q}^{\mathrm{\infty }}={\text{gr}}_p{H}^{p+q}(T(C_{\bullet ,\bullet }))$

${\text{Tor}}_q(N,M)\cong E_{p,q}^{\mathrm{\infty }}={\text{gr}}_q{H}^{p+q}(T(C_{\bullet ,\bullet }))$

當 $p=q$ 時，上述等式的右項同構（雖然其分次結構不同），由此得到 Tor 的交換性。

示性數

運用譜序列時，通常會假設某些項為零，或假設譜序列在第一或第二頁退化。但有時儘管對各項及微分映射一無所知，仍可從譜序列中萃取資訊，最簡單的例子是示性數：固定一個阿貝爾範疇 $𝒜$ 及一個交換群 $C$，所謂示性數是一個函數 $\chi :\mathrm{O}\mathrm{b}𝒜\to C$，滿足：

• $\mathrm{\forall }0\to Y\to X,\chi (X)=\chi (Y)+\chi (X/Y)$
• $X\simeq Y\Rightarrow \chi (X)=\chi (Y)$

例如：取 $𝒜$ 為某個域 $k$ 上的有限維向量空間範疇，則 $\chi :V\mapsto {\dim }_{k}V$ 是一個示性數。

對任一 $𝒜$ 上的有限複形 $K^{\bullet }$，定義

$\chi (K^{\bullet })=\sum _i(-1{)}^i\chi (K^i)$

容易證明 $\chi (K^{\bullet })=\sum _i(-1{)}^i\chi (H^i(K^{\bullet }))$。考慮任一在 $𝒜$ 上的收斂譜序列 $(E_r^{\bullet })$，由於譜序列的每一頁都是前一頁的同調，遂得到

$\chi (E_r^{\bullet })=\chi (E_{r+1}^{\bullet })=\cdots =\chi (E_{\mathrm{\infty }}^{\bullet })$

然而

$\chi (E^n)=\sum _p\chi (F^p{E}^n/F^{p+1}{E}^n)=\sum _p\chi (E_{\mathrm{\infty }}^{p,n-p})$

於是得到

$\mathrm{\forall }r,\sum _n(-1{)}^n\chi (E^n)=\chi (E_r^{\bullet })$

參考資料

歷史文獻

• Template:Cite journal
• Template:Cite journal
• Template:Cite journal
• Template:Cite journal
• Template:Cite journal

當代文獻

• Template:Springer
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite journal