截角大十二面體

Template:NoteTA Template:Infobox polyhedron 在幾何學中，截角大十二面體是一種具有二十面體對稱非凸均勻多面體，由24個面組成，其結構可以視為切去大十二面體的12個頂點而得，其具有12對互相平行面，因此也可以視為一種平行多面體，其對偶多面體為小星形五角化十二面體。

分類

1993年，茲維·喀拉·埃爾發表的論文《Uniform Solution for Uniform Polyhedra》中，將截角大十二面體編號為K₄₂，表示其為一個二十面體對稱的多面體，同一年，馬德爾參考茲維·喀拉·埃爾的分類方式，將截角大十二面體給予索引編號U₃₇。其也被考克斯特的論文收錄，並給予編號C₄₇。溫尼爾也在他的書《多面體模型》中將之給予編號W₇₅。

性質

截角大十二面體由24個面、90條邊和60個頂點組成，是一種二十四面體。每個頂點都是2個十邊形和1個五角星的公共頂點。

面的組成

截角大十二面體由24個面組成，在其二十四個面中，有12個五角星面和12個十邊形面，其中有12個面是非凸面。

二面角

截角大十二面體有兩種二面角，包括了十邊形-十邊形二面角和十邊形-五角星二面角。其中十邊形-十邊形二面角為五平方根倒數的反餘弦值；十邊形-五角星二面角為負的五平方根倒數之反餘弦值。

${\text{Angle}}_{\left\{10\right\},\left\{10\right\}}={\cos }^{-1}\frac{\sqrt{5}}{5}\approx 63.434948823^{\circ }$

${\text{Angle}}_{\left\{10\right\},\{{}^5/{}_2\}}={\cos }^{-1}\frac{-\sqrt{5}}{5}\approx 116.565051177^{\circ }$

其中$\left\{10\right\},\{{}^5/{}_2\}$為十邊形和五角星的施萊夫利符號。

頂點座標

邊長長度為1單位且幾何中心位於原點的截角大十二面體，其頂點座標為

$(\pm \frac{1}{2},0,\pm \frac{5+\sqrt{5}}{4})$、

$(\pm \frac{5+\sqrt{5}}{4},\pm \frac{1}{2},0)$、

$(0,\pm \frac{5+\sqrt{5}}{4},\pm \frac{1}{2})$、

$(\pm \frac{1+\sqrt{5}}{4},\pm \frac{1}{2},\pm \frac{1+\sqrt{5}}{2})$、

$(\pm \frac{1+\sqrt{5}}{2},\pm \frac{1+\sqrt{5}}{4},\pm \frac{1}{2})$、

$(\pm \frac{1}{2},\pm \frac{1+\sqrt{5}}{2},\pm \frac{1+\sqrt{5}}{4})$、

$(\pm \frac{3+\sqrt{5}}{4},\pm \frac{\sqrt{5}\pm 1}{4},\pm \frac{3+\sqrt{5}}{4})$、

$(\pm \frac{3+\sqrt{5}}{4},\pm \frac{3+\sqrt{5}}{4},\pm \frac{\sqrt{5}\pm 1}{4})$、

$(\pm \frac{\sqrt{5}\pm 1}{4},\pm \frac{3+\sqrt{5}}{4},\pm \frac{3+\sqrt{5}}{4})$。

相關多面體

截角大十二面體的頂點布局與多種多面體相同。其中三種為均勻多面體相同，分別為非凸大斜方截半二十面體、大十二面截半二十面體和大斜方十二面體；還有2種複合多面體，分別是Template:Link-en和Template:Link-en。

非凸大斜方截半二十面體	大十二面截半二十面體	大斜方十二面體
截角大十二面體	Template:Link-en	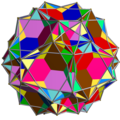Template:Link-en

這個多面體是大十二面體經過截角變換後的結果，大十二面體在不同的截角深度也得到有不同的結果，例如節到中點後得到截半大十二面體，過截角後得到的立體則與對偶多面體的截角等價，為截角小星形十二面體。這種多面體外觀與正二十面體幾乎一樣，但其有24個面，12個面是來自截角後的頂點以及12個截角的五角星與之重合。

名稱	小星形十二面體	截角小星形十二面體	截半大十二面體	截角大十二面體	大十二面體
Template:Link-en	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD
圖像

對偶複合體

小星形五角化十二面體與其對偶的複合體為複合截角大十二面體小星形五角化十二面體 。其共有84個面、180條邊和84個頂點，其尤拉示性數為-12，虧格為7，有12個非凸面。

參見

• 大十二面體

外部連結

• Template:Mathworld