伽利略变换

伽利略變換（Template:Lang-en）是-{zh-cn:经典力学; zh-hk:經典力學; zh-tw:古典力學}-中用以在兩個只以匀速相對移動的參考系之間變換的方法，屬於一種被動態變換。在相對論效應下，伽利略变换在物體以接近光速運動时不成立^[1]，在電磁系統中也不会成立。^[2]

伽利略·伽利莱在解釋匀速運動時制定了這一套概念。^[3]他用其解釋球體滾下斜面這一力學問題，並測量出地球表面引力加速度的數值。

在狭义相对论中，伽利略变换被庞加莱变换所取代；相反，庞加莱变换的经典极限c →∞中的群收缩产生了伽利略变换。

平移

伽利略變換建基於人們加減物體速度的直覺。在其核心，伽利略變換假設時間和空間是絕對的。

這項假設在洛伦兹变换中被捨棄，因此就算在相對論性速度下，洛伦兹变换也是成立的；而伽利略變換則是洛伦兹变换的低速近似值。

以下為伽利略變換的數學表達式，其中 $(x, y, z, t)$ 和 $(x^{'}, y^{'}, z^{'}, t^{'})$ 分別為同一個事件在兩個坐標系 $S$ 和 $S^{'}$ 中的坐標。兩個坐標系以相對匀速運行（速度為 $v$ ），運行方向為 $x$ 和 $x^{'}$ ，原點在時間 $t = t^{'} = 0$ 時重合。 ^[4] ^[5] ^[6] ^[7]

x^{'} = x - v t

y^{'} = y

z^{'} = z

t^{'} = t

最後一條方程式意味著時間是不受觀測者的相對運動影響的。

利用線性代數的術語來說，這種變換是個錯切，是矩陣對向量進行變換的一個過程。當參考系只沿著x軸移動時，伽利略變換只作用於兩個分量：

(x^{'}, t^{'}) = (x, t) (\begin{matrix} 1 & 0 \\ - v & 1 \end{matrix}) .

雖然在伽利略變換中沒有必要用到矩陣表達法，但是用了矩陣就可以和狹義相對論中的變換法進行比較。

三種伽利略變換

沿著一個加速中觀測者的世界線所看到的時空。

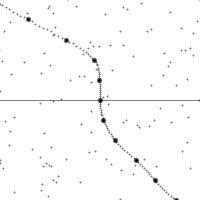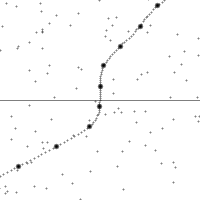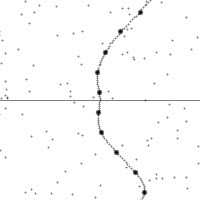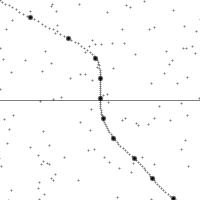
縱軸為時間，橫軸為距離，虛線為觀測者在時空中的軌跡。圖的下半部是已經發生了的事件，上半部則是未來的事件。圖中小點為時空中的事件。

世界線的斜率為觀測者的相對速率。注意觀測者在加速時所看到的時空會進行錯切。

伽利略變換可以唯一寫成由時空的旋轉、平移和匀速運動複合而成的函數。^[8]設x為三維空間中的一點，t為一維時間中的一點。時空當中的任何一點可以表達為有序對(x,t)。速度為v的匀速運動表達為 $(𝐱, t) \mapsto (𝐱 + t 𝐯, t)$ ，其中v在R³內。平移表達為 $(𝐱, t) \mapsto (𝐱 + 𝐚, t + b)$ ，其中a在R³內，b在R內。旋轉表達為 $(𝐱, t) \mapsto (G 𝐱, t)$ ，其中Template:Nowrap為某正交變換。^[8]作為一個李群，伽利略變換的維度為10。^[8]

这三种变换可更加数学化地表达为伽利略群^[9]。首先G为SO(3)中的旋转矩阵，3维内积在G的作用下保持不变，表达为: $< G \vec{x}, G \vec{y} > = < \vec{x}, \vec{y} >$ 设在某t时刻有映射 $φ_{t} (\vec{a}, \vec{b}, G)$ 将空间上的某一点x映射到另一点 $G \vec{x} + \vec{a} + \vec{b} \cdot t$ 上。可证得 $φ_{t}$ 构成一个群。
结合律： $φ_{t}$ 为线性映射，线性映射满足结合律。

单位元： $φ_{t} (\vec{0}, \vec{0}, 𝐈) (\vec{x}) = \vec{x}$

逆映射： $φ_{t} (\vec{a}, \vec{b}, G)^{- 1} = φ_{t} (- G^{- 1} \vec{a}, - G^{- 1} \vec{b}, G^{- 1})$

封闭性： $\begin{matrix} φ_{t} (\vec{a^{'}}, \vec{b^{'}}, G^{'}) \circ φ_{t} (\vec{a}, \vec{b}, G) (\vec{x}) = G G^{'} \vec{x} + (G^{'} \vec{a} + \vec{a^{'}}) + (G \vec{b} + \vec{b^{'}}) \cdot t \\ = φ_{t} (G^{'} \vec{a} + \vec{a^{'}}, G \vec{b} + \vec{b^{'}}, G G^{'}) (\vec{x}) \end{matrix}$ 对应的有：
空间平移： $φ_{t} (\vec{a}, \vec{0}, 𝐈) (\vec{x}) = \vec{x} + \vec{a}$
速度变换： $φ_{t} (\vec{0}, \vec{b}, 𝐈) (\vec{x}) = \vec{x} + \vec{b} \cdot t$
空间旋转： $φ_{t} (\vec{0}, \vec{0}, G) (\vec{x}) = G \vec{x}$
$φ_{t} (\vec{a}, \vec{b}, G)$ 为不含时伽利略群，加上时间平移 $t \mapsto t + t_{0}$ 后映射 $(\vec{x}, t) \mapsto (φ_{t}, t + t_{0}) = (G \vec{x} + \vec{a} + \vec{b} \cdot t, t + t_{0})$ 构成一个完整伽利略群，其依旧满足群的性质。完整伽利略群具有10个生成元，分别为3个空间平移(x,y,z)，3个空间转动(对应3个坐标基矢），3个速度，以及一个时间平移。

伽利略群的中心擴張

這裡我們只考慮伽利略群的李代數。結果能夠輕易延伸到李群。L的李代數由H、P_i、C_i和L_ij張成（反對稱張量），並能夠受交換子的作用，其中

[H, P_{i}] = 0

[P_{i}, P_{j}] = 0

[L_{i j}, H] = 0

[C_{i}, C_{j}] = 0

[L_{i j}, L_{k l}] = i [δ_{i k} L_{j l} - δ_{i l} L_{j k} - δ_{j k} L_{i l} + δ_{j l} L_{i k}]

[L_{i j}, P_{k}] = i [δ_{i k} P_{j} - δ_{j k} P_{i}]

[L_{i j}, C_{k}] = i [δ_{i k} C_{j} - δ_{j k} C_{i}]

[C_{i}, H] = i P_{i}

[C_{i}, P_{j}] = 0 .

H為時間平移的生成元（哈密顿算符），P_i為平移的生成元（動量算符），C_i為伽利略變換的生成元，而L_ij為旋轉的生成元（角動量算符）。

現在我們可以對H'、P'_i、C'_i、L'_ij（反對稱張量）、M所張成的李群進行中心擴張，使得M與一切都可交換（位於中心，「中心擴張」因此得名）：

[H^{'}, P'_{i}] = 0

[P'_{i}, P'_{j}] = 0

[L'_{i j}, H^{'}] = 0

[C'_{i}, C'_{j}] = 0

[L'_{i j}, L'_{k l}] = i [δ_{i k} L'_{j l} - δ_{i l} L'_{j k} - δ_{j k} L'_{i l} + δ_{j l} L'_{i k}]

[L'_{i j}, P'_{k}] = i [δ_{i k} P'_{j} - δ_{j k} P'_{i}]

[L'_{i j}, C'_{k}] = i [δ_{i k} C'_{j} - δ_{j k} C'_{i}]

[C'_{i}, H^{'}] = i P'_{i}

[C'_{i}, P'_{j}] = i M δ_{i j}

參見

備註

Template:Reflist

Template:Relativity

↑ Template:Cite web
↑ Template:Cite book
↑ Galileo 1638 Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze 191 - 196, published by Lowys Elzevir (Louis Elsevier), Leiden, or Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914, reprinted on pages 515-520 of On the Shoulders of Giants: The Great Works of Physics and Astronomy. Stephen Hawking, ed. 2002 ISBN 978-0-7624-1348-5
↑ Template:Citation, Chapter 2 §2.6, p. 42 Template:Wayback
↑ Template:Citation, Chapter 38 §38.2, p. 1046,1047 Template:Wayback
↑ Template:Citation, Chapter 9 §9.1, p. 261 Template:Wayback
↑ Template:Citation, Chapter 5, p. 83 Template:Wayback
↑ ^8.0 ^8.1 ^8.2 Template:Cite book
↑ H.R.Petry,B.Metsch; Theoretische Mechanik (Oldenburg, München 2005) 第18页 ISBN 3-486-24673-9

[1] Template:Cite web

[2] Template:Cite book

[3] Galileo 1638 Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze 191 - 196, published by Lowys Elzevir (Louis Elsevier), Leiden, or Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914, reprinted on pages 515-520 of On the Shoulders of Giants: The Great Works of Physics and Astronomy. Stephen Hawking, ed. 2002 ISBN 978-0-7624-1348-5

[4] Template:Citation, Chapter 2 §2.6, p. 42 Template:Wayback

[5] Template:Citation, Chapter 38 §38.2, p. 1046,1047 Template:Wayback

[6] Template:Citation, Chapter 9 §9.1, p. 261 Template:Wayback

[7] Template:Citation, Chapter 5, p. 83 Template:Wayback

[mmcm-8] 8.0 ^8.1 ^8.2 Template:Cite book

[9] H.R.Petry,B.Metsch; Theoretische Mechanik (Oldenburg, München 2005) 第18页 ISBN 3-486-24673-9

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

伽利略变换

目录

平移

三種伽利略變換

伽利略群的中心擴張

參見

備註

导航菜单

伽利略变换

平移

三種伽利略變換

伽利略群的中心擴張

參見

備註

导航菜单

搜索