外代数

Template:Copyedit Template:NoteTA

 Template:Multiple image

外代数（Template:Lang-en）也稱為格拉斯曼代数（Grassmann algebra），以紀念数学家赫爾曼·格拉斯曼。

数学上，向量空间 $V$ 的外代數是一个特定有单位的结合代数，其包含了 $V$ 为其中一个子空间。它记为 $\land (V)$ 或 $\land \cdot (V)$ . 而它的乘法，称为楔积或外积，记为 $\land$ . 楔积是结合的和雙線性的；其基本性質是它在 $V$ 上是交錯的，也就是：

v \land v = 0

，對於所有向量

v \in V

这表示

u \land v = - v \land u

，對於所有向量

u, v \in V

，以及

v_{1} \land v_{2} \land \dots \land v_{k} = 0

，當

v_{1}, \dots, v_{k} \in V

线性相关时。

值得注意的是，以上三性质只对 $V$ 中向量成立，不是对代数 $\land (V)$ 中所有向量成立。

外代数事实上是“最一般的”满足这些属性的代数。这意味着所有在外代数中成立的方程只从上述属性就可以得出。 $\land (V)$ 的这个一般性形式上可以用一个特定的泛性质表示，请参看下文。

形式为 $v_{1} \land v_{2} \land \dots \land v_{k}$ 的元素，其中 $v_{1}, \dots, v_{k}$ 在 $V$ 中，称为 $k$ -向量。所有 $k$ -向量生成的 $\land (V)$ 的子空间称为 $V$ 的 $k$ -阶外幂，记为 $\land^{k} (V)$ 。外代数可以写作每个 $k$ 阶幂的直和：

Λ (V) = ⨁_{k = 0}^{\infty} Λ^{k} V

该外积有一个重要性质，就是 $k$ -向量和 $I$ -向量的积是一个 $k + I$ -向量。这样外代数成为一个分次代数，其中分级由 $k$ 给出。这些 $k$ -向量有几何上的解释：2-向量 $u \land v$ 代表以 $u$ 和 $v$ 为边的带方向的平行四边形，而3-向量 $u \land v \land w$ 代表带方向的平行六面体，其边为 $u$ , $v$ , 和 $w$ 。

外幂的主要应用在于微分几何，其中他们用来定义微分形式。因而，微分形式有一个自然的楔积。所有这些概念由格拉斯曼提出。

定义及运算律

外代数有很多种等价的定义，下面的定义是最简洁的一个。

定义: 设 $V$ 是域 $K$ 上的一个向量空间，讓 $T^{k} (V) : = \underset{k}{\underset{⏟}{V \otimes \dots \otimes V}}$ 則定義

T (V) = ⨁_{k = 0}^{\infty} T^{k} V = K \oplus V \oplus (V \otimes V) \oplus (V \otimes V \otimes V) \oplus \dots

令 $I$ 为 $V$ 的张量代数的理想（即双边理想），该理想是由所有形如 $v \otimes v$ 的张量生成的（其中 $v \in V$ 任意），则将 $V$ 上的外代数 $Λ (V)$ 定义为商代数 $T (V) / I$ ，即

Λ (V) : = T (V) / I,

并且把 $v_{1} \otimes \dots \otimes v_{k} \in T^{k} V$ 的等价类^[1] $[v_{1} \otimes \dots \otimes v_{k}] \in T (V) / I$ 记为 $v_{1} \land \dots \land v_{k}$ ，其中 $v_{1}, \dots, v_{k} \in V$ 。设 $k = 0, 1, 2, \dots,$ 称

Λ^{k} (V) : = (T^{k} V) / I

为 $V$ 的 $k$ -阶外幂（ $k$ th exterior power of $V$ ），称 $\land^{k} (V)$ 中的元素为 $k$ -向量（ $k$ -multivector）。

注：

$\forall λ \in K$ ，当且仅当 $λ = 0$ 时才有 $λ \in I$ ，因此，可以把 $Λ^{0} (V) = K / I$ 等同于 $K$ ，并且把 $[λ] \in Λ^{0} (V)$ 记为 $λ$ ；基于类似的原因，可以把 $Λ^{1} (V) = V / I$ 等同于 $V$ ，而且把 $[v] \in Λ^{0} (V)$ 记为 $v$ 。这一点是前面所讲的能够把 $[v_{1} \otimes \dots \otimes v_{k}] \in Λ^{k} (V)$ 记为 $v_{1} \land \dots \land v_{k}$ 的特例和前提。
当 $k > 1$ 时， $k$ -向量并不仅限于形如 $v_{1} \land \dots \land v_{k}$ 的元素，例如， $v_{1} \land v_{2} + w_{1} \land w_{2}$ 也是2-向量，其中 $v_{1}, v_{2}, w_{1}, w_{2} \in V$ .
理想I中的元素并不仅限于形如v⊗v的张量，例如，
1. $\forall v \in V, \forall t \in T (V)$ , 必定有 $v \otimes v \otimes t \in I$ 和 $t \otimes v \otimes v \in I$ .
2. $\forall v, w \in V$ , 由于 $(v + w) \otimes (v + w) \in I$ 和 $v \otimes v \in I$ 以及 $w \otimes w \in I$ ，显然有 $v \otimes w + w \otimes v = (v + w) \otimes (v + w) - v \otimes v - w \otimes w \in I$ ，这就有一个推论：所有的二阶对称张量都在理想 $I$ 中。
3. 由于上面的两个结论， $\forall v, w \in V$ ，我们有 $v \otimes w \otimes v = v \otimes (w \otimes v + v \otimes w) - v \otimes v \otimes w \in I$ ，这是因为等式右边的每一项都在 $I$ 中。对张量 $t \in T (V)$ 的阶数作数学归纳法，则可以证明： $\forall v \in V$ , $\forall t \in T (V)$ ，总有 $v \otimes t \otimes v \in I$ 。
设 $k = 2, 3, \dots$ ，则 $\forall α \in Λ^{k} (V)$ ， $α$ 作为等价类含有唯一的一个完全反对称的代表元 $t \in T^{k} (V)$ ，可以把这个 $k$ -阶的完全反对称张量等同于 $α$ , 详见后面的“反对称算子和外幂”一节。在有些文献中， $k$ -向量就是以这种方式定义的。

运算律 将上面的注中的内容用 $\land$ 写出，则分别给出

(1) $\forall λ \in K, α \in Λ (V)$ , $λ \land α = α \land λ = λ α .$

证明如下：作为等价类，我们从 $α \in Λ (V) = T (V) / I$ 中任意挑选一个代表元 $t$ ，则 $t \in T (V)$ 而且 $α = [t]$ 。根据商代数的定义，

λ \land α = [λ] \land [t] = [λ \otimes t] = [λ t] = λ [t] = λ α .

类似地，可以证明 $α \land λ = λ α .$

(2) 根据注3.1中的内容，显然有 $v \land v = 0, \forall v \in V$ .

(3) 根据注3.2中的内容，对任意 $v, w \in V$ 成立着

v \land w = - w \land v .

注：即使 $K$ 的特徵为2，这个公式也是对的，只不过此时有 $- 1 = 1$ 而已。

(4) 根据商代数的定义以及张量代数的性质，运算 $\land : Λ (V) \times Λ (V) \to Λ (V)$ 满足结合律和分配律：

(α \land β) \land θ = α \land (β \land θ),

(α + β) \land θ = α \land θ + β \land θ,

α \land (β + θ) = α \land β + α \land θ,

其中 $α, β, θ \in Λ (V)$ 都是任意的。

以前两条性质为例，其证明如下：设张量 $a, b, t \in T (V)$ 分别是 $α, β, θ$ 中的代表元，即 $α = [a]$ , $β = [b]$ , $θ = [t]$ , 则

(α \land β) \land θ = ([a] \land [b]) \land [t] = [a \otimes b] \land [t] = [(a \otimes b) \otimes t] = [a \otimes (b \otimes t)] = [a] \land [b \otimes t] = [a] \land ([b] \land [t]) = α \land (β \land θ),

(α + β) \land θ = ([a] + [b]) \land [t] = [a + b] \land [t] = [(a + b) \otimes t] = [a \otimes t + b \otimes t] = [a \otimes t] + [b \otimes t] = [a] \land [t] + [b] \land [t] = α \land θ + β \land θ .

(5) 根据上面的(3)和(4)，用数学归纳法可以证明： $\forall α \in Λ^{k} (V), β \in Λ^{l} (V),$

β \land α = (- 1)^{k l} α \land β .

证明从略。

基底和维数

若 $V$ 的维数是 $n$ 而 ${e_{1}, \dots, e_{n}}$ 是 $V$ 的基，则集合

{e_{i_{1}} \land e_{i_{2}} \land \dots \land e_{i_{k}} ∣ 1 \leq i_{1} < i_{2} < \dots < i_{k} \leq n}

是 $k$ 阶外幂 $\land^{k} (V)$ 的一个基。理由如下：给定任何如下形式的楔积

v_{1} \land \dots \land v_{k}

则每个向量 $v_{j}$ 可以记为基向量 $e_{i}$ 的一个线性组合；利用楔积的双线性性质，这可以扩张为那些基向量的楔积的线性组合。任何出现同样基向量两次的楔积为0；任何基向量出现的次序不正确的可以重新排序，在交换任何两个基向量的时候变换符号。一般来讲，最后基 $k$ -向量前的系数可以用通过积 $e_{i}$ 来描述 $v_{j}$ 的矩阵的子式来计算。

数一下基元素，我们可以看到 $\land^{k} (V)$ 的维数是n 取 k。特别的有， $\land^{k} (V) = {0}$ 对于 $k > n$ .

外代数是一个分级代数，是如下直和

Λ (V) = Λ^{0} (V) \oplus Λ^{1} (V) \oplus Λ^{2} (V) \oplus \dots \oplus Λ^{n} (V)

其维数等于二项式系数之和，也就是 $2^{n}$ .

例子: 欧氏三维空间的外代数

考虑空间 $ℝ^{3}$ ，其基为 ${i, j, k}$ 。一对向量

𝐮 = u_{1} 𝐢 + u_{2} 𝐣 + u_{3} 𝐤

𝐯 = v_{1} 𝐢 + v_{2} 𝐣 + v_{3} 𝐤

的楔积为

𝐮 \land 𝐯 = (u_{1} v_{2} - u_{2} v_{1}) (𝐢 \land 𝐣) + (u_{1} v_{3} - u_{3} v_{1}) (𝐢 \land 𝐤) + (u_{2} v_{3} - u_{3} v_{2}) (𝐣 \land 𝐤)

其中 ${i \land j, i \land k, j \land k}$ 是三维空间 $\land^{2} (ℝ^{3})$ 的基底。

再加一个向量

𝐰 = w_{1} 𝐢 + w_{2} 𝐣 + w_{3} 𝐤

,

这三个向量的楔积是

𝐮 \land 𝐯 \land 𝐰 = (u_{1} v_{2} w_{3} + u_{2} v_{3} w_{1} + u_{3} v_{1} w_{2} - u_{1} v_{3} w_{2} - u_{2} v_{1} w_{3} - u_{3} v_{2} w_{1}) (𝐢 \land 𝐣 \land 𝐤)

其中 $i \land j \land k$ 是一维空间 $\land^{3} (ℝ^{3})$ 的基底。

空间 $\land^{1} (ℝ^{3})$ 是 $ℝ^{3}$ , 而空间 $\land^{0} (ℝ^{3})$ 是 $ℝ$ 。取所有四个子空间的直和得到一个向量空间 $\land (ℝ^{3})$ ，这是八维向量空间

𝐚 = (a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}, a_{8}) : = (a_{1}, a_{2} 𝐢 + a_{3} 𝐣 + a_{4} 𝐤, a_{5} 𝐢 \land 𝐣 + a_{6} 𝐢 \land 𝐤 + a_{7} 𝐣 \land 𝐤, a_{8} 𝐢 \land 𝐣 \land 𝐤)

.

那么，给定一对8维向量 $a$ 和 $b$ , 其中 $a$ 如上给出，而

𝐛 = (b_{1}, b_{2}, b_{3}, b_{4}, b_{5}, b_{6}, b_{7}, b_{8})

,

$a$ 和 $b$ 的楔积如下(用列向量表达),

𝐚 \land 𝐛 = (\begin{matrix} a_{1} b_{1} \\ a_{1} b_{2} + a_{2} b_{1} \\ a_{1} b_{3} + a_{3} b_{1} \\ a_{1} b_{4} + a_{4} b_{1} \\ a_{1} b_{5} + a_{5} b_{1} + a_{2} b_{3} - a_{3} b_{2} \\ a_{1} b_{6} + a_{6} b_{1} + a_{2} b_{4} - a_{4} b_{2} \\ a_{1} b_{7} + a_{7} b_{1} + a_{3} b_{4} - a_{4} b_{3} \\ a_{1} b_{8} + a_{8} b_{1} + a_{2} b_{7} + a_{7} b_{2} - a_{3} b_{6} - a_{6} b_{3} + a_{4} b_{5} + a_{5} b_{4} \end{matrix})

.

容易验证8维楔积以向量 $(1, 0, 0, 0, 0, 0, 0, 0)$ 为乘法幺元。也可以验证该 $\land (ℝ^{3})$ 代数的楔积是结合的(也是双线性的):

(𝐚 \land 𝐛) \land 𝐜 = 𝐚 \land (𝐛 \land 𝐜) \forall 𝐚, 𝐛, 𝐜 \in Λ (𝐑^{3}),

所以该代数是有单位且结合的。

叉乘的实质，赝向量与赝标量

对三维欧几里得空间 $E^{3}$ 可以建立一个线性同构 $ϕ : Λ^{2} (E^{3}) \to E^{3}$ 如下：任取 $E^{3}$ 的右手的标准正交基 $𝒊$ ， $𝒋$ ， $𝒌$ ，规定 $ϕ$ 把 $𝒊 \land 𝐣$ ， $𝒋 \land 𝒌$ ， $𝒌 \land 𝒊$ 分别映射为 $𝒌$ ， $𝒊$ ， $𝒋$ ，则 $ϕ$ 的定义与右手的标准正交基如何选取无关。

不难看出，对任意向量 $𝒖$ 和 $𝒗$ ，这个线性同构把 $𝒖 \land 𝒗$ 映射为 $𝒖 \times 𝒗$ 。这就是叉乘（向量积）的实质。例如， $E^{3}$ 中平行四边形 $A B C D$ 的面积向量可以表示为 $\vec{A B} \times \vec{A D}$ . 经过推广之后，高维黎曼流形 $(M, 𝐠)$ 中的紧的二维曲面 $Σ$ 的面积则可以用

\int_{Σ} \sqrt{h} d u^{1} \land d u^{2}, h = | \begin{matrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{matrix} |,

来计算（其中 $h_{a b}$ 是度规张量场 $𝐠$ 在 $Σ$ 上的诱导度规 $𝐡 = h_{a b} d u^{a} \otimes d u^{b}$ 的坐标分量），由此可以看到外积和叉乘的深刻关系。

在物理学中，向量（极向量）与赝向量（轴向量）两个概念经常需要加以区分。从根本上说，向量是 $E^{3}$ 中的元素，所以在空间反演变换下不会改变方向；而赝向量其实是 $Λ^{2} (E^{3})$ 中的元素，故在空间反演变换下会改变方向。

类似地，借助于右手的标准正交基，可以把 $Λ^{3} (E^{3})$ 中的元素 $a 𝒊 \land 𝒋 \land 𝒌$ 映射为“标量" $a \in ℝ = Λ^{0} (E^{3})$ 。但是，在空间反演变换下它就会原形毕露，所以称它为赝标量。真正的标量在空间反演下是不变的，而赝标量在空间反演下会改变符号。

把 2-向量 $𝒖 \land 𝒗$ 映射为向量 $𝒖 \times 𝒗$ 以及把 3-向量 $a 𝒊 \land 𝒋 \land 𝒌$ 映射为一个实数 $a$ 的映射实际上是一个叫做霍奇对偶的线性映射。

泛性质及构造

令 $V$ 为一个域 $K$ （在多数应用中，也就是实数域）上的向量空间。 $\land (V)$ 是“最一般”的包含 $V$ 的并有一个交替乘法在 $V$ 上由单位的结合 $K$ -代数这个事实可以用如下的泛性质形式化的表达：

任给一个有单位的结合 $K$ -代数 $A$ 和一个 $K$ -线性映射 $j : V \to A$ 使得 $j (v) j (v) = 0$ 对于每个 $v$ 属于 $V$ 成立，则存在恰好一个由单位的代数同态 $f : \land (V) \to A$ 使得 $f (v) = j (v)$ 所有 $v$ 属于 $V$ 成立。

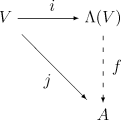
要构造最一般的包含 $V$ 的代数，而且其乘法是在 $V$ 上交替的，很自然可以从包含 $V$ 的最一般的代数开始，也就是张量代数 $T (V)$ ，然后通过合适的商来强制交替的性质。这样我们取 $T (V)$ 中由所有形为 $v \otimes v$ 的元素生成的双边理想 $I$ ，其中 $v$ 属于 $V$ ，并定义 $\land (V)$ 为商

\land (V) = T (V) / I

（并且使用 $\land$ 为 $\land (V)$ 中的乘法的代号）。然后可以直接证明 $\land (V)$ 包含 $V$ 并且满足上述泛性质。

如果不是先定义 $\land (V)$ 然后把外幂 $\land^{k} (V)$ 等同为特定的子空间，我们也可以先定义空间 $\land^{k} (V)$ 然后把它们合并成为一个代数 $\land (V)$ 。这个方法在微分集合中常常用到，并在下节中有描述。

反对称算子和外幂

给定两个向量空间 $V$ 和 $X$ ，一个从 $V^{k}$ 到 $X$ 的反对称算子是一个多线性映射

f : V^{k} \to X

使得只要 $v_{1}, \dots, v_{k}$ 是 $V$ 中线性相关的向量，则

f (v_{1}, \dots, v_{k}) = 0

.

最著名的例子是行列式值，从 $(K^{n})^{n}$ 到 $K$ 的反对称线形算子。

映射

w : V^{k} \to \land^{k} (V)

它关联 $V$ 中的 $k$ 个向量到他们的楔积，也就是它们相应的 $k$ -向量，这也是反对称的。事实上，这个映射是定义在 $V^{k}$ 上的“最一般”的反对称算子：给定任何其它反对称算子 $f : V^{k} \to X$ ，存在一个唯一的线性映射 $φ : \land^{k} (V) \to X w i t h f = φ \circ w$ 。这个泛性质表述了空间 $\land^{k} (V)$ 并且可以作为它的定义。

所有从 $V^{k}$ 到基域 $K$ 的反对称映射组成一个向量空间，因为两个这样的映射的和、或者这样一个映射和一个标量的乘积也是反对称的。若 $V$ 是有限维的，维数 $n$ ，则该空间可以认同为 $\land^{k} (V^{*})$ ，其中 $V^{*}$ 表示 $V$ 的对偶空间。特别的有，从 $V^{k}$ 到 $K$ 的反对称映射的空间是 $n$ 取 $k$ 维的。

在这个等同关系下，若基域是 $R$ 或者 $C$ ，楔积有一个具体的形式：它从两个给定的反对称映射得到一个新的反对称映射。设 $ω : V^{k} \to K$ 和 $η : V^{m} \to K$ 为两个反对称映射。和在多线性映射的张量积的情况一样，楔积的变量数是每个映射的变量数之和。它定义如下：

ω \land η = \frac{(k + m)!}{k! m!} A l t (ω \otimes η)

其中多线性映射的交替 $A l t$ 定义为其变量的所有排列的带符号平均：

A l t (ω) (x_{1}, \dots, x_{k}) = \frac{1}{k!} \sum_{σ \in S_{k}} s g n (σ) ω (x_{σ (1)}, \dots, x_{σ (k)})

注意： 有一些书中楔积定义为

ω \land η = A l t (ω \otimes η)

指标记法

在主要由物理学家使用的指标记法中有：

(ω \land η)_{a_{1} \dots a_{k + m}} = \frac{1}{k! m!} ϵ_{a_{1} \dots a_{k + m}}^{b_{1} \dots b_{k} c_{1} \dots c_{m}} ω_{b_{1} \dots b_{k}} η_{c_{1} \dots c_{m}}

微分形式

令 $M$ 为一个微分流形。一个微分k-形式 $ω$ 是 $\land^{k} T^{*} M$ （ $M$ 的余切丛的 $k$ 阶外幂）的一个截面。等价的有： $ω$ 是 $M$ 的光滑函数，对于 $M$ 的每个点 $x$ 给定一个 $\land^{k} {(T_{x} M)}^{*}$ 的元素。大致来讲，微分形式是余切向量的全局版本。微分形式是微分几何的重要工具，其中，它们被用于定义德拉姆上同调和亚历山大-斯潘尼尔上同调。

推广

给定一个交换环 $R$ 和一个 $R$ -模 $M$ ，我们可以定义和上文一样的外代数 $\land (M)$ ，它是张量代数 $T (M)$ 适当的商。它会满足类似的泛性质。

物理应用

格拉斯曼代数在物理中有重要应用，它们被用于建模和费米子和超对称性相关的各种概念。

参看：超空间，超代数，超群

注释

↑ 由下述等价关系 $\sim$ 所形成的等价类：
$\forall u, v \in T (V), u \sim v \Leftrightarrow u - v \in I .$

外代数

目录

定义及运算律

基底和维数

例子: 欧氏三维空间的外代数

叉乘的实质，赝向量与赝标量

泛性质及构造

反对称算子和外幂

指标记法

微分形式

推广

物理应用

注释

相关课题

导航菜单

外代数

定义及运算律

基底和维数

例子: 欧氏三维空间的外代数

叉乘的实质，赝向量与赝标量

泛性质及构造

反对称算子和外幂

指标记法

微分形式

推广

物理应用

注释

相关课题

导航菜单

搜索