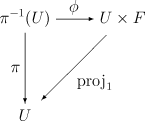纤维丛

Template:NoteTATemplate:No footnotes 纖維-{}-束（fiber bundle 或 fibre bundle）又稱纖維-{}-叢，在数学上，特别是在拓扑学中，是一个局部看来像直积空间，但是整体可能有不同的结构。每个纤维丛對應一个连续满射

$\pi :E\to B$

$E$和乘積空間$B\times F$的局部類似性可以用映射 $\pi$ 來說明。也就是說：在每個$E$的局部空間 $U$，都存在一個相同的$F$（$F$稱作纖維空間），使得 $\pi$ 限制在 $U$ 上時　與直积空间$B\times F$的投影$P:B\times F\mapsto B,P(b,f)=b$　相似。（通常會用此滿射：$\pi :E\to B$來表示一個纖維叢，而忽略$F$）

如果$E=B\times F$，也就是一个可以整体上等於乘積空間的丛叫做平凡丛（trivial bundle）。

纤维丛扩展了向量丛(vector bundle)，向量丛的主要实例就是流形的切丛（tangent bundle）。他们在微分拓扑和微分几何领域有着重要的作用。他们也是规范场论的基本概念。

正式定義

一个纤维丛由四元组（$E$, $B$, $\pi$, $F$）组成，其中$E$, $B$, $F$是拓扑空间而$\pi :E\to B$是一个连续满射，满足下面给出的局部平凡（local triviality）条件。$B$称为丛的基空间（base space），$E$称为总空间（total space），而$F$称为纤维（fiber）。映射$\pi$称为投影映射.下面我们假定基空间$B$是连通的。

我们要求对于$B$中的每个點$x$，存在一个在$B$中 包含$x$的开邻域$U$，並有一個同胚映射$\phi :{\pi }^{-1}(U)\to U\times F$ (顯然$U\times F$是一個乘積空間) ，$\phi$並且要滿足 $\pi (y)={\mathrm{proj}}_1\circ \varphi (y),\mathrm{\forall }y\in {\pi }^{-1}(U)$，也就是下圖是可交换的：

其中${\mathrm{proj}}_1:U\times F\to U$是自然投影而$\phi :{\pi }^{-1}(U)\to U\times F$是一个同胚（這裡的局部平凡條件有些書會定義為 $x=\pi \circ {\phi }^{-1}(x,f),\mathrm{\forall }x\in U,f\in F$）。所有$\{(U_i,{\phi }_i)\}$的集合称为丛的局部平凡化。

对于$B$中每點$p$，原象（preimage）${\pi }^{-1}(p)$和$F$同胚并称为點$p$上的纤维。一个纤维丛（$E$, $B$, $\pi$, $F$）经常记为

$F⟶E\stackrel{\pi }{\to }B$

以引入一个空间的短恰当序列。注意每个纖維叢$\pi :E\to B$都是一个开映射，因为积空间的投影是开映射。所以$B$有由映射$\pi$决定的商拓扑(quotient topology).

一个光滑纤维丛是一个在光滑流形的范畴内的纤维丛。也就是，$E$, $B$, $F$都必须是光滑流形且所有上面用到的函数都必须是光滑映射。

例子

令$E=B\times F$并令$\pi :E\to B$为对第一个因子的投影，则$E$是$B$上的丛。这里$E$不仅是局部的积而且是整体的积。任何这样的纤维丛称为平凡丛。

莫比乌斯带是圆上的非平凡丛。

最简单的非平凡丛的例子可能要算莫比乌斯带（Möbius strip）。莫比乌斯带是一个以圆为基空间$B$并以线段为纤维$F$的丛。对于一点$x\in B$的邻域是一段圆弧；在图中，就是其中一个方块的长。原象${\pi }^{-1}(U)$在图中是个（有些扭转的）切片，4个方块宽一个方块长。同胚$\phi$把$U$的原象映到柱面的一块：弯曲但不扭转。

相应的平凡丛$B\times F$看起来像一个圆柱，但是莫比乌斯带有个整体上的扭转。注意这个扭转只有整体上才能看出来；局部看来莫比乌斯带和圆柱完全一样（在其中任何一个竖直的切一刀会产生同样的空间）。

一个类似的非平凡丛是克莱因瓶，它可以看作是一个“扭转”的圆在另一个圆上的丛。相应的平凡丛是一个环，$S^1\times S^1$。

一个覆盖空间是一个以离散空间为纤维的纤维丛。

纤维丛的一个特例，叫做向量丛,是那些纤维为向量空间的丛（要成为一个向量丛，丛的结构群—见下面—必须是一个线性群）。向量丛的重要实例包括光滑流形的切丛和余切丛。

另一个纤维丛的特例叫做主丛。更多的例子参看该条目。

一个球丛是一个纤维为n維球面的纤维丛。给定一个有度量的向量丛（例如黎曼流形的切丛），可以构造一个相应的单位球丛，其在一点$x$的纤维是所有$E_x$的单位向量的集合.

截面

Template:Main 纤维丛的截面（section或者cross section）是一个连续映射$f:B\to E$使得$\pi (f(x))=x$对于所有$B$中的$x$成立。因为丛通常没有全局有定义的截面，理论的一个重要作用就是检验和证明他们的存在性。这导致了代数拓扑的示性类理论。

截面经常只被局部的定义（特别是当全局截面不存在时）。纤维丛的局部截面是一个连续映射$f:U\to E$其中$U$是一个$B$中的开集而$\pi (f(x))=x$对所有$U$中的$x$成立。若$(U,\phi )$是一个局部平凡化图，则局部截面在$U$上总是存在的。这种截面和连续映射$U\to F$有1-1对应。截面的集合组成一个层（sheaf）。

结构群和转移函数

纤维丛经常有一个对称群描述重叠的图之间的相容条件。特别的，令$G$为一个拓扑群，它连续的从左边作用在纤维空间$F$上。不失一般性的，我们可以要求$G$有效的作用在$F$上，以便把它看成是$F$的同胚群。纖維叢的一个$G$-图册（$E$, $B$, $\pi$, $F$）是之前定義過的局部平凡化並且滿足：对任何两个重叠的局部平凡化中的元素也就是图$(U_i,{\phi }_i)$和$(U_j,{\phi }_j)$且 $U_i\cap U_j\ne \mathrm{\varnothing }$，則函数

${\phi }_i{\phi }_j^{-1}:(U_i\cap U_j)\times F\to (U_i\cap U_j)\times F$

是由以下方式给出：

${\phi }_i{\phi }_j^{-1}(x,\xi )=(x,t_{ij}(x)\xi ),\mathrm{\forall }x\in U_i\cap U_j,\xi \in F$

其中 $t_{ij}:U_i\cap U_j\to G$ 是一个称为转移函数（transition function）的连续映射。两个$G$-圖冊是等價的如果他们的聯集也是$G$-圖冊。一个$G$-丛是有$G$-圖冊等价类的纤维丛。群$G$稱为该丛的结构群（structure group）。

在光滑范畴中，一个$G$-丛是一个光滑纤维丛，其中$G$是一个李群而相应的在$F$上的作用是光滑的并且变换函数都是光滑映射。

转移函数$t_{ij}$满足以下条件

1. $t_{ii}(x)=1$
2. $t_{ij}(x)=t_{ji}(x{)}^{-1}$
3. $t_{ik}(x)=t_{ij}(x)t_{jk}(x)$

第三个条件用到三個相交的 $U_i\cap U_j\cap U_k$上叫做上链条件（cocycle condition，见Čech上同调）。

一个主丛是一个$G$-丛，其纤维可以认为是$G$本身，并且有一个在全空间上的$G$的右作用保持纤维不变。

参见

• 向量丛
• 主丛
• 拉回丛（pullback bundle）
• 纤维化
• 覆盖映射
• 规范场论

外部链接

• PlanetMath: Fiber Bundle
• MathWorld: Fiber Bundle Template:Wayback

参考

• Norman Steenrod, The Topology of Fiber Bundles, Princeton University Press (1951). ISBN 0-691-00548-6.
• David Bleecker, Gauge Theory and Variational Principles, Addison-Wesley publishing, Reading, Mass (1981). ISBN 0-201-10096-7. See chapter one.