小星形十二面體

来自testwiki
跳转到导航 跳转到搜索

Template:NoteTA Template:Infobox polyhedron 小星形十二面體是一種星形正多面體，由12個五角星面組成，為三種星形十二面體之一。[1][2]小星形十二面體的凸包為正二十面體，而正二十面體的對偶多面體為正十二面體，因此小星形十二面體的對偶多面體也是一種星形十二面體——大十二面體；[3]Template:Rp此外，其頂點的布局與正二十面體相同，但邊的連結方式不同，因此可以視為正二十面體經過Template:Link-en後的多面體。[4]小星形十二面體的拓樸結構與大十二面體相同，皆對應到虧格為4的五階五邊形正則地區圖（施萊夫利符號：{5,5}），[5]因此小星形十二面體和大十二面體皆可以視為抽象多面體{5,5}6[註 1]在三維空間中的一種具象化形式。[6]這個多面體最早由约翰内斯·开普勒於1619年觀察並描述，[7]並於1809年由Template:Link-en重新發現；[8]1859年阿瑟·凱萊對這種形狀進行進一步的研究並將之命名為小星形十二面體（Small stellated dodecahedron）。[9]

有些藝術家會利用小星形十二面體的星狀外形作為表達天體意象的方式，例如在艾雪的作品《Template:Le》中就使用了小星形十二面體作為創作中的主要元素。[10][11]

歷史

小星形十二面體的形狀最早出現於保羅·烏切洛在1430年創作於威尼斯聖馬爾谷聖殿宗主教座堂地板上的鑲嵌藝術中，然而當時尚未對這種形狀的性質進行探討，僅作為藝術作品的要素之一。[12]1619年，约翰内斯·开普勒在其著作《世界的和諧》中針對部分星形多面體進行了一些研究，[13]當中包括了大星形十二面體與小星形十二面體。[7]1809年Template:Link-en重新發現了开普勒先前發現的星形多面體並另外發現了兩個星形多面體：大二十面體與大十二面體，因此這四個立體現今合稱為克卜勒－龐索立體。[8]1859年，阿瑟·凱萊對這種形狀進行了較詳細的描述，並將其命名為小星形十二面體（Template:Lang），[9]同時這也是這種立體首次在正式文獻中獲命名。[7]然而，由於這個立體由12個面、30條邊和12個頂點組成，而這些數值代入當時認為能普遍適用於各種多面體的欧拉示性数得到了不是2的結果，與當時普遍的認知相左，因此這種幾何結構一度被認為不應存在。[14]這個問題後來在克萊茵的著作中得到了解答，[15]這個立體代表著一個虧格為4的黎曼曲面。[16]

性質

小星形十二面體由組成12個面、30條邊和12個頂點組成，[17]其中，12個面皆為正五角星；在組成小星形十二面體的12個頂點中，每個頂點都是5個五角星的公共頂點，在頂點圖中，可使用五邊形來表示；[18][4]每條邊皆等長，且皆為2個正五角星的公共邊。由此可知，這個立體具備了所有面全等、所有邊等長、所有角等角的性質，是一種正多面體，然而這種立體是一個非凸多面體，因此不在古典的5種多面體中，是4個非凸正多面體之一，[8]由12個五角星面（6對平行五角星）所組成。小星形十二面體在施萊夫利符號中利用{5/2,5}來表示，這個符號代表了每個頂點都是5個五角星的公共頂點，在Template:Link-en中利用Template:CDD來表示。[19]

構造

小星形十二面體是一種星形十二面體，其可透過延伸正十二面體的面來構成，[4]這個操作就有如將正五邊形的邊延伸至相交，構成正五角星；同理，小星形十二面體則為將正十二面體以正五邊形延伸成正五角星的方式，將面延伸至相交。這個操作將在正十二面體的每個面上加入一個五角錐，錐高為15(5+25)。[19]

二面角

小星形十二面體是一種星形正多面體，因此具有所有角相等的性質。其二面角只有一个值，其值為負五平方根倒數之反餘弦：[17]

cos−1(−55)≈2.03444394≈116.565051177∘

面的組成

小星形十二面體由12個五角星面組成，這些五角星皆全等，並且其構成方式為由正五邊形的頂點，以間隔為2的方式相接，在施萊夫利符號中可以用{5/2}來表示，[20]而小星形十二面體每個頂點都是5個五角星面的公共頂點，在施萊夫利符號中表示為{5/2,5}。在拓樸學上，這種結構與{5,5}無異，因此小星形十二面體也可以視為將五階五邊形鑲嵌這種雙曲鑲嵌局部區域閉合後的結果。[20]


以黃色表示小星形十二面體的五角星面
小星形十二面體
將一個面以藍色表示，其他面不著色

此外，亦可以將小星形十二面體化為簡單多面體，即排除面與面自相交的情況。通常用於製作小星形十二面體的模型，因為自相交的面不容易用實體模型實現，此時會將小星形十二面體的12個五角星面分割成60個等腰三角形面。[21]

拓樸

若將小星形十二面體的五角星依照複雜多邊形的方式[註 2]分解成5個等腰三角形，則其拓樸結構將與五角化十二面體等價，只是前者的錐高更高，而使其成為非凸多面體；[19]若將五角化十二面體的原像——正十二面體視為一個截對角偏方面體，則對應的小星形十二面體則為該5個側面所加入的5個角錐中，5個側面共面成五角星。另一方面，若使小星形十二面體的五角星維持原樣，則其拓樸結構與大十二面體相同，並對應相同的正則地區圖，[24]對應的骨架圖為二十面體圖。[25][24]

小星形十二面體由12個五角星、30條邊和12個頂點組成，可以透過歐拉公式計算其虧格：

V−E+F=2−2g

由此可知，小星形十二面體代表了一個虧格為4的曲面。這個特性最初被Template:Link-en觀察到時，十分令人困惑，[15]而费利克斯·克莱因在1877年表明，小星狀十二面體可以被視為虧格為4之黎曼曲面被黎曼球面Template:Link-en的結果，其分支點位於每個五角星的中央。[16]而這個黎曼曲面稱為Template:Link-en，其對稱性是所有虧格為4之黎曼曲面中最多的，對應自同構群為S5對稱群。[26]

使用

不少藝術家有使用小星形十二面體進行創作，例如保羅·烏切洛在1430年創作於威尼斯聖馬爾谷聖殿宗主教座堂地板上的鑲嵌藝術中就能發現小星形十二面體的蹤影；[12]相同的形狀也出現在兩件莫里茨·科内利斯·埃舍尔的兩件石版印刷作品中，分別是1950年創作的《Contrast》與1952年創作的Template:Le。[10]

相關多面體與鑲嵌

部分多面體與鑲嵌與小星形十二面體有一些幾何關聯。例如部分多面體可透過小星形十二面體經過康威變換而得到，例如截角大十二面體、截半大十二面體[27]、以及其對偶多面體大十二面體[19]。

關聯 原像 對偶多面體 皮特里對偶
名稱 小星形十二面體 大十二面體 皮特里小星形十二面體
施萊夫利符號 {5/2,5} {5,5/2} {5/2,5}Template:Pi
圖像

截角小星形十二面體

Template:Main

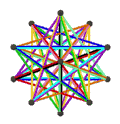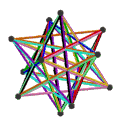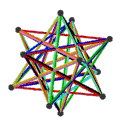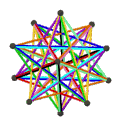
不同截角深度的截角小星形十二面體

截去所有頂點的小星形十二面體[註 3][31]可構成一個外觀與正十二面體無異的退化均勻多面體。[32][33]這種多面體在考克斯特記號中可以用Template:CDD表示。[34]雖然其外觀與正十二面體無異，然而這種立體並非十二面體，而是一種退化的二十四面體，其由24個面、90條邊和60個頂點組成，其中24個面為12個正五邊形和12個繞兩圈的正五邊形組成，整體可以視為是每個頂點都是2個十邊形和1個五邊形之公共頂點的抽象等角二十四面體的具像化。[35]

不同的截角深度也會產生不同的幾何體：

名稱 小星形十二面體 截角小星形十二面體 截半大十二面體 截角大十二面體 大十二面體
Template:Link-en Template:CDD Template:CDD Template:CDD Template:CDD Template:CDD
圖像

簡單多面體

幾種可基於正十二面體構造而得的立體

小星形十二面體可以化為簡單多面體，此時會將小星形十二面體的12個五角星面分割成60個等腰三角形面，[21]此時其拓樸結構將與五角化十二面體等價，[19]由60個面、90條邊和32個頂點組成。[36]這種立體可以三角化成其他立體：

大二十面體 向內加入角錐 （原始形狀） 向外加入角錐 完全星形二十面體

貝齊奧立體

Template:See also 讓-伊夫·貝齊奧曾在其論文中探討星形十二面體，[37]但不慎將以五邊形組成的正十二面體之星形化體與菱形組成的菱形十二面體之星形化體搞混了。後來莫雷帝將其描述為在正十二面體的面上加入五角錐組成的立體，[38]即小星形十二面體。 後來，漢士·史梅斯特（Hans Smessaert）等人才以星形四角化菱形十二面體的結構完成貝齊奧最初探討的議題。[39]


莫雷帝描述的貝齊奧立體
（實為小星形十二面體）
漢士·史梅斯特描述的貝齊奧立體

星形鑲嵌圖

其也可以視為一系列施萊夫利符號中可利用{n/2,n}表示的星形鑲嵌之一，例如七階七角星鑲嵌：[40][41] Template:星形多面體和鑲嵌系列

對偶複合體

Template:Main

小星形十二面體與其對偶多面體的複合體為複合小星形十二面體大十二面體。其共有24個面、60條邊和24個頂點，其尤拉示性數為-12，虧格為7，[42]而在這個立體圖形中，僅有小星形十二面體可見，大十二面體完全隱沒於小星形十二面體而不可見。[43]

參見

Template:Commons category

註釋

  1. ↑ {5,5}6為施萊夫利符號，其代表了每個頂點都是5個五邊形的公共頂點，並具有六邊形的皮特里多邊形。
  2. ↑ 在複雜多邊形中，自相交偶數次的部份算做多邊形的外部，[22]以此例而言，五角星中央交出的五邊形不算做五角星的內部，換句話說，即是此複雜多邊形的孔洞。[23]
  3. ↑ 產生半正多面體所用的截角，即確保截角完後的面皆要等邊的截角。[29][30]

参考文献

Template:Reflist

Template:星形正多面体 Template:廣義的正多面體 Template:Authority control Template:Good article

  1. ↑ Template:Cite mathworld
  2. ↑ Template:Cite book
  3. ↑ Template:Citation
  4. ↑ 4.0 4.1 4.2 Template:Cite web
  5. ↑ Template:Cite web
  6. ↑ Template:Cite web
  7. ↑ 7.0 7.1 7.2 Template:Cite MathWorld
  8. ↑ 8.0 8.1 8.2 Louis Poinsot, Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9, pp. 16–48, 1810.
  9. ↑ 9.0 9.1 Template:Cite journal
  10. ↑ 10.0 10.1 Template:Cite book
  11. ↑ Locher, J. L. (2000). The Magic of M. C. Escher. Harry N. Abrams, Inc. Template:ISBN
  12. ↑ 12.0 12.1 Template:Cite book See in particular p. 42.
  13. ↑ Template:Cite book
  14. ↑ Template:Cite journal
  15. ↑ 15.0 15.1 Template:Cite journal
  16. ↑ 16.0 16.1 Template:Citation
  17. ↑ 17.0 17.1 Template:Cite web
  18. ↑ Template:Cite web
  19. ↑ 19.0 19.1 19.2 19.3 19.4 Template:Cite MathWorld
  20. ↑ 20.0 20.1 Template:Cite journal
  21. ↑ 21.0 21.1 Template:Cite web
  22. ↑ Template:Cite web
  23. ↑ Rae Earnshaw, Brian Wyvill (Ed); New Advances in Computer Graphics: Proceedings of CG International ’89, Springer, 2012, page 654.
  24. ↑ 24.0 24.1 Template:Cite web
  25. ↑ Template:Cite wolframalpha
  26. ↑ Template:Cite journal pdf Template:Wayback
  27. ↑ Template:Cite book
  28. ↑ Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. Template:Isbn
  29. ↑ Coxeter, H.S.M. Chapter 8: Truncation, Regular Polytopes,[28] pp. 145–154
  30. ↑ Norman Johnson, Uniform Polytopes, Manuscript (1991)
  31. ↑ Template:GlossaryForHyperspace
  32. ↑ Template:Cite web
  33. ↑ Template:Cite journal
  34. ↑ Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
  35. ↑ Template:Cite journal
  36. ↑ Template:Cite web
  37. ↑ Template:Cite journal
  38. ↑ Template:Cite journal
  39. ↑ Template:Citation
  40. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, Template:Isbn (Chapter 19, The Hyperbolic Archimedean Tessellations)
  41. ↑ Template:Cite book
  42. ↑ Template:Cite web
  43. ↑ Template:Cite mathworld
检索自“https://zh.wiki.beta.math.wmflabs.org/w/index.php?title=小星形十二面體&oldid=3046”