零假设
跳转到导航
跳转到搜索
Template:Expand language Template:NoteTA
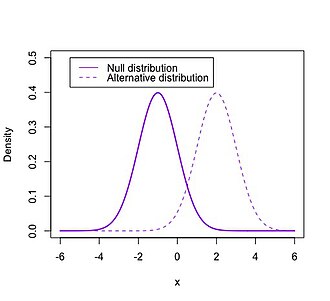
在推論統計學中,零假设(Template:Lang-en,又译-{zh-cn:虚无假设、原假设; zh-tw:零假說;}-,符号:)是做统计检验时的一类假說。
零假设的内容一般是希望能证明为错误的假设,与零假设相对的是對立假說,即希望通过证伪零假设而证明正确的另一种假说。从数学上来看,零假设和备择假设的地位是相等的,但是在统计学的实际运用中,常常需要强调一类假设为应当或期望实现的假设,例如在相关性检验中,一般会取“两者之间无关联”作为零假设,而在独立性检验中,一般会取“两者之间非獨立”作为零假设。
如果一个统计检验的结果拒绝(reject)零假设(结论不支持零假设),而实际上真实的情况属于零假设,那么称这个检验犯了型一錯誤。反之,如果检验结果支持零假设,而实际上真实的情况属于备择假设,那么称这个检验犯了型二錯誤。通常的做法是,在保持第一类错误出现的机会在某个特定水平上的时候(即显著性差异值或α值),尽量减少第二类错误出现的概率。
相关条目
参考来源
延伸閱讀
- Template:Cite book
- Template:Cite journal The application of significance testing in this paper is an outlier. Tests to find a null hypothesis? Not trying to show significance, but to find interesting cases?
- Template:Cite journal Directed tests combine the attributes of one-tailed and two-tailed tests. "...directed tests should be used in virtually all applications where one-sided tests have previously been used, excepting those cases where the data can only deviate from H0, in one direction."