辫群

辮群（Template:Lang-en）為數學領域中紐結理論的一個概念。一個 $n$ 股的辮群（記為 $B_{n}$ ）是元素為 n-braid 的群，其運算為前一個 n-braid 按後一個 n-braid 的方式操作（見 Template:Section link）。

而辮群是由埃米爾·阿廷(1925^[1])提出的，因此又被稱為阿廷辮群（Template:Lang-en）。^[2]

引言

想像有4條橫著擺放的繩子，它們的兩端分別被固定在左右兩側的牆上，如下圖所示，黑點代表被固定的位置。

我們稱這樣繩子的擺放方式，或是編織的方式為一個辮子（Template:Lang-en）。而正式的寫法中會連繩子的數目也一起表達，將4股的辮子以英文簡寫成 4-braid。

如果將剛才的辮子中下面兩條的右端交換位置，會變成下圖的樣子。

那麼這兩種會是不同的4股辮子( Template:Lang-en)。如果將這兩種辮子理解為群中的元素，那麼剛才把右端交換位置的操作就是群當中的運算。在辮群的討論中，常用這些操作來表示不同的辮子，這種表示方法稱作 braid word。^[2]

在這個小節中，以 $n = 4$ 為例。

下面的两条辫子是不同的：

不同于

但是下面的两条辫子是相同的：

同于

所有的股都必须从左向右移动，所以下面的图片并不是一条辫子：

不是辫子

我们可以编两条辫子：

加

等于

另一个例子：

加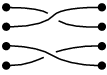

等于

复合 / 编织物σ和τ的组成写为στ。

$B_{4}$ 是四股上所有编织物的集合。上面的复合是群操作，单位元是四股水平平行股的辫子，辫子B的逆元素是取消B的操作。

辮群的應用包括陳-西蒙斯理論、亚历山大定理（Alexander's Theorem）、楊-巴克斯特方程、代数几何、任意子、等。^[3]