簡諧運動

Template:NoteTA 简谐运动，或稱简谐振动、谐振、SHM（Simple Harmonic Motion），即是最基本也是最简单的一种机械振动。当某物体进行简谐运动时，物体所受的力（或物体的加速度）的大小与位移的大小成正比，并且力（或物体的加速度）总是指向平衡位置。

如果用$F$表示物体受到的回復力，用$x$表示物体对于平衡位置的位移，根据胡克定律，$F$和$x$成正比，它们之间的关系可用下式来表示：

$F=-kx$

式中的$k$是回复力与位移成正比的比例系数；负号的意思是：回复力的方向总跟物体位移的方向相反。

根据牛顿第二定律「$F=ma$」当物体质量一定时，运动物体的加速度总跟物体所受合力的大小成正比，跟合力的方向相同，且系統的機械能守恆。

动力学方程

同一简谐运动在实空间和相空间的不同显示。Template:Le是周期性的。（为使两图一致，这里的速度轴和位置轴与标准惯例相反）

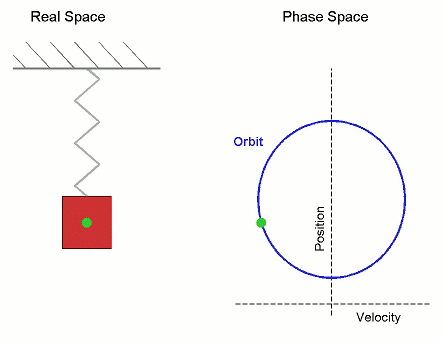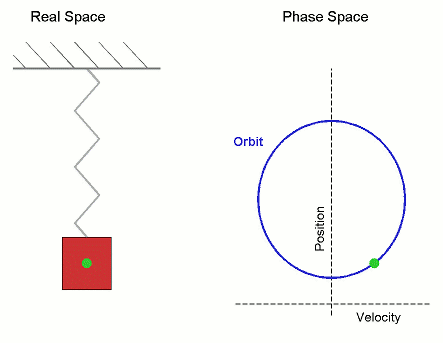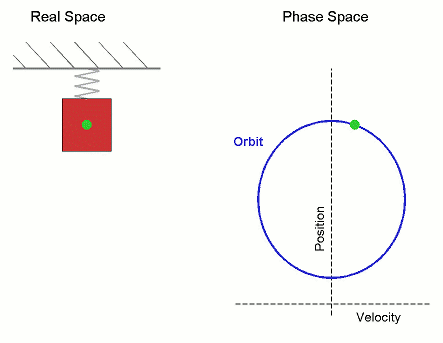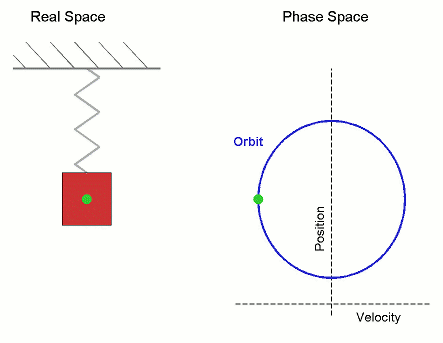
对于一维的简谐振动，其动力学方程是二阶微分方程，可由牛顿第二运动定律得到

$F=ma=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=m\ddot{x}$

回复力又可表示为$F=-kx$

所以有$\ddot{x}+\frac{k}{m}x=0$

求解上述方程，得到的解含有正弦函数

$x(t)=c_1\cos \left(\omega t\right)+c_2\sin \left(\omega t\right)=A\cos (\omega t-\phi )$，其中

$\omega =\sqrt{\frac{k}{m}},$

$A=\sqrt{{c_1}^2+{c_2}^2},$

$\tan \phi =\left(\frac{c_2}{c_1}\right),$

$c_1$，$c_2$是由初始条件决定的常数。取平衡位置为原点，每项都有物理意义：$A$是振幅，$\omega =2\pi f$是角频率， 加速度可以作为时间的函数得到

$v(t)=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega \sin (\omega t-\phi )$

$v_{max}=\omega A$（在平衡位置）

$a(t)=\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-A{\omega }^2\cos (\omega t-\phi )$

$a_{max}={\omega }^{2}A$（在最大位移处）

加速度也可以通过位移的函数得到

$a(x)=-{\omega }^{2}x$。

因为 $\omega =2\pi f$，

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$，

又因为周期 $T=\frac{1}{f}$，所以：$T=2\pi \sqrt{\frac{m}{k}}$。

以上方程说明了简谐振动具有等时性，即一个做简谐振动的质点运动周期和振幅以及相位无关。Template:Rp

线性回复力

在运动过程中，物体所受力的大小与它的位移的大小成正比，而力的方向与位移的方向相反。具有这种性质的力称为线性回复力。

彈簧

将一个有孔小球体与一个弹簧连在一在运动过程中，物体所受力的大小与它的位移的大小成正比，而力的方向与位移的方向相反。具有这种性质的力称为线性回复力。平杆穿入小球体，使球体可以在水平杆上左右滑动，而球体与水平杆的摩擦力小得可以忽略不计。将弹簧的一端固定住，弹簧的整体质量要比球体质量小得多，这样弹簧本身质量也可以忽略不计。这个系统便是一个弹簧振子。

弹簧振子系统在平衡状态下，弹簧没有形变，振子（小球体）在平衡位置保持静止。若把振子拉过平衡位置，到达最大幅度，再松开，弹簧则会将振子向平衡位置收回。在收回的过程中，弹簧的势能转换为振子的动能，势能在降低的同时，动能在增加。当振子到达平衡位置时，振子所积累的动能又迫使振子越过平衡位置，继续向同样的方向移动。但因已越过弹簧振子系统的平衡位置，所以这时弹簧开始对振子向相反方向施加力。动能转作势能，动能降低，势能上升，直至到达离平衡位置最大幅度的距离。这时振子所有的动能被转化为势能，振子速度为零，停止运动。势能又迫使振子移回平衡位置，在移动过程中，势能转为动能，因而再次越过平衡位置，重复这个过程。在没有任何其他力影响的完美的条件下，这个弹簧振子系统会在两个最大幅度点间不停地做往返运动。彈簧振子的固有週期和固有頻率與彈簧彈力係數和振子質量有關，與振幅大小無關。

振幅、週期和频率

1.振幅

振幅$A$代表质点偏离中心（平衡位置）的最大距离，它正比于$\sqrt{E}$，即它的平方正比于系统的机械能E。

2.角频率

角频率：$\omega =2\pi f$, 频率f为周期T的倒数。

其中$\omega =\sqrt{\frac{k}{m}}$。推导过程：

$x=A\cos (\omega t+\varphi )$

对于时间t求导， $v=-A\omega \sin (\omega t+\varphi )$

再关于时间t求导，$a=-A{\omega }^2\cos (\omega t+\varphi )$

由牛顿第二定律得$a=\frac{F}{m}=\frac{-kx}{m}=\frac{-A\cos (\omega t+\varphi )k}{m}$

两式联立得$\omega =\sqrt{\frac{k}{m}}$。

下图為簡諧運動的圖像，表示的是振動物體的位移隨時間變化的規律。是一條正弦或餘弦曲綫。

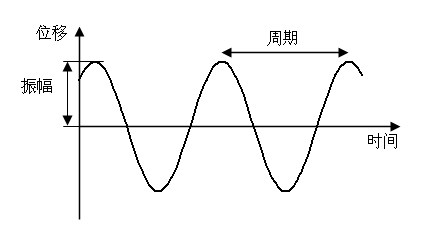
這個運動是假設在沒有能量損失引致阻尼的情況而發生。振幅描繪了振動的強弱，是標量，大小為最大位移的大小，質點在一次全振動過程中通過的路程等於4倍振幅。完成一次全振動的时间叫週期，單位時間內完成全振動的次数叫頻率，週期和頻率描繪了振動的快慢。

简谐振动的判定

应该说明：

1. 以上各判定方法是完全等价的；
2. 以上各表达式中的$x$既可以是线量（线位移），又可以是角量（角位移），相应的，速度可以为线速度和角速度，对应的加速度是线加速度和角加速度。

例子

弹簧

把质量为$M$的物体悬挂在彈力常數为k的弹簧的底端，则物体将进行简谐运动，其方程为：

$\omega =2\pi f=\sqrt{\frac{k}{M}}.$

如果要计算它的周期，可以用以下的公式：

$T=\frac{1}{f}=2\pi \sqrt{\frac{M}{k}}$。

总能量是常数，由方程$E=\frac{k{A}^2}{2}$给出。

等速率圆周運動

等速率圆周運動的一维投影是簡諧運動。如果物體以$\omega$的角速率沿着半徑为$R$的圆移動，则它在x軸、y軸或任意一條直徑上的投影會是簡諧運動，其振幅为$R$，角速率为$\omega$。

单摆

在偏角不太大的情况（一般認為小於5°）下，单摆的运动可以近似地视为简谐运动。如果单摆的长度为$\ell$，重力加速度为$g$，则周期为：

$T=2\pi \sqrt{\frac{\ell }{g}}$

这个公式仅当偏角很小时才成立，因为角加速度的表达式是与位置的正弦成正比的：

$\ell mg\sin (\theta )=I\alpha$

其中I是转动惯量，在这种情况下$I=m{\ell }^2$。当$\theta$很小时，$\sin (\theta )\approx \theta$，因此上式变为：

$\ell mg\theta =I\alpha$

这使得角加速度与$\theta$成正比，满足了简谐运动的定义。單擺的回復力是擺球的重力沿運動方向的分力。Template:Rp

参阅

• 平移运动
• 匀速运动
• 平抛运动
• 曲线运动

外部链接

• 弹簧震动Java模拟 Template:Wayback