率失真理论

数据率失真理论（Rate distortion theory）或稱信息率-失真理論（information rate-distortion theory）是信息论的主要分支，其的基本问题可以归结如下：对于一个给定的信源（source, input signal）分布与失真度量，在特定的码率下能达到的最小期望失真；或者为了满足一定的失真限制，可允許的最大码率為何，D 定義為失真的符號。

要完全避免失真幾乎不可能。處理信號時必須允許有限度的失真﹐可減小所必需的信息率。1959年﹐Claude Shannon 首先發表《逼真度準則下的離散信源編碼定理》一文，提出了率失真函數的概念。

失真函數

失真函數能量化輸入與輸出的差異，以便進行數學分析。令輸入信號為$\chi$，輸出信號為$\hat{\chi }$，定義失真函數為$d(\chi ,\hat{\chi })$，失真函數可以有多種定義，其與對應域為非負實數：

$d:\chi \times \hat{\chi }\to R_{+}$。

漢明失真

漢明失真函數能描述錯誤率，定義為：

$d(x,\hat{x})=\{\begin{array}{cc}0,& \text{if }x=\hat{x}\\ 1,& \text{if }x\ne \hat{x}\end{array}$，

對漢明失真函數取期望值即為傳輸錯誤率。

平方誤差失真

最常用於量測連續字符傳輸的失真，定義為：

$d(x,\hat{x})=(x-\hat{x}{)}^2$，

平方誤差失真函數不適用於語音或影像方面，因為人類感官對於語音或影像的平方誤差失真並不敏感。

率失真函數

下列是率與失真（rate and distortion）的最小化關係函數:

$\underset{Q_{Y|X}(y|x)}{\inf }{I}_Q(Y;X)\text{subject to}{D}_Q\le D^{*}.$

這裡 Q_{Y | X}(y | x), 有時被稱為一個測試頻道 （test channel）, 係一種條件機率之機率密度函數 (PDF)，其中頻道輸出 (compressed signal) Y 相對於來源 (original signal) X, 以及 I_Q(Y ; X) 是一種互信息（Mutual Information），在 Y 與 X 之間被定義為

$I(Y;X)=H(Y)-H(Y|X)$

此處的 H(Y) 與 H(Y | X) 是指信宿（output signal） Y 的熵（entropy）以及基於信源（source signal）和信宿（output signal）相關的條件熵（conditional entropy）, 分別為:

$H(Y)=-\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{P}_Y(y){\log }_2(P_Y(y))dy$

$H(Y|X)=-\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{Q}_{Y|X}(y|x)P_X(x){\log }_2(Q_{Y|X}(y|x))dxdy.$

這一樣來便可推導出率失真的公式, 相關表示如下:

$\underset{Q_{Y|X}(y|x)}{\inf }E[D_Q[X,Y]]\text{subject to}{I}_Q(Y;X)\le R.$

這兩個公式之間互為可逆推。

無記憶（獨立）高斯訊號來源

如果我們假設 P_X(x) 服从正态分布且方差为σ², 並且假設 X 是連續时间独立訊號（或等同於來源無記憶或訊號不相關），我們可以發現下列的率失真公式的「公式解」（analytical expression）:

$R(D)=\{\begin{array}{cc}\frac{1}{2}{\log }_2({\sigma }_x^2/D),& \text{if }0\le D\le {\sigma }_x^2\\ \\ 0,& \text{if }D>{\sigma }_x^2.\end{array}$

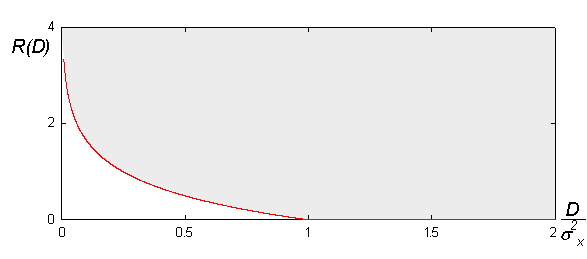
下圖是本公式的幾何面貌:

率失真理論告訴我們“沒有壓縮系統存在於灰色區塊之外”。可以說越是接近紅色邊界，執行效率越好。一般而言，想要接近邊界就必須透過增加碼塊（coding block）的長度參數。然而，塊長度（blocklengths）的取得則來自率失真公式的量化（quantizers）有關。

這樣的率失真理論（rate–distortion function）僅適用於高斯無記憶信源（Gaussian memoryless sources）。

二元信號源

伯努利信號源$X$，$X\sim Bernoulli(p)$，以漢明失真描述的率失真函數為：

$R(D)=\{\begin{array}{cc}H(p)-H(D),& 0\le D\le min\{p,1-p\}\\ 0,& D\ge min\{p,1-p\}\end{array}$

平行高斯信號源

平行高斯信號源的率失真函數為一經典的反注水算法(Reverse water-filling algorithm)，我們可以找出一閾值$\lambda$，只有方差大於$\lambda$的信號源才有必要配置位元來描述，其他信號源則可直接傳送與接收，不會超過最大可容許的失真範圍。

我們可以使用平方誤差失真函數，計算平行高斯信號源的率失真函數。注意，此處信號源不一定同分佈：

$X_1,X_2...,X_m$且$X_i\sim N(0,{\sigma }_i^2)$，此時率失真函數為，

$R(D)=\sum _{i=1}^m\frac{1}{2}log\frac{{\sigma }_i^2}{D_i}$

其中，

$D_i=\{\begin{array}{cc}\lambda ,& \text{if }\lambda <{\sigma }_i^2\\ {\sigma }_i^2,& \text{if }\lambda \ge {\sigma }_i^2\end{array}$

且$\lambda$必須滿足限制：

$\sum _{i=1}^m{D}_i=D$。