派克变换

Template:NoteTA 派克变换（也译作帕克变换，英语：Park's Transformation），是目前分析同步电动机及感應馬達运行最常用的一种坐标变换，由美国工程师Template:Le在1929年提出。派克变换将定子的a,b,c三相电流投影到随着转子旋转的直轴（d轴），交轴（q轴）与垂直于dq平面的零轴（0轴）上去，从而实现了对定子电感矩阵的对角化，对电动机的运行分析起到了简化作用。

定义

派克正变换：

𝐢_{d q 0} = 𝐏 𝐢_{a b c} = \frac{2}{3} [\begin{matrix} \cos θ & \cos (θ - 12 0^{\circ}) & \cos (θ + 12 0^{\circ}) \\ - \sin θ & - \sin (θ - 12 0^{\circ}) & - \sin (θ + 12 0^{\circ}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}]

逆变换：

𝐢_{a b c} = 𝐏^{- 1} 𝐢_{d q 0} = [\begin{matrix} \cos θ & - \sin θ & 1 \\ \cos (θ - 12 0^{\circ}) & - \sin (θ - 12 0^{\circ}) & 1 \\ \cos (θ + 12 0^{\circ}) & - \sin (θ + 12 0^{\circ}) & 1 \end{matrix}] [\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}]

派克变换也作用在定子电压与定子绕组磁链上： $𝐮_{d q 0} = 𝐏 𝐮_{a b c}$ ， $Ψ_{d q 0} = 𝐏 Ψ_{a b c}$

几何解释

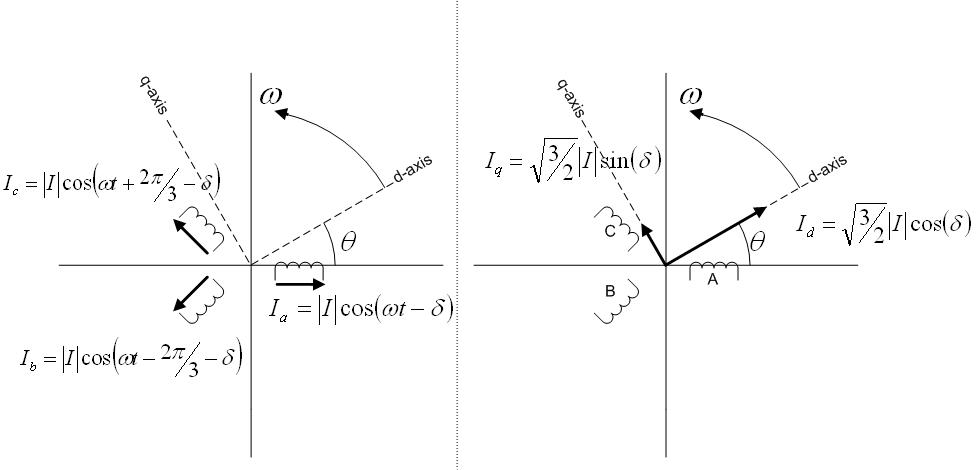上图描绘了派克变换的几何意义，定子三相电流互成120度角， $δ$ 为定子电流落后于它们对应的相电压的角度。直轴与交轴电流分别等于定子三相电流在d轴与q轴上的投影。（图中的比例系数 $\sqrt{\frac{3}{2}}$ 是由于图中所采用的是正交形式的派克变换）d-q坐标系在空间中以角速度 $ω$ 逆时针旋转，故 $θ = ω t$ 以d轴领先a相轴线的方向为正。当定子电流为三相对称的正弦交流电时， $i_{d}$ , $i_{q}$ 为直流电流， $i_{0} = 0$ 。

用派克变换化简同步发电机基本方程

变换后的磁链方程

磁链方程：

[\begin{matrix} Ψ_{a b c} \\ Ψ_{f D Q} \end{matrix}] = [\begin{matrix} 𝐋_{S S} & 𝐋_{S R} \\ 𝐋_{R S} & 𝐋_{R R} \end{matrix}] [\begin{matrix} - 𝐢_{a b c} \\ 𝐢_{f D Q} \end{matrix}]

上式中的电感系数矩阵 $𝐋_{S S}, 𝐋_{S R}, 𝐋_{R S}, 𝐋_{R R}$ 事实上都含有随时间变化的角度参数^[1]，使得方程求解困难。

现对等式两边同时左乘 $[\begin{matrix} 𝐏 \\ 𝐔 \end{matrix}]$ ，其中 $𝐔$ 为三阶单位矩阵。方程化为：

[\begin{matrix} Ψ_{d q 0} \\ Ψ_{f D Q} \end{matrix}] = [\begin{matrix} 𝐏 \\ 𝐔 \end{matrix}] [\begin{matrix} 𝐋_{S S} & 𝐋_{S R} \\ 𝐋_{R S} & 𝐋_{R R} \end{matrix}] [\begin{matrix} 𝐏^{- 1} \\ 𝐔 \end{matrix}] [\begin{matrix} - 𝐢_{a b c} \\ 𝐢_{f D Q} \end{matrix}]

[\begin{matrix} Ψ_{d q 0} \\ Ψ_{f D Q} \end{matrix}] = [\begin{matrix} {𝐏 𝐋}_{S S} 𝐏^{- 1} & {𝐏 𝐋}_{S R} \\ 𝐋_{R S} 𝐏^{- 1} & 𝐋_{R R} \end{matrix}] [\begin{matrix} - 𝐢_{d q 0} \\ 𝐢_{f D Q} \end{matrix}]

其中 ${𝐏 𝐋}_{S S} 𝐏^{- 1} = [\begin{matrix} L_{d} \\ L_{q} \\ L_{0} \end{matrix}] ≜ 𝐋_{d q 0}$ 。

① 变换后的电感系数都变为常数，可以假想dd绕组，qq绕组是固定在转子上的，相对转子静止。

② 派克变换阵对定子自感矩阵 $𝐋_{S S}$ 起到了对角化的作用，并消去了其中的角度变量。 $L_{d}, L_{q}, L_{0}$ 为其特征根。

③ 变换后定子和转子间的互感系数不对称，这是由于派克变换的矩阵不是正交矩阵。

④ $L_{d}$ 为直轴同步电感系数，其值相当于当励磁绕组开路，定子合成磁势产生单纯直轴磁场时，任意一相定子绕组的自感系数。

变换后的电压方程

电压方程：

[\begin{matrix} 𝐔_{a b c} \\ 𝐔_{f D Q} \end{matrix}] = [\begin{matrix} 𝐫_{S} \\ 𝐫_{R} \end{matrix}] [\begin{matrix} - 𝐢_{a b c} \\ 𝐢_{f D Q} \end{matrix}] + [\begin{matrix} {\dot{Ψ}}_{a b c} \\ {\dot{Ψ}}_{f D Q} \end{matrix}]

现对等式两边同时左乘 $[\begin{matrix} 𝐏 \\ 𝐔 \end{matrix}]$ ，其中 $𝐔$ 为三阶单位矩阵。方程化为：

[\begin{matrix} 𝐔_{d q 0} \\ 𝐔_{f D Q} \end{matrix}] = [\begin{matrix} 𝐫_{S} \\ 𝐫_{R} \end{matrix}] [\begin{matrix} - 𝐢_{d q 0} \\ 𝐢_{f D Q} \end{matrix}] + [\begin{matrix} {𝐏 \dot{Ψ}}_{a b c} \\ {\dot{Ψ}}_{f D Q} \end{matrix}]

由 $Ψ_{d q 0} = {𝐏 Ψ}_{a b c}$ ，

对两边求导，得 ${\dot{Ψ}}_{d q 0} = {\dot{𝐏} Ψ}_{a b c} + {𝐏 \dot{Ψ}}_{a b c}$ ，

所以 ${𝐏 \dot{Ψ}}_{a b c} = {\dot{Ψ}}_{d q 0} - {\dot{𝐏} Ψ}_{a b c} = {\dot{Ψ}}_{d q 0} - {\dot{𝐏} 𝐏}^{- 1} Ψ_{d q 0}$

其中 ${\dot{𝐏} 𝐏}^{- 1} = [\begin{matrix} ω \\ - ω \end{matrix}]$ ，令 $𝐒 = {\dot{𝐏} 𝐏}^{- 1} Ψ_{d q 0} = [\begin{matrix} ω \\ - ω \end{matrix}] [\begin{matrix} Φ_{d} \\ Φ_{q} \\ Φ_{0} \end{matrix}] = [\begin{matrix} ω Ψ_{q} \\ - ω Ψ_{d} \end{matrix}]$

于是有 $[\begin{matrix} 𝐔_{d q 0} \\ 𝐔_{f D Q} \end{matrix}] = [\begin{matrix} 𝐫_{S} \\ 𝐫_{R} \end{matrix}] [\begin{matrix} - 𝐢_{d q 0} \\ 𝐢_{f D Q} \end{matrix}] + [\begin{matrix} {\dot{Ψ}}_{d q 0} \\ {\dot{Ψ}}_{f D Q} \end{matrix}] - [\begin{matrix} 𝐒 \end{matrix}]$

上式右边第一项为绕组电阻的压降，第二项为变压器电势，第三项为发电机电势或旋转电势。

注释

↑ 定子电感矩阵 $𝐋_{S S} = [\begin{matrix} L_{a a} & M_{a b} & M_{a c} \\ M_{b a} & L_{b b} & M_{b c} \\ M_{c a} & M_{c b} & L_{c c} \end{matrix}]$ ，
其中

$L_{a a} = l_{0} + l_{2} \cos (2 θ)$

$L_{b b} = l_{0} + l_{2} \cos 2 (θ - 12 0^{\circ})$

$L_{c c} = l_{0} + l_{2} \cos 2 (θ + 12 0^{\circ})$

$M_{a b} = M_{b a} = - m_{0} - m_{2} \cos 2 (θ + 3 0^{\circ})$

$M_{b c} = M_{c b} = - m_{0} - m_{2} \cos 2 (θ - 9 0^{\circ})$

$M_{c a} = M_{a c} = - m_{0} - m_{2} \cos 2 (θ + 15 0^{\circ})$

参考书目

电机电子类科《电力系统暂态分析》，ISBN 978-7-5083-4825-4，作者：李光琦，中国电力出版社。

Template:電動機

[1] 定子电感矩阵 $𝐋_{S S} = [\begin{matrix} L_{a a} & M_{a b} & M_{a c} \\ M_{b a} & L_{b b} & M_{b c} \\ M_{c a} & M_{c b} & L_{c c} \end{matrix}]$ ，
其中

$L_{a a} = l_{0} + l_{2} \cos (2 θ)$

$L_{b b} = l_{0} + l_{2} \cos 2 (θ - 12 0^{\circ})$

$L_{c c} = l_{0} + l_{2} \cos 2 (θ + 12 0^{\circ})$

$M_{a b} = M_{b a} = - m_{0} - m_{2} \cos 2 (θ + 3 0^{\circ})$

$M_{b c} = M_{c b} = - m_{0} - m_{2} \cos 2 (θ - 9 0^{\circ})$

$M_{c a} = M_{a c} = - m_{0} - m_{2} \cos 2 (θ + 15 0^{\circ})$

[1]

派克变换

目录

定义

几何解释

用派克变换化简同步发电机基本方程

变换后的磁链方程

变换后的电压方程

注释

相關條目

参考书目

导航菜单

派克变换

定义

几何解释

用派克变换化简同步发电机基本方程

变换后的磁链方程

变换后的电压方程

注释

相關條目

参考书目

导航菜单

搜索