利萨茹曲线

示波器上的利萨茹图形

三维利萨茹图形

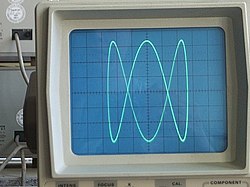
数学上，利萨茹（Template:Lang）曲线（又称利萨茹图形、李萨如图形或鲍迪奇（Template:Lang）曲线）是两个沿着互相垂直方向的正弦振动的合成的轨迹。

纳撒尼尔·鲍迪奇在1815年首先研究这一族曲线，朱尔·利萨茹在1857年作更详细研究。

数学定义

利萨茹曲线由以下参数方程定义：

$\{\begin{array}{c}x(\theta )=a\sin (\theta )\\ y(\theta )=b\sin (n\theta +\varphi )\end{array}$

其中$0\le \varphi \le \frac{\pi }{2}$，$n\ge 1$。

$n$称为曲线的参数，是两个正弦振动的频率比。若比例为有理数，则$n=\frac{q}{p}$，参数方程可以写作：

$\{\begin{array}{c}x(\theta )=a\sin (p\theta )\\ y(\theta )=b\sin (q\theta +\varphi )\\ 0\le \theta \le 2\pi \end{array}$，

其中$0\le \varphi \le \frac{\pi }{2p}$。

性质

• 若$n$为无理数，曲线在长方形$[-a,a]\times [-b,b]$中稠密。
• 若$n$为有理数，
  • 曲线是$2q$次代数曲线若$\varphi \in (0,\frac{\pi }{2p}]$对奇数$p$，或$\varphi \in [0,\frac{\pi }{2p})$对偶数$p$。
  • 曲线是$q$次代数曲线的一部份若$\varphi =0$对奇数$p$，或$\varphi =\frac{\pi }{2p}$对偶数$p$。

• 若$n$为偶数而$\varphi =\frac{\pi }{2}$，或若$n$为奇数而$\varphi =0$，则曲线是第$n$个切比雪夫多项式$T_n$的曲线的一部份。

特别情况

• 若$a=b$，$n=1$，则曲线是椭圆。
  • 若$\varphi =\frac{\pi }{2}$，则这椭圆其实是圆。
  • 若$\varphi =0$，则这椭圆其实是线段。
• 若$a=b$，$n=q=2$（所以$p=1$），则曲线是besace。
  • 若$\varphi =\frac{\pi }{2}$，则这besace是拋物线一部份。
  • 若$\varphi =0$，则这besace是一个热罗诺双纽线。

以下是利萨茹曲线的例子，其中$\varphi =0$，$a=b$, $p$是奇数，$q$是偶数，$|p-q|=1$。

• 
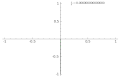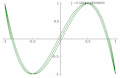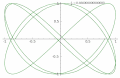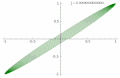
  p = 1, q = 2
• 
  p = 3, q = 2
• 
  p = 3, q = 4
• 
  p = 5, q = 4
• 
  p = 5, q = 6
• 
  p = 9, q = 8
• 

频率比1:n和n:1的情况

Δφ	1:1	1:2	1:3		2:1
0
¹/₄·π
¹/₂·π
³/₄·π
1·π
1¹/₄·π
1¹/₂·π
1³/₄·π
2·π

频率比n₁:n₂的情况

Δφ	2:3		Δφ	3:4
0			0
¹/₂·¹/₄·π			¹/₃·¹/₄·π
¹/₂·¹/₂·π			¹/₃·¹/₂·π
¹/₂·³/₄·π			¹/₃·³/₄·π
¹/₂·π			¹/₃·π
5/8·π			5/12·π
³/₄·π			¹/₂·π
7/8·π			7/12·π
1·π			²/₃·π

演示

鼠标悬浮在两个数字上时，通过滚轮可以调节数字大小。<graph mode="interactive"> {

 "width": 450,
 "height": 400,
 "signals": [
   {
     "name": "point",
     "init": 0,
     "streams": [{"type": "mousemove,touchmove","expr": "eventX()"}]
   },
   {
     "name": "r",
     "init": [1,1],
     "streams": [
       {
         "type": "@w:wheel",
         "expr": "[clamp(r[0]+(1-datum.data)*clamp(event.deltaY,-1,1),1,20),clamp(r[1]+datum.data*clamp(event.deltaY,-1,1),1,20)]"
       }
     ]
   }
 ],
 "data": [
   {
     "name": "array",
     "values": [0,1,2,3,4,5],
     "transform": [
       {"type": "cross"},
       {
         "type": "formula",
         "field": "c",
         "expr": "datum.a.data*6+datum.b.data"
       },
       {"type": "cross"},
       {
         "type": "formula",
         "field": "c",
         "expr": "datum.a.c*36+datum.b.c"
       },
       {
         "type": "formula",
         "field": "x",
         "expr": "200+cos(r[0]*datum.c*PI*2/1295)*180"
       },
       {
         "type": "formula",
         "field": "y",
         "expr": "200+sin(r[1]*datum.c*PI*2/1295+point*PI*2/400)*180"
       }
     ]
   },
   {"name": "w","values": [0,1]}
 ],
 "marks": [
   {
     "type": "line",
     "from": {"data": "array"},
     "properties": {
       "update": {
         "x": {"field": "x"},
         "y": {"field": "y"},
         "stroke": {"value": "black"},
         "strokeWidth": {"value": 2}
       }
     }
   },
   {
     "type": "rect",
     "name": "w",
     "from": {"data": "w"},
     "properties": {
       "enter": {
         "x": {"value": 400},
         "y": {"field": "data","mult": 120,"offset": 20},
         "width": {"value": 40},
         "height": {"value": 40},
         "fill": {"value": "pink"},
         "cursor": {"value": "pointer"}
       }
     }
   },
   {
     "type": "text",
     "interactive": false,
     "from": {
       "data": "w",
       "transform": [
         {
           "type": "formula",
           "field": "c",
           "expr": "r[datum.data]"
         }
       ]
     },
     "properties": {
       "update": {
         "x": {"value": 420},
         "y": {"field": "data","mult": 120,"offset": 40},
         "width": {"value": 40},
         "height": {"value": 40},
         "fill": {"value": "black"},
         "align": {"value": "center"},
         "baseline": {"value": "middle"},
         "font": {"value": "TakaoExGothic"},
         "fontSize": {"value": 20},
         "text": {"template": "Template:Datum.c"}
       }
     }
   }
 ]

} </graph>

在電子學上的應用

藉由使用利萨茹圖形可以測量出兩個信號的頻率比與相位差。

外部連結

• 利萨茹曲线的Java 3D示範 Template:Wayback