鳶形二十四面體

Template:NoteTA Template:Infobox polyhedron 在幾何學中，鳶形二十四面體（亦稱為四角化二十四面體或梯形二十四面體）是一種卡塔蘭立體，由24個鳶形組成，其對偶多面體為小斜方截半立方体。

性質

鳶形二十四面體由24個面、48條邊、26個頂點組成，其中24個面為24個全等的鳶形、48條邊中有24條等長的長邊和24條等長的短邊、26個頂點中有8個頂點是3個鳶形的公共頂點，對應的頂角是三面角；以及6個頂點是4個鳶形的公共頂點，對應的頂角是四面角；剩下的12個頂點也是4個鳶形的公共頂點，對應的頂角也是四面角，但角度與前者不同。它的對偶多面體是小斜方截半立方體。

面的組成

鳶形二十四面體由24個全等的箏-{}-形（亦稱為鳶-{}-形）所組成：

該箏形或鳶形的長短邊長比為1:(2 − Template:Sfrac) ≈ 1:Template:Val...，有3個角等角，其角度分別為(115.26°,81.58°,81.58°,81.58°)

體積與表面積

一個最短邊邊長為a的鳶形二十四面體，其表面積A、體積是V為：

$\begin{array}{cc}A& =6\sqrt{29-2\sqrt{2}}{a}^2\\ V& =\sqrt{122+71\sqrt{2}}{a}^3\end{array}$

頂點坐標

若其對偶多面體小斜方截半立方体的邊長為單位長，則對應的幾何中心位於原點的鳶形二十四面體，頂點坐標為：

$(0,0,\pm \sqrt{2})$

$(\pm \sqrt{2},0,0)$

$(0,\pm \sqrt{2},0)$

$(\pm 1,0,\pm 1)$

$(\pm 1,\pm 1,0)$

$(0,\pm 1,\pm 1)$

$(\pm \frac{4+\sqrt{2}}{7},\pm \frac{4+\sqrt{2}}{7},\pm \frac{4+\sqrt{2}}{7})$

正交投影

鳶形二十四面體有三種從頂點投影的高對稱性正交投影。後兩者的對偶圖其對稱性對應於B₂和A₂的Template:Link-en。

正交投影

投影對稱性	[2]	[4]	[6]
圖像
對偶圖像

使用

在文化中，鳶形二十四面體出現在部分藝術創作中，例如莫里茲·柯尼利斯·艾雪的藝術創作《星星》以及Template:Tsl的裝置藝術《永恆的水》。此外，亦有部份24個面的多面體骰子被設計為鳶形二十四面體的外型，其他常見的24面骰子有三角化八面體、四角化六面體、Template:Link-en、偏方二十四面體和五角二十四面體等形狀。

Template:Anchor在化學中，部分物質的結晶形狀是鳶形二十四面體。例如，在自然界中，方沸石和石榴石的晶體結構就是鳶形二十四面體，部分實驗中制備的氧化铟奈米晶體亦是這種形狀。在礦物學中，這種晶體形狀稱為偏方面體（英語：Trapezohedron），但在幾何學中偏方面體則有其他含意，表示反柱體的對偶多面體。 此外在某些情況下會結晶出較不規則的鳶形二十四面體，其在結晶學中稱為偏方二十四面體（英語：diplohedron）。

• 
  鳶形二十四面體外型的骰子。
• 
  Template:Tsl《永恆的水》
• 
  白榴石的晶體
• 
  鈣鐵榴石的晶體
• 
  方沸石的晶體
• 
  Template:Link-en的晶體

相關多面體與鑲嵌

投影到球面的鳶形二十四面體

若將鳶形二十四面體投影到球面上，如右圖所示，則其邊會與複合八面體立方體（立方體和其對偶——正八面體在空間中互相重疊組合成的結構）投影到球面上的果共用相同的稜。

鳶形二十四面體

複合八面體立方體與左圖同一個角度

鳶形二十四面體是小斜方截半立方体的對偶多面體，而小斜方截半立方体可以經由立方體或正八面體透過擴展變換來構造。其他可以由立方體或正八面體透過康威變換構造的立體及其對偶有： Template:正八面体家族

*變異的n42對稱性對偶擴展鑲嵌系列：V3.4.n.4

對稱性 Template:Link-en Template:Link-en	Template:Link-en				Template:Link-en	緊湊雙曲		仿緊雙曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
圖像 Template:Link-en	Template:AnyLink	Template:AnyLink	Template:AnyLink	V3.4.5.4	V3.4.6.4	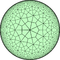Template:Link-en	V3.4.8.4	V3.4.∞.4
對偶 Template:Link-en	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	Template:Link-en	3.4.8.4	3.4.∞.4

偏方二十四面體

晶體學中的偏方二十四面體。

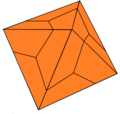
偏方二十四面體為鳶形二十四面體的一種變體，其拓樸結構與鳶形二十四面體等價。鳶形二十四面體與偏方二十四面體的拓樸結構皆與立方體每個面的正方形用兩條垂直線分成四個小正方形的結果等價。其可以投影到正八面體上並將每個三角形面分成3個鳶形。 在晶体学中，透過旋轉其三面角所形成的變體稱為dyakis dodecahedron或diploid，然而這些變體在中文文獻中皆被稱為偏方二十四面體。

Template:Link-en, Oh, 24階		Template:Link-en, Th, 12階

鳶形二十四面體圖

在圖論的數學領域中，與鳶形二十四面體相關的圖為鳶形二十四面體圖（Disdyakis Dodecahedral Graph），是鳶形二十四面體之Template:Link-en，是一個阿基米德對偶圖。

性質

Template:Anchor 鳶形二十四面體圖有48條邊和26個頂點，其中度為3的頂點有8個、度為4的頂點有18個。

其特徵多項式為：

$x^8(x^2-14){(x^2-8)}^3{(x^2-2)}^5$

參見

• 鳶形六十面體
• 四角化六面體——另外一個卡塔蘭二十四面體
• Template:Link-en

參考文獻

1. Template:The Geometrical Foundation of Natural Structure (book) (Section 3-9)
2. Template:Citation (The thirteen semiregular convex polyhedra and their duals, Page 23, Deltoidal icositetrahedron)

外部連結

• Template:Mathworld2
• Deltoidal (Trapezoidal) Icositetrahedron – Interactive Polyhedron model