Testwiki:臺灣教育專案/臺大物理系服務學習/113-1/維德曼–夫蘭茲定理

在物理學中，維德曼–夫蘭茲定理描述在金屬中電子貢獻的熱導率(κ)以及電導率(σ)間的關係，它們的比值正比於溫度(T)。

$\frac{\kappa }{\sigma }=LT$

比例係數L稱為洛倫茨係數，理論上，

$L=\frac{\kappa }{\sigma T}=\frac{{\pi }^2}{3}{\left(\frac{k_{\mathrm{B}}}{e}\right)}^2=2.44\times 10^{-8}{{\mathrm{V}}^{\mathrm{2}}\mathrm{\cdot }\mathrm{K}}^{-2},$

其中k_B 為 波茲曼常數 ， e 為 基本電荷。 此經驗定律以德國物理學家古斯塔夫·海因里希·維德曼（Gustav Heinrich Wiedemann）和魯道夫·夫蘭茲（Rudolph Franz）命名，他們於1853年由大量實驗事實發現，在相同溫度下，不同的金屬擁有大致相同的κ/σ 值。 而κ/σ 與溫度成正比則是由路德維希·洛倫茨(Ludvig Lorenz)於1872年發現。

推導

包含金屬與電池 U 的電路。 箭頭代表電場 E 以及電流密度 j 的方向。

定性上，這種關係源於金屬中熱傳導與電傳導皆涉及自由電子。

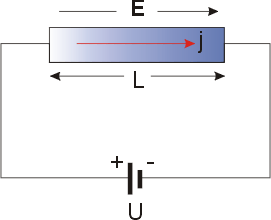
此定理的數學表達式可推導如下。金屬的電傳導是一種眾所周知的現象，源於金屬中的載子，可以按照圖中所示進行測量。 電流密度 j 被觀察到與外加電場成正比並遵守歐姆定律，即

$𝐉=\sigma 𝐄$

其中σ為特定的電導率。由於電場和電流密度都是向量，故皆以粗體表示。一般來說，電導率可以表示為二階張量(3×3 矩陣)。 這裡我們將討論限制在各向同性的電導率，故可視電導率為純量。 電阻率 是電導率的倒數。以下將會用到這兩個參數。

德魯德模型推導

保羅·德魯德(約1900年)意識到傳導率(電子、離子、熱等)的現象學描述可以寫成非常普遍的形式。儘管對傳導電子而言，該描述是不正確的，它仍可用於初步探討。

假設電子在固體中自由移動，就像理想氣體一樣。電場對電子施加的力導致電子加速：

$𝐅=-e𝐄=m\frac{d𝐯}{dt}$

$d𝐯=-\frac{e𝐄}{m}dt$

然而，這將使電子擁有恆定的加速度，並最終擁有無限的速度。因此，進一步的假設是，電子偶爾會碰到障礙物（如晶體缺陷或聲子），從而限制它們的自由移動。這決定了平均速度或漂移速度V_d。漂移速度與平均散射時間顯然相關，並有下方關係:

$\frac{d𝐯}{dt}=-\frac{e𝐄}{m}-\frac{1}{\tau }𝐯$

根據氣體動力論， $\kappa =\frac{1}{3}cn\ell ⟨v⟩$,其中$c=\frac{3}{2}{k}_{\mathrm{B}}$ 是每個電子的熱容量、 $\ell$ 是電子的平均自由徑、並且

$⟨v⟩=\sqrt{\frac{8k_{\mathrm{B}}T}{\pi m}}=\sqrt{\frac{8}{3\pi }}{v}_{\mathrm{r}\mathrm{m}\mathrm{s}}$,

是氣體中粒子的平均速率。

根據德魯德模型:

$\sigma =\frac{n{e}^2\tau }{m}=\frac{n{e}^2\ell }{m⟨v⟩}$

因此，

$\frac{\kappa }{\sigma }=\frac{cm⟨v{⟩}^2}{3e^2}=\frac{4}{\pi }\frac{k_{\mathrm{B}}^{2}T}{e^2}=0.94\times 10^{-8}{\mathrm{V}}^2{\mathrm{K}}^{-2}$,

這便是有著錯誤的比例係數 $\frac{4}{\pi }\approx 1.27$的維德曼–夫蘭茲定理。

在德魯德原先的論文中，他錯誤的使用了$⟨v^2⟩$而非$⟨v{⟩}^2$，也意外出了其他錯誤，這使他得出: $$L=3{\left(\frac{k_{\mathrm{B}}}{e}\right)}^2=2.22\times 10^{-8}{\mathrm{V}}^2{\mathrm{K}}^{-2}$$ 這與實驗值非常接近。事實上，這是由三個錯誤所造成的: 誤用了一個為2的因子、每個電子的比熱事實上比$\frac{3}{2}{k}_{\mathrm{B}}$小了約100倍、以及電子的方均根速率事實上約是100倍大。

自由電子模型

考慮量子效應後，如自由電子模型一樣，電子的熱容量、平均自由徑和平均速度都需被修改，比例常數也會被修正為$\frac{{\pi }^2}{3}\approx 3.29$，這與實驗值一致。

溫度依賴性

值 L₀ = Template:Val是由於熱和電荷在極低溫下 ($T\to 0$ K)皆是由相同的準粒子(電子及電洞)傳輸。在有限的溫度下，比值$L=\kappa /(\sigma T)$ 會與理論值 L₀有偏差，這是由兩種機制造成的:(1)有其他的熱載子，如聲子或磁振子 (2)非彈性散射。在溫度接近 0 K 時，非彈性散射的效應將變弱，並促成較大的q散射值(如圖中的a軌跡)。每當電子傳輸時，熱激發也會被一起傳輸，這使洛倫茨係數L = L₀。注意到在完美的金屬中，非彈性散射在極限$T\to 0$ K 時將不存在，且有$\kappa \to 0;L\to 0$。在有限的溫度下，較小的q散射值是可能的(如圖中的b軌跡)，並且電子可以在熱激發不被傳輸下被傳輸，因此有L(T) < L₀。在更高的溫度下，聲子對於系統熱傳導的貢獻變得重要，這可導致L(T) > L₀。在溫度高於德拜溫度時，聲子對熱傳輸的貢獻恆定，並且比值 L(T) 再度恆定。

對維德曼–夫蘭茲定理重要的各種散射過程。

理論的局限性

實驗表明，雖然L的值大致恆定，但對於各材料來說並不完全相同。基泰爾 在書中給出了一些L的值，範圍從0 °C 時銅的L =2.23×10⁻⁸V²K⁻² 到100 °C時鎢的 L =3.2×10⁻⁸V²K⁻²。Rosenberg 指出，維德曼–夫蘭茲定理通常適用於高溫和低溫（即幾克耳文），但在中間溫度下可能不成立。

在許多高純度金屬中，電導率和熱導率都會隨著溫度降低而上升。然而，在某些材料（例如銀或鋁）中， L的值也可能隨著溫度的升高而降低。在純度最高的銀樣品中，在極低的溫度下，L值可下降10倍之多。

在簡併半導體中，洛倫茨係數L高度依賴於某些系統參數: 維數、原子間相互作用強度和費米能階。已知至少在下列情況下該定理無效或洛倫茨係數的值會降低：操縱電子的態密度、改變超晶格和具有關聯載子(correlated carriers)的材料中的摻雜密度和沉積層厚度。在熱電材料中，也存在著由於邊界條件而進行的校正，特別是斷路與通路。

違反定理的現象

2011年，N. Wakeham等人發現準一維鋰鉬紫青銅Li_0.9Mo₆O₁₇的金屬相的霍爾熱導率與霍爾電導率比值隨溫度的降低而發生變化，其值比遵循維德曼–夫蘭茲定理的傳統金屬高出 5 個數量級。 這是由自旋–電子分離引起的，並且其中的電子行為類似拉廷格液體。

2016年，柏克萊大學的S. Lee等人領導的一項研究中也發現，在VO₂奈米樑的絕緣-金屬相轉變附近，出現嚴重違反維德曼–夫蘭茲定理的現象。在金屬相中，電子對熱導率的貢獻比維德曼-弗朗茲定律預期的要小得多。結果可以用強關聯系統中電荷和熱的獨立傳播來解釋。

分子系統

2020年，Galen Craven和Abraham Nitzan推導出分子系統的維德曼–夫蘭茲定理，其中的電子傳導不同於金屬，是由分子位點間的電子轉移主導。 分子系統的維德曼–夫蘭茲定理為

$\frac{\kappa }{\sigma }=L_{\text{M}}\frac{\lambda }{k_{\mathrm{B}}}$

其中

$L_{\text{M}}=\frac{1}{2}{\left(\frac{k_{\mathrm{B}}}{e}\right)}^2$

是分子的洛倫茨係數 ， $\lambda$ 則是電子轉移的重組能。

參見

• 德魯德模型