餘弦定理

一個三角形

Template:三角学 餘弦定理是三角形中三邊長度與一個角的余弦值（$\cos$）的數學式，余弦定理指的是：

$c^2=a^2+b^2-2ab\cos \gamma$

同樣，也可以將其改為：

$b^2=c^2+a^2-2ca\cos \beta$

$a^2=b^2+c^2-2bc\cos \alpha$

其中$c$是$\gamma$角的對邊，而$a$和$b$是$\gamma$角的鄰邊。

勾股定理則是余弦定理的特殊情況，當$\gamma$為$90^{\circ }$時，$\cos \gamma =0$，等式可被簡化為

$c^2=a^2+b^2$

當知道三角形的兩邊和一角時，余弦定理可被用來計算第三邊的長，或是當知道三邊的長度時，可用來求出任何一個角。

歷史

一個鈍三角形和它的高。

余弦定理的歷史可追溯至公元三世紀前歐幾里得的幾何原本，在書中將三角形分為鈍角和銳角來解釋，這同時對應現代數學中余弦值的正負。根據幾何原本第二卷的命題12和13，並參考右圖，以現代的數學式表示即為：

$\stackrel{2}{\stackrel{‾}{AB}}=\stackrel{2}{\stackrel{‾}{CA}}+\stackrel{2}{\stackrel{‾}{CB}}+2(\overline{CA})(\overline{CH})$

其中$\overline{CH}=\overline{BC}\cos (\pi -\gamma )=-\overline{BC}\cos \gamma$，將其帶入上式得到：

$\stackrel{2}{\stackrel{‾}{AB}}=\stackrel{2}{\stackrel{‾}{CA}}+\stackrel{2}{\stackrel{‾}{CB}}-2(\overline{CA})(\overline{BC})\cos \gamma$

證明

三角函數

具有垂直線的銳角三角形

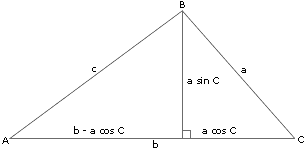
見右圖，在$c$上做高可以得到（投影定理）：

$c=a\cos \beta +b\cos \alpha$

將等式同乘以c得到：

$c^2=ac\cos \beta +bc\cos \alpha$

運用同樣的方式可以得到：

$a^2=ac\cos \beta +ab\cos \gamma$

$b^2=bc\cos \alpha +ab\cos \gamma$

將$c^2$的右式取代：

$c^2=ac\cos \beta +bc\cos \alpha =(a^2-ab\cos \gamma )+(b^2-ab\cos \gamma )=a^2+b^2-2ab\cos \gamma$

勾股定理

勾股定理之一

設$\mathrm{△}ABC$中，$\overline{AB}=c$，$\overline{BC}=a$，$\overline{AC}=b$。過$B$點作$AC$的垂線，垂足為$D$，如果$D$在$AC$內部，則$BD$的長度為$a\sin C$，$DC$的長度為$a\cos C$，$AD$的長度為$b-a\cos C$。根據勾股定理：

$c^2=(a\sin C{)}^2+(b-a\cos C{)}^2$

$c^2=a^2{\sin }^{2}C+b^2-2ab\cos C+a^2{\cos }^{2}C$

$c^2=a^2({\sin }^{2}C+{\cos }^{2}C)+b^2-2ab\cos C$

$c^2=a^2+b^2-2ab\cos C$

如果$D$在$AC$的延長線上，證明是類似的。同理可以得到其他的等式。

勾股定理之二

證明所用的三角形

設$\mathrm{△}ABC$中，$\overline{AB}=c$，$\overline{BC}=a$，$\overline{AC}=b$。過$B$點作$\overline{AC}$的垂線，垂足為$D$，設$\overline{AD}=x$，則$\overline{CD}=b-x$，根據勾股定理：

$c^2-x^2=\stackrel{2}{\stackrel{‾}{BD}}=a^2-(b-x{)}^2$

$c^2-x^2=a^2-b^2-x^2+2bx$

$c^2=a^2-b^2+2bx$

$x=\frac{b^2+c^2-a^2}{2b}$

$\cos A=\frac{x}{c}=\frac{b^2+c^2-a^2}{2bc}$

如果$D$在$\overline{AC}$的延長線上，證明是類似的。同理可以得到其他的等式。

應用

餘弦定理是解三角形中的一個重要定理。

求邊

餘弦定理可以簡單地變形成：

$a=\sqrt{b^2+c^2-2bc\cos A}$

$b=\sqrt{c^2+a^2-2ac\cos B}$

$c=\sqrt{a^2+b^2-2ab\cos C}$

因此，如果知道了三角形的兩邊及其夾角，可由餘弦定理得出已知角的對邊。

求角

余弦定理可以简单地变形成：

$\cos A=\frac{b^2+c^2-a^2}{2bc}$

$\cos B=\frac{c^2+a^2-b^2}{2ca}$

$\cos C=\frac{a^2+b^2-c^2}{2ab}$

因為餘弦函數在$(\mathrm{0},\pi )$上的單調性，可以得到：

$\mathrm{\angle }A=\arccos \frac{b^2+c^2-a^2}{2bc}$

$\mathrm{\angle }B=\arccos \frac{c^2+a^2-b^2}{2ca}$

$\mathrm{\angle }C=\arccos \frac{a^2+b^2-c^2}{2ab}$

因此，如果已知三角形的三邊，可以由餘弦定理得到三角形的三個內角。

參見

• 三角形
• 勾股定理
• 正弦定理
• 正切定理
• 角平分線長公式
• 中線長公式