螺旋函数

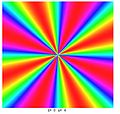
swirl function Maple plot

螺旋函数(Swirl function)是一个以三角函数定义的特殊函数：

$S(k,n,r,\theta )=sin(k*cos(r)-n*\theta )$

其中k,n均为整数。k与螺旋叶的长度与形状有关，n为螺旋的叶片数。

对称性

镜像对称

• $S(k,n,r,\theta )$与$S(k,-n,r,\theta )$ 互为镜像对称.
• $f(-k,n,r,\theta )=-f(k,n,r,-\theta )$
• $f(-k,n,r,\theta )=-f(k,-n,r,\theta )$
• $f(-k,-n,r,\theta )=-f(k,n,r,\theta )$
• $f(-k,n,r,-\theta )=-f(k,n,r,\theta )$
• $f(-k,n,r,\theta )=-f(k,n,-r,-\theta )$

• $f(-k,n,-r,-\theta )=-f(k,n,r,\theta )$

• $f(-k,-n,-r,\theta )=-f(k,n,r,\theta )$

• $f(-k,n,-r,-\theta )=-f(k,n,r,\theta )$

全对称

• $f(k,-n,r,\theta )=f(k,n,r,-\theta )$
• $f(k,-n,r,-\theta )=f(k,n,r,\theta )$

• $f(k,n,-r,\theta )=f(k,n,r,\theta )$

• $f(k,n,-r,\theta )=f(k,n,r,\theta )$

• $f(k,n,-r,\theta )=f(k,-n,r,-\theta )$

• $f(k,-n,-r,-\theta )=f(k,n,r,\theta )$
• $f(k,n,-r,\theta )-f(k,n,r,\theta )$

旋转对称

$S(k,n,r,\theta +\frac{2\pi }{n})=S(k,n,r,\theta )$

级数展开

$S(k,n,r,\theta )\approx sin(k-n*\theta )-(1/2)*cos(k-n*\theta )*k*r^2+(-(1/8)*sin(k-n*\theta )*k^2+(1/24)*cos(k-n*\theta )*k)*r^4+((1/48)*sin(k-n*\theta )*k^2+cos(k-n*\theta )*(-(1/720)*k+(1/48)*k^3))*r^6+O(r^8)$

$S(k,n,r,\theta )\approx sin(k*cos(r))-cos(k*cos(r))*n*\theta -(1/2)*sin(k*cos(r))*n^2*{\theta }^2+(1/6)*cos(k*cos(r))*n^3*{\theta }^3+(1/24)*sin(k*cos(r))*n^4*{\theta }^4-(1/120)*cos(k*cos(r))*n^5*{\theta }^5-(1/720)*sin(k*cos(r))*n^6*{\theta }^6+(1/5040)*cos(k*cos(r))*n^7*{\theta }^7+(1/40320)*sin(k*cos(r))*n^8*{\theta }^8+O({\theta }^9)$

与其他特殊函数关系

• $S(k,n,r,\theta )=\frac{(nx\arccos \left(x\right)+1/2\pi )\mathrm{K}\mathrm{u}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{M}(1,2,i(2nx\arccos \left(x\right)+\pi ))}{{\mathrm{e}}^{1/2i(2nx\arccos \left(x\right)+\pi )}}$

• $S(k,n,r,\theta )=\frac{-i(2nx\arccos \left(x\right)+\pi )\mathrm{W}\mathrm{h}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{M}(0,1/2,i(2nx\arccos \left(x\right)+\pi ))}{4nx\arccos \left(x\right)+2\pi }$

• $S(k,n,r,\theta )=\frac{-1/2i(-1+{\mathrm{e}}^{i(2nx\arccos \left(x\right)+\pi )})}{{\mathrm{e}}^{1/2i(2nx\arccos \left(x\right)+\pi )}}$

• $S(k,n,r,\theta )=-n{x}^2𝐻𝑒𝑢𝑛𝐵(2,0,0,0,\sqrt{2}\sqrt{1/2i(2nx(1/2\pi -x𝐻𝑒𝑢𝑛𝐶(0,1/2,0,0,1/4,\frac{x^2}{x^2-1})\frac{1}{\sqrt{1-x^2}})+\pi )})𝐻𝑒𝑢𝑛𝐶(0,1/2,0,0,1/4,\frac{x^2}{x^2-1})\frac{1}{\sqrt{1-x^2}}{\left({\mathrm{e}}^{-1/2i(-nx\pi \sqrt{1-x^2}+2n{x}^2𝐻𝑒𝑢𝑛𝐶(0,1/2,0,0,1/4,\frac{x^2}{x^2-1})-\pi \sqrt{1-x^2})\frac{1}{\sqrt{1-x^2}}}\right)}^{-1}+1/2\pi (nx+1)𝐻𝑒𝑢𝑛𝐵(2,0,0,0,\sqrt{2}\sqrt{1/2i(2nx(1/2\pi -x𝐻𝑒𝑢𝑛𝐶(0,1/2,0,0,1/4,\frac{x^2}{x^2-1})\frac{1}{\sqrt{1-x^2}})+\pi )}){\left({\mathrm{e}}^{-1/2i(-nx\pi \sqrt{1-x^2}+2n{x}^2𝐻𝑒𝑢𝑛𝐶(0,1/2,0,0,1/4,\frac{x^2}{x^2-1})-\pi \sqrt{1-x^2})\frac{1}{\sqrt{1-x^2}}}\right)}^{-1}$

图例

螺旋叶数与镜像对称

• 
  7,-2
• 
  7,2
• 
  7,-4
• 
  7,4
• 
  7,-6
• 
  7,6
• 
  7,-8
• 
  7,8
• 
  7,-10
• 
  7,10
• 
  7,-12
• 
  7,12

螺旋叶形

• 
  0,4
• 
  1,4
• 
  2,4
• 
  7,4
• 
  -5,4
• 
  -9,4
• 
  30,4