样条插值

在数值分析这个数学分支中，样条插值是使用一种名為样条的特殊分段多项式进行插值的形式。由于样条插值可以使用低阶多项式样条实现较小的插值误差，这样就避免了使用高阶多项式所出现的龙格现象，所以样条插值得到了流行。

样条插值

使用多项式插值，对给定数据集进行插值的n阶多项式就被给定数据点所唯一地定义出来。但是，对同样的数据进行插值的n阶样条并不是唯一的，为了构建一个唯一的样条插值式它还必须满足另外n-1个自由度。

线性样条插值

线性样条插值是最简单的样条插值。数据点使用直线进行连接，结果样条是一个多边形。

从代数的角度来看，每个S_i 都是一个如下

$S_i(x)=y_i+\frac{y_{i+1}-y_i}{x_{i+1}-x_i}(x-x_i)$

的线性函数。 样条在每个数据点都必须连续，即

$S_i(x_{i+1})=S_{i+1}(x_{i+1})\text{ , }i=1,\dots n-1$

我们很容易得到

$S_{i-1}(x_i)=y_{i-1}+\frac{y_i-y_{i-1}}{x_i-x_{i-1}}(x-x_{i-1})=y_i$

$S_i(x_i)=y_i+\frac{y_{i+1}-y_i}{x_{i+1}-x_i}(x-x_i)=y_i$

所以以上论述成立。

二次样条插值

二次样条插值可以构建为

$S_i(x)=y_i+z_i(x-x_i)+\frac{z_{i+1}-z_i}{2(x_{i+1}-x_i)}(x-x_i{)}^2$

通过选择$z_0$，然后用递推关系就可以得到系数：

$z_{i+1}=-z_i+2\frac{y_{i+1}-y_i}{x_{i+1}-x_i}$

三次样条插值

对于$n+1$给定点的数据集$\{x_i\}$，我们可以用$n$段三次多项式在数据点之间构建一个三次样条。如果

$S(x)=\{\begin{array}{c}{S}_0(x),x\in [x_0,x_1]\\ S_1(x),x\in [x_1,x_2]\\ \cdots \\ S_{n-1}(x),x\in [x_{n-1},x_n]\end{array}$

表示对函数$f$进行插值的样条函数，那么需要：

• 插值特性，$S(x_i)=f(x_i)$
• 样条相互连接，$S_{i-1}(x_i)=S_i(x_i),i=1,\dots ,n-1$
• 两次连续可导，$S{\text{'}}_{i-1}(x_i)=S{\text{'}}_i(x_i)$ 以及 $S^{\prime }{\text{'}}_{i-1}(x_i)=S^{\prime }{\text{'}}_i(x_i),i=1,\dots ,n-1$.

由于每个三次多项式需要四个条件才能确定曲线形状，所以对于组成$S$的$n$个三次多项式来说，这就意味着需要$4n$个条件才能确定这些多项式。但是，插值特性只给出了$n+1$个条件，内部数据点给出$n+1-2=n-1$个条件，总计是$4n-2$个条件。我们还需要另外两个条件，根据不同的因素我们可以使用不同的条件。

其中一项选择条件可以得到给定$u$与$v$的钳位三次样条，

$S^{\prime }(x_0)=u$

$S^{\prime }(x_k)=v$

另外，我们可以设

$S^{″}(x_0)=S^{″}(x_n)=0$.

这样就得到自然三次样条。自然三次样条几乎等同于样条设备生成的曲线。

在这些所有的二次连续可导函数中，钳位与自然三次样条可以得到相对于待插值函数f的最小震荡。

如果选择另外一些条件，

$S(x_0)=S(x_n)$

$S^{\prime }(x_0)=S^{\prime }(x_n)$

$S^{″}(x_0)=S^{″}(x_n)$

可以得到周期性的三次样条。

如果选择，

$S(x_0)=S(x_n)$

$S^{\prime }(x_0)=S^{\prime }(x_n)$

$S^{″}(x_0)=f^{\prime }(x_0),S^{″}(x_n)=f^{\prime }(x_n)$

可以得到complete三次样条。

三次样条的最小性

三次样条有另外一个非常重要的解释，实际上它是在索伯列夫空间$H^2([a;b])$最小化泛函

$J(f)=\underset{a}{\overset{b}{\int }}|f^{″}(x){|}^{2}dx$

的函数。

泛函$J$包含对于函数$f(x)$全部曲率$\left|\frac{f^{″}(x)}{(1+f^{\prime }(x{)}^2{)}^{\frac{3}{2}}}\right|$的近似，样条是$f(x)$最小曲率的近似。

由于弹性条的总体能量与曲率成比例，所以样条是受到$n$个点约束的弹性条的最小能量形状。样条也是基于弹性条设计的工具。

使用自然三次样条的插值

它可以定义为

$S_i(x)=\frac{z_{i+1}(x-x_i{)}^3+z_i(x_{i+1}-x{)}^3}{6h_i}+(\frac{y_{i+1}}{h_i}-\frac{h_i}{6}{z}_{i+1})(x-x_i)+(\frac{y_i}{h_i}-\frac{h_i}{6}{z}_i)(x_{i+1}-x)$

以及

$h_i=x_{i+1}-x_i$.

通过解下面的方程可以得到它的系数。

$\{\begin{array}{c}{z}_0=0\\ h_{i-1}{z}_{i-1}+2(h_{i-1}+h_i)z_i+h_i{z}_{i+1}=6(\frac{y_{i+1}-y_i}{h_i}-\frac{y_i-y_{i-1}}{h_{i-1}})\\ z_n=0\end{array}$

示例

线性样条插值

假设要为带有节点

$(x_0,f(x_0))=(x_0,y_0)=(-1,e^{-1})$

$(x_1,f(x_1))=(x_1,y_1)=(-\frac{1}{2},e^{-\frac{1}{4}})$

$(x_2,f(x_2))=(x_2,y_2)=(0,1)$

$(x_3,f(x_3))=(x_3,y_3)=(\frac{1}{2},e^{-\frac{1}{4}})$

$(x_4,f(x_4))=(x_4,y_4)=(1,e^{-1})$

的函数

$f(x)=e^{-x^2}$

找一个线性样条。直接代入样条公式，我们得到如下样条：

$S(x)=\{\begin{array}{cc}{e}^{-1}+2(e^{-\frac{1}{4}}-e^{-1})(x+1)& x\in [-1,-\frac{1}{2}]\\ e^{-\frac{1}{4}}+2(1-e^{-\frac{1}{4}})(x+\frac{1}{2})& x\in [-\frac{1}{2},0]\\ 1+2(e^{-\frac{1}{4}}-1)x& x\in [0,\frac{1}{2}]\\ e^{-\frac{1}{4}}+2(e^{-1}-e^{-\frac{1}{4}})(x-\frac{1}{2})& x\in [\frac{1}{2},1]\end{array}$

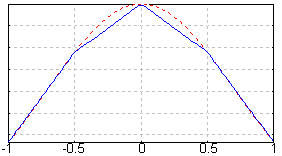
样条函数（蓝线）以及所近似的函数（红点）如下图所示：

二次样条插值

下图是一个k=4的样条函数（蓝线）与所近似的函数（红线）的例子：

参见

• 三次埃尔米特样条
• NURBS