星形多邊形

在幾何學中，星形多邊形是一種外觀有數個向外凸起的非凸多邊形。目前幾何學上尚未有一個廣泛被接受的星形多邊形定義，目前較常見的定義為存在頂點不和相鄰頂點連接的多邊形，或者從一般多邊形透過截角或延長邊並使其相交所形成的形狀。目前有被從多個角度進行研究的星形多邊形只有星形正多邊形。數學家Template:Link-en指出了兩種由克卜勒提出的定義：一種是具有自相交稜的星形正多邊形，且自相交的稜不產生新的頂點，另一種是等邊的簡單凹多邊形。

命名

星形多邊形一般有許多向外突出的角，一般依照其向外突出之角的數量命名，如五角星，部分文獻將之稱為一個芒，整體形狀以芒數命名，如五芒星與六芒星。

簡單等邊星形多邊形

若一星形多邊形是一個簡單多邊形或邊不相交的多邊形，則該星形多邊形不可能為星形正多邊形，因為若將星形正多邊形的相交邊移除，則其不再正多邊形，但可以形成等邊多邊形。這類等邊多邊形通常由2個落在半徑不同的圓上之頂點交錯連接構成。數學家Template:Link-en在其著作《Tilings and Patterns》中將這類多邊形以符號$|x|$表示由星形多邊形$\{x\}$移除相交線段後構成的星形多邊形，例如星形多邊形$\{\frac{n}{d}\}$移除位於內部的線段後的結果計為$|\frac{n}{d}|$或$\{n\alpha \}$表達一個內角$\alpha <180(1-\frac{2}{n})$度的n角星。

簡單等邊星形多邊形

|n/d| {nα}	{330°}	{630°}	|5/2| {536°}	{445°}	|8/3| {845°}	|6/2| {660°}	{572°}
α	30°		36°	45°		60°	72°
β	150°	90°	72°	135°	90°	120°	144°
等邊星形多邊形
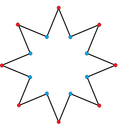
對應的星形正多邊形	{12/5}		{5/2}	{8/3}		2{3} Template:Link-en	{10/3}

星形正多邊形

{5/2}

{7/2}

{7/3}...

星形正多邊形包括五角星和八角星等等，n角星的施萊夫利符號為{n/m}，其中m是小於n/2且和n互質的正整數。托馬斯·布拉德華是最早系統性地對星形正多邊形的研究的學者，後來约翰内斯·开普勒也做了類似的研究。

參見

• 星形多面體