时钟问题

2:20时指针之间的角度关系

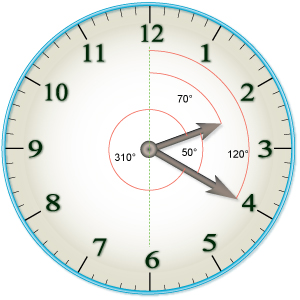
时钟问题（又称钟表问题）是一类与时钟有关的数学问题。这类题常见于中国大陆小学奥林匹克数学，以及中国国家公务员考试中。

概述

求解这类型题的关键在于找到时间与角之间的关系。解题中角一般用角度制表示，时间使用十二小时制。求解技巧有列方程、使用追及问题模型等。

公式

时针在12小时内转过1周（360°），故时针1小时转30°，1分钟转0.5°。分针1小时转360°，故1分钟转6°。由此可以推出以下公式：

当时间为H时M分时，时针与12点钟方向夹角的角度数（${\theta }_{\text{hr}}$）为：

${\theta }_{\text{hr}}=\frac{1}{2}(60H+M)$

分针与12点钟方向夹角的角度数（${\theta }_{\text{min.}}$）为：

${\theta }_{\text{min.}}=6M$

时针与分针之间的夹角为：

$\begin{array}{cc}\mathrm{\Delta }\theta & =|{\theta }_{\text{hr}}-{\theta }_{\text{min.}}|\\ & =|\frac{1}{2}(60H+M)-6M|\\ & =|\frac{1}{2}(60H-11M)|\end{array}$

例题

2:00到3:00之间，哪一时刻时针与分针重合？

解：当且仅当${\theta }_{\text{hr}}={\theta }_{\text{min.}}$时，时针与分针重合。依公式有，

$\begin{array}{cc}\frac{1}{2}(60H+M)& =6M\\ 11M& =60H\\ M& =\frac{60}{11}H\end{array}$

代入$H=2$，得$M=10\frac{10}{11}$。即2时$10\frac{10}{11}$分，时针与分针重合。

参见

• 时钟