扭稜四角反角柱

Template:NoteTA Template:Infobox polyhedron 扭稜四角反角柱（英文：Snub square antiprism）是詹森多面體的其中一個，其所引為J₈₅^[1]。它無法由柏拉圖立體（正多面體）和阿基米得立體（半正多面體）經過切割、增補而得來。扭稜四角反角柱是詹森多面體中的基本立體之一。詹森多面體是凸多面體，面皆由正多邊形組成但不屬於均勻多面體，共有92種。這些立體最早在1966年由Template:Tsl（Norman Johnson）命名並給予描述^[2]。

性質

扭稜四角反角柱共由26個面、40條邊和16頂點所組成^[3]^[4]^[5]。在其26個面中，有24個三角形和2個正方形^[3]。在其16個頂點中，有8個頂點是5個三角形的公共頂點^[5]，在頂點圖中可以用[3⁵]來表示^[6]、另外8個頂點是4個三角形和1個正方形的公共頂點^[5]，在頂點圖中可以用[3⁴,4]來表示^[6]。

構造

形如其名地，扭稜四角反角柱可以透過將四角反角柱套用扭稜變換來構造。在施萊夫利符號中可以表示為ssTemplate:Mset，其中sTemplate:Mset是四角反角柱^[7]，其中的扭稜是考克斯特扭稜；而在康威扭稜中，扭稜四角反角柱可以透過將四角錐套用康威扭稜來構造，在康威多面體表示法中可以表示為sY4^[8]。

體積與表面積

若一個扭稜四角反角柱邊長為 $a$ ，則其表面積 $A$ 為：^[9]

A = (2 + 6 \sqrt{3}) a^{2} \approx 12.39230 a^{2},

^[10]

而其體積 $V$ 為：

V = ξ a^{3},

其中 $ξ \approx 3.60122$ 是下列多項式的最大實根：

531441 x^{12} - 85726026 x^{8} - 48347280 x^{6} + 11588832 x^{4} + 4759488 x^{2} - 892448 .

^[11]

頂點座標

令 $k$ 為下列三次式的正實根，約為 $k \approx 0.82354$ ：

9 x^{3} + 3 \sqrt{3} (5 - \sqrt{2}) x^{2} - 3 (5 - 2 \sqrt{2}) x - 17 \sqrt{3} + 7 \sqrt{6} .

和h約為 $h \approx 1.35374$ ：

h = \frac{\sqrt{2} + 8 + 2 \sqrt{3} k - 3 (2 + \sqrt{2}) k^{2}}{4 \sqrt{3 - 3 k^{2}}} .

則邊長為2的扭稜四角反角柱的頂點座標由下列頂點的軌道的並集在繞z軸旋轉90°和繞垂直於z軸並與x軸夾角22.5°的直線旋轉180°所產生的空間對稱群之群作用下給出：^[12]

(1, 1, h), (1 + \sqrt{3} k, 0, h - \sqrt{3 - 3 k^{2}})

扭稜反角柱

類似的造方式之多面體還有扭稜三角反角柱（施萊夫利符號：ssTemplate:Mset）為經過扭稜變換的三角反角柱（可以視為一個對稱性較低的正八面體），其結果為偽二十面體（可以視為一個對稱性較低的正二十面體）。另一個為扭稜五角反角柱（施萊夫利符號：ssTemplate:Mset）甚至是更高邊數的扭稜反角柱，但其結果不會是由正三角形構成的凸多面體。邊數更少的扭稜二角反角柱（施萊夫利符號：ssTemplate:Mset）對應另一個詹森多面體——扭稜鍥形體，但必須在二角反角柱中保留兩個退化的對角面（以紅色繪製）。這些都可以視為一系列扭稜反角柱無窮序列的一項。^[7]

扭稜反角柱
對稱性	D_2d, [2⁺,4], (2*2)	D_3d, [2⁺,6], (2*3)	D_4d, [2⁺,8], (2*4)	D_5d, [2⁺,10], (2*5)
反角柱	s{2,4} A2 Template:CDD （頂點：4、邊：8、面：6）	s{2,6} A3 Template:Wayback Template:CDD （頂點：6、邊：12、面：8）	s{2,8} A4 Template:Wayback Template:CDD （頂點：8、邊：16、面：10）	s{2,10} A5 Template:Wayback Template:CDD （頂點：10、邊：20、面：12）
截角反角柱	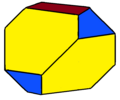ts{2,4} tA2 （頂點：16、邊：24、面：10）	ts{2,6} tA3 Template:Wayback （頂點：24、邊：36、面：14）	Template:Link-en tA4 Template:Wayback （頂點：32、邊：48、面：18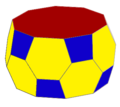）	ts{2,10} tA5 Template:Wayback （頂點：40、邊：60、面：22）
對稱性	D₂, [2,2]⁺, (222)	D₃, [3,2]⁺, (322)	D₄, [4,2]⁺, (422)	D₅, [5,2]⁺, (522)
扭稜反角柱	J84	二十面體	J85	凹
		sY3 Template:Wayback = HtA3	sY4 Template:Wayback = HtA4	sY5 Template:Wayback = HtA5
	ss{2,4} （頂點：8、邊：20、面：14）	ss{2,6} （頂點：12、邊：30、面：20）	ss{2,8} （頂點：16、邊：40、面：26）	ss{2,10} （頂點：20、邊：50、面：32）