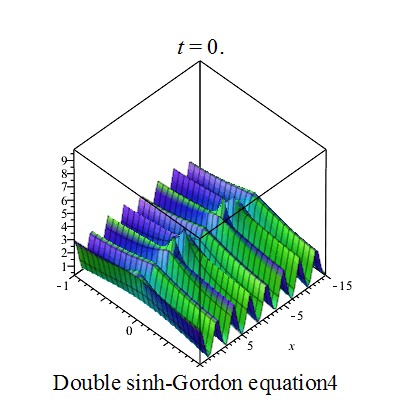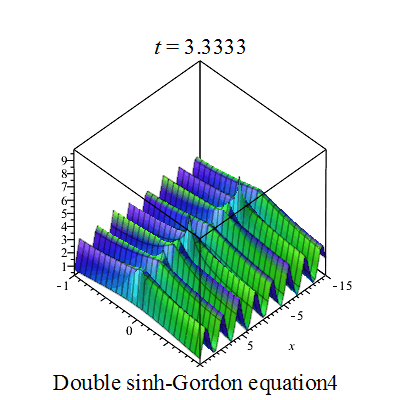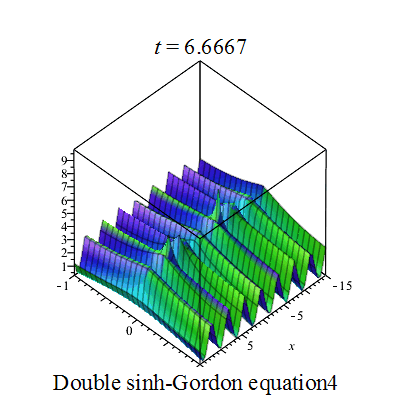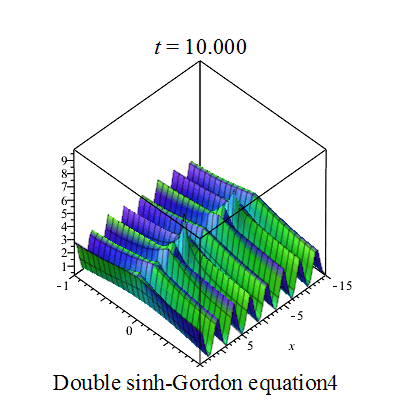
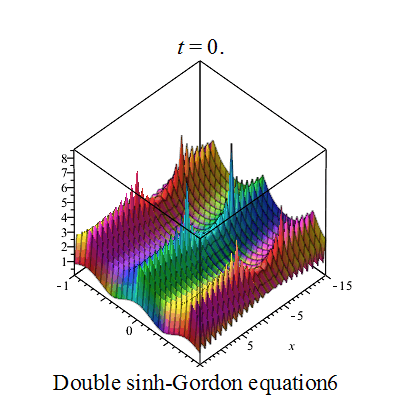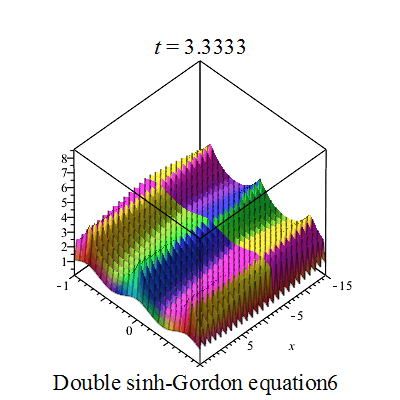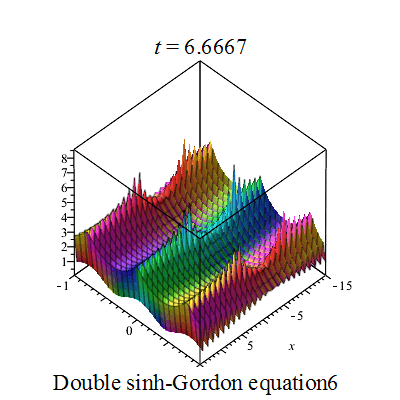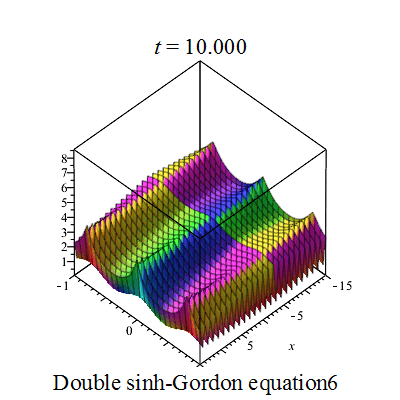
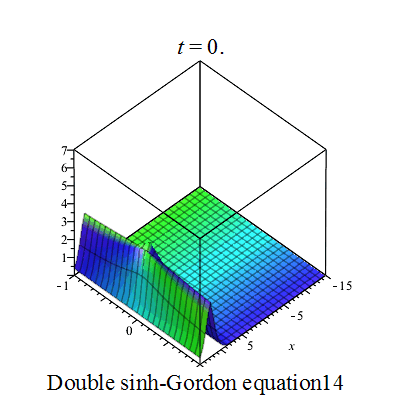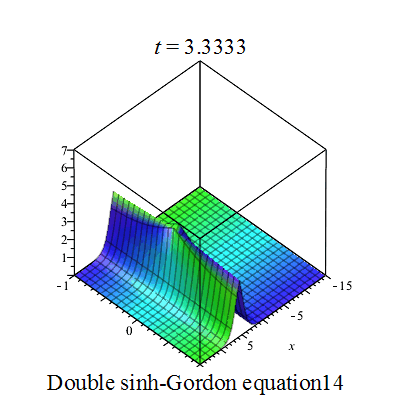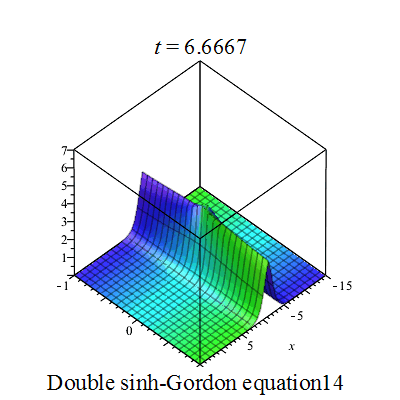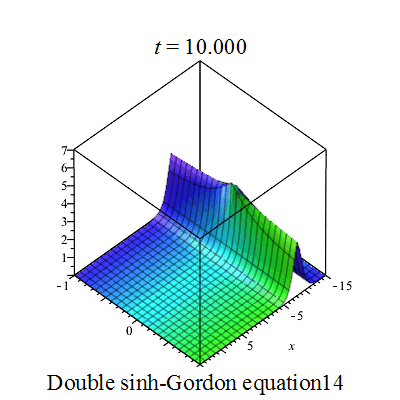
双重sinh-Gordon方程(Double sinh-Gordon equation)是一个非线性偏微分方程。[1][2][3][4][5].
行波解
其中
特解
行波图
参考文献
- ↑ Andrei D. Polyanin, Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS SECOND EDITION CRC Press, A Chapman & Hall Book ISBN 9781420087239
- ↑ Zeitschrift Für Naturforschung: A journal of physical sciences 2004 p933-937
- ↑ A. M. WAZWAZ Exact solutions to the double sinh-gordon equation by the tanh method and a variable separated ODE method,Computers & Mathematics with Applications,Volume 50, Issues 10–12, November–December 2005, Pages 1685–1696
- ↑ Issues in Logic, Operations, and Computational Mathematics and Geometry 2013 p484
- ↑ Mathematical Reviews - Page 3708 2007