二複合二十面體

完全扭稜八面體, β{3,4}

在幾何學中，二複合二十面體是指由2個正二十面體複合而成的複合多面體。這種立體具備八面體群對稱性。

作為完全扭稜立體

二複合二十面體可以視作一種完全扭稜（holosnub）的立體，就類似正四面體可以扭稜成結構等價於正二十面體的扭稜四面體一般。作為一個完全扭稜立體的二複合二十面體在施萊夫利符號中可以用β{3,4}表示，在考克斯特符號中可以用Template:CDD表示。其中，符號β表示完全扭稜。

對稱性

二複合二十面體由2個正二十面體組成，每個正二十面體由20個三角形組成。這40個三角形在對稱群的群作用下分解為兩條軌道：其中16個三角形兩兩共面落在八面體平面中，而其他24個三角形各自位於獨立的平面中。其他具備二十面體對稱性之立體的二複合體也具有類似特性。

相關多面體

二複合二十面體除了八面群對稱性的複合結構外，還有另外兩種複合結構。

• 
  二複合二十面體均勻複合體
• 
  沿著面幾何中心到對應面幾何中心的軸轉的二複合體
• 
  沿著頂點到點的軸轉的二複合體

二複合十二面體

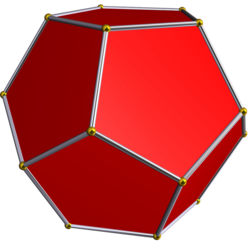
Template:Infobox polyhedron 二複合二十面體是二複合十二面體的對偶多面體。二複合十二面體顧名思義即2個正十二面體的複合體。其可以透過將正十二面體沿著內接立方體的4重對稱軸之一旋轉90度產生下一個正十二面體並與原有的正十二面體複合而成。在這個複合體當中8個頂點是原始立方體的頂點，另外24個頂點位於更大立方體的面上。

這個立體的複合方式與五角十二面體的二複合體相同，皆位於對偶位置。同時五角十二面體的二複合體也是黃鐵礦晶型的一種可能結構。

二複合五角十二面體：位於對偶位置的黃鐵礦晶體模型的木質模型

這種複合結構由24組多邊形組成，每組多邊形包含2個不等邊三角形和一個等腰三角形。其中不等邊三角形的一個邊長與等腰三角形的腰長相等，且其長度與二複合體對應的正十二面體邊長相等、第二條邊長為正十二面體邊長的一半、第三條邊長為：

長邊長度$=\frac{\sqrt{4+\sqrt{5}}}{2}a$

等腰三角形的底邊長為：

底邊長$=\frac{1+\sqrt{5}}{2}a=\phi a$

則其表面積$A$為：

$A=6\sqrt{2(5+\sqrt{5})}{a}^2\approx 22.8254a^2$

其中$a$為二複合體對應的正十二面體邊長、$\phi$為黃金比例。

完全扭稜立體

完全扭稜立體

原像	正四面體	立方體	正八面體	正十二面體	正二十面體
完全扭稜	完全扭稜四面體 β{3,3}	完全扭稜立方體 β{4,3}	二複合二十面體 β{3,4}	完全扭稜十二面體 β{5,3}	完全扭稜二十面體 β{3,5}

參見

• Template:Link-en