箕舌线

箕舌线是平面曲线的一种,也被稱為阿涅西的女巫(Template:Lang-en)[1][2][3]。
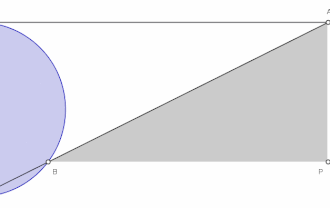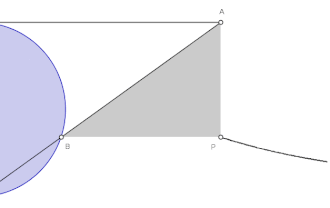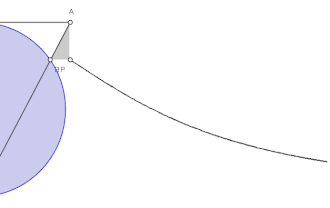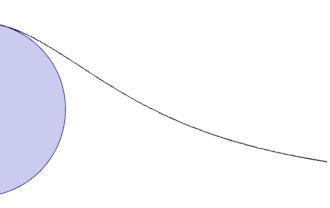
给定一个圆和圆上的一点O。对于圆上的任何其它点A,作割线OA。设M是O的对称点。OA与M的切线相交于N。过N且与OM平行的直线,与过A且与OM垂直的直线相交于P。则P的轨迹就是箕舌线。
箕舌线有一条渐近线,它是上述給定圓过O點的切线。
方程
设O是原点,M在正的y轴上。假设圆的半径是a。
则曲线的方程为 。
注意如果a=1/2,则曲线化为最简单的形式:
如果是OM与OA的夹角,则曲线的参数方程为:
如果是OA与x轴的夹角,则曲线的参数方程为:
性质

歷史
皮埃爾·德·費馬曾在1630年研究這條曲線。1703年時Template:Link-en提出了建構這條曲線的方法。1718年時格蘭迪建議將這條曲線命名為versoria,意思是張帆的繩子,並將這條曲線的義大利文名稱命名為versiera[4]
1748年時瑪利亞·阿涅西出版了著名的著作《Instituzioni analitiche ad uso della gioventù italiana》,其中箕舌线仍沿用格蘭迪取的名稱versiera[4],一恰好當時的義大利文Aversiera/Versiera是衍生自拉丁文的Adversarius,是魔鬼的一個稱呼「與神為敵的」,和女巫是同義詞[5]。也許因為這個原因,劍橋教授 Template:Link-en就誤譯了這條曲線。許多近代有關阿涅西及此曲線的著作對於誤譯的原因有些不同的猜測[6][7][8]Template:Link-en認為:
另一方面,史蒂芬·史蒂格勒認為是格蘭迪自己在玩文字遊戲[9]。
應用

箕舌线除了其理論的性質外.也常出現在現實生活中.不過這次應用是在20世紀末期及21世紀才有足夠的了解。在為一些物體現象建立數學模型時,會出現箕舌线[10]。 此方程式近似光线及X光的譜線分佈,也是共振電路中的能量耗散量。
光滑小山岳的截面也類似箕舌线。在數學建模中已用箕舌线作為一種流場的障礙物[11][12]。
参考文献
- ↑ 引用错误:
<ref>标签无效;未给name(名称)为(Emeritus)2000的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为Lienhard2002的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为MathWorld的ref(参考)提供文本 - ↑ 4.0 4.1 引用错误:
<ref>标签无效;未给name(名称)为truesdell的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-1的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-2的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-3的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-4的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-6的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-7的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-8的ref(参考)提供文本 - ↑ 引用错误:
<ref>标签无效;未给name(名称)为AutoSS-9的ref(参考)提供文本