S波

平面剪切波

二维网格中球面Template:Lang波的传播（经验模型）

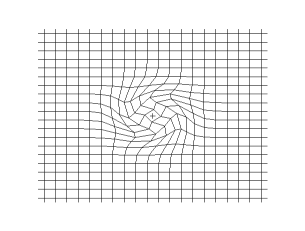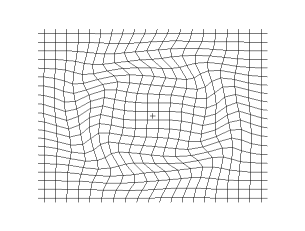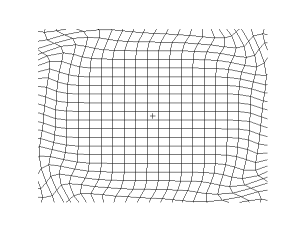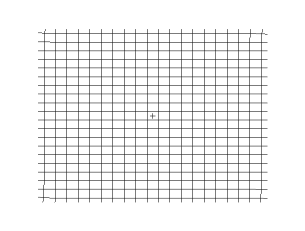
S波（Template:Lang，Template:Lang）是二種體波（體波的命名是因為此波穿越地球內部，相對於體波的是表面波）中之一。它是因地震而產生的，被地震儀記錄下來。命名為Template:Lang波（二次波，Template:Lang）是因為它的速度僅次於P波（最快的地震波）。Template:Lang波也可以代表剪切波（Template:Lang），因為Template:Lang波是一種橫波，地球內部粒子的震動方向與震波能量傳遞方向是垂直的。Template:Lang波與Template:LangP波不同的是，Template:Lang波無法穿越外地核。所以Template:Lang波的陰影區正對著地震的震源。

Template:Lang波移动时是剪切波或横波，因此其运动方向与波的传播方向是垂直的，若要形象地描述Template:Lang波，可以认为Template:Lang波是挥动绳子时，绳子上传播的波，这与P波是不同的。Template:Lang波是一种纵波，纵波就如振动的弹簧上传播的波，其形态就像蠕虫一样。Template:Lang波通过弹性介质移动，而主要的恢复力来自於剪切效应。这些波是不发散的，遵守不可压缩介质的连续性方程：

$\mathrm{\nabla }\cdot 𝐮=0$

原理

File:Earthquake wave shadow zone.svg

P波阴影区。S波不会穿过外核，因此在远离震中超过104°的全部区域S波都处在阴影区中（来源：USGS）

S波预测来自於1800年代的理论，最初来自於各向同性固体的應力－应变关系：

${\tau }_{ij}=\lambda {\delta }_{ij}{e}_{kk}+2\mu e_{ij}$

其中$\tau$是应力，$\lambda$和$\mu$是拉梅参数（$\mu$是剪切模量），${\delta }_{ij}$是克罗内克函数，而应变张量定义为

$e_{ij}=\frac{1}{2}({\partial }_i{u}_j+{\partial }_j{u}_i)$

其中u是应变位移。将後式代入前式得到

${\tau }_{ij}=\lambda {\delta }_{ij}{\partial }_k{u}_k+\mu ({\partial }_i{u}_j+{\partial }_j{u}_i)$

这种情况下的牛顿第二定律给出了地震波传播的运动齐次方程：

$\rho \frac{{\partial }^2{u}_i}{\partial t^2}={\partial }_j{\tau }_{ij}$

其中$\rho$是质量密度。代入上面的应力张量得到：

$\rho \frac{{\partial }^2{u}_i}{\partial t^2}={\partial }_i\lambda {\partial }_k{u}_k+{\partial }_j\mu ({\partial }_i{u}_j+{\partial }_j{u}_i)=\lambda {\partial }_i{\partial }_k{u}_k+\mu {\partial }_i{\partial }_j{u}_j+\mu {\partial }_j{\partial }_j{u}_i.$

利用向量恒等式并取一定的近似可得到均匀介质中的地震波方程：

$\rho \ddot{𝒖}=(\lambda +2\mu )\mathrm{\nabla }(\mathrm{\nabla }\cdot 𝒖)-\mu \mathrm{\nabla }\times (\mathrm{\nabla }\times 𝒖)$

其中Template:Link-en用於表示时间导数。取方程的旋度并利用向量恒等式最终得到：

${\mathrm{\nabla }}^2(\mathrm{\nabla }\times 𝒖)-\frac{1}{{\beta }^2}\frac{{\partial }^2(\mathrm{\nabla }\times 𝒖)}{\partial t^2}=0$

这一方程是一个只包含了u的旋度和速度$\beta$的波动方程，其中$\beta$满足

${\beta }^2=\frac{\mu }{\rho }$

这一公式描述了S波的传播。若用均匀介质中的地震波方程的散度代替旋度，则会得到描述P波传播的方程。

參見

• P波
• 橫波

参考文献

• Template:Cite book
• Template:Cite book
• Template:Cite book