考克斯特群

在數學中，考克斯特群是一類由空間中對超平面的鏡射生成的群。這類群廣泛出現於數學的各分支中，二面體群與正多胞體的對稱群都是例子；此外，根系對應到的外爾群也是考克斯特群。這類群以數學家哈羅德·斯科特·麥克唐納·考克斯特命名。

形式定義

所謂考克斯特群，是一個群 $W$ 寫成如下的表達式，即由滿足一些交互關係的生成元生成的群

$⟨r_1,r_2,\dots ,r_n\mid (r_i{r}_j{)}^{m_{ij}}=1⟩$

其中 $m_{ij}\in \mathbb{N}\cup \{\mathrm{\infty }\}$ 滿足 $m_{ii}=1$ 以及 $m_{ij}\ge 2$ 對所有 $i\ne j$。在此 $m_{ij}=\mathrm{\infty }$ 意指 $(r_i{r}_j{)}^m$ 恆不等於單位元。

注意到 $r_i^2=e$；若 $m_{ij}=2$，則 $r_i{r}_j=r_j{r}_i$。且 m 滿足對稱性 $m_{ij}=m_{ji}$。

令這組生成元為 $S$。資料 $(W,S)$ 稱為考克斯特群。方陣 $(m_{ij}{)}_{ij}$ 稱為考克斯特矩陣。

性質

有限考克斯特群的分類

設 $(W,S)$ 為考克斯特群，可證明存在一個有限維實矢量空間 $V$ 及其上的非退化雙線性形 $q$（未必正定），使得 $W$ 同構於正交群 $O(q)$ 的某個子群。由於 $S$ 的元素均為二階，可視之為 $(V,q)$ 中對某些超平面的鏡射。

利用 $(W,S)$ 的展示，定義元素的長度如下：對 $w\in W$，定義其長度 $\ell (w)$ 為所有表法 $w=r_{i_1}\cdots r_{i_s}(r_j\in S)$ 中最短的 $s$。由此可導出

$\mathrm{\forall }s\in S,\ell (ws)=\ell (w)\pm 1$

$\ell (w^{-1})=\ell (w)$

例子

• 對稱群 $S_n$ 是考克斯特群。在此可取 $S$ 為置換 $(1,2),(2,3),\dots ,(n-1,n)$；關係為 $((k,k+1)(k+1,k+2){)}^3=1$。

• 正多胞體的對稱：正多胞體的對稱群是有限考克斯特群。舉例明之：正多邊形的對稱群是二面體群，正 n 維單形的對稱群是前述的 $S_{n+1}$，又稱為 $A_n$ 型的考克斯特群。n 維超正方體的對稱群為 $B{C}_n$。正十二面體與正二十面體的對稱群是 $H_3$。在四維空間中，存在三種特別的正多胞體──正二十四胞體、正一百二十胞體與正六百胞體，其對稱群分別是 $F_4,H_4,H_4$。$D_n,E_6,E_7,E_8$ 可以由某些半正多胞體的對稱群得到。

• 外爾群：每個根系的外爾群都是有限考克斯特群。

• 仿射外爾群：仿射外爾群是無限群，但帶有一個正則阿貝爾子群，使得對應的商群是個外爾群。

分類

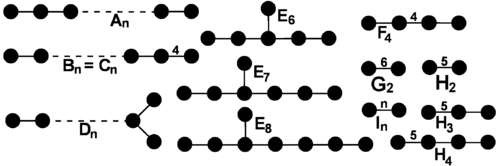
一般而言，兩個群展示的同構與否是無法判定的。然而對考克斯特群則有一個簡單的判準，稱為交換條件。可以透過考克斯特-丹金圖分類有限考克斯特群。圖的構造方式為：

1. 每個生成元對應到一個頂點。
2. 若 $m_{ij}\ge 3$，則頂點 $r_i,r_j$ 之間有邊相連。
3. 若 $m_{ij}\ge 4$，則將邊標上 $m_{ij}$。

文獻

• Larry C Grove and Clark T. Benson, Finite Reflection Groups (1985), Graduate texts in mathematics, vol. 99, Springer.
• Paul Garrett, Buildings and Classical Groups (1997), Chapman Hall. ISBN 0-412-06331-X . PostScript 檔案下載 Template:Wayback .
• James E. Humphreys, Reflection Groups and Coxeter Groups (1990), Cambridge studies in advanced mathematics, 29.