環帶多面體

Template:Expert Template:NoteTA 環帶多面體 （全對稱多面體）是一種每個面都相對稱、相等或與正對的（即將兩個面的中心連起可過內接球或外接球球心）面互相對稱的立體。

環帶多面體對於空間的填充

另外，某些卡塔蘭立體（半正多面體的對偶多面體）也同樣是環帶多面體：

其他有菱形面的環帶多面體：

名稱(環帶多面體)	對稱群	正多邊形面	面的可遞性	邊的可遞性	頂點的可遞性	空間填充(space filling)	Number of generators
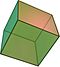
正方體 4.4.4	Oh群	有	有	有	有	有	3
六角柱 4.4.6	D6h群	有	無	無	有	有	4
稜柱 4.4.2n $(n > 3)$	Dnh群	有	無	無	有	無	n+1
截角八面體 4.6.6	Oh群	有	無	無	有	有
大斜方截半立方體 4.6.8	Oh群	有	無	無	有	無
大斜方截半二十面體 4.6.10	Ih群	有	無	無	有	無
菱形十二面體 V3.4.3.4	Oh群	無	有	有	無	有
菱形三十面體 V3.5.3.5	Ih群	無	有	有	無	無	6
菱形六角化十二面體	D4h群	無	無	無	無	有	5
截角菱形十二面體	Oh群	無	無	無	無	無