正弦定理

Template:三角学 正弦定理是三角学中的一个定理。它指出：对于任意$\mathrm{△}ABC$，$a$、$b$、$c$分别为$\mathrm{\angle }A$、$\mathrm{\angle }B$、$\mathrm{\angle }C$的对边，$R$为$\mathrm{△}ABC$的外接圆半径，则有

$\frac{a}{\sin \mathrm{\angle }A}=\frac{b}{\sin \mathrm{\angle }B}=\frac{c}{\sin \mathrm{\angle }C}=2R$

證明

法一

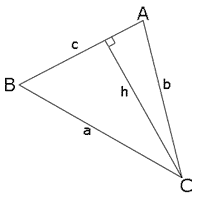
做一个边长为$a$，$b$，$c$的三角形，对应角分别是$A$，$B$，$C$。从角$C$向$c$边做垂线，得到一个长度为h的垂线和两个直角三角形。

显然：

$\sin A=\frac{h}{b}$

且:

$\sin B=\frac{h}{a}$

故：

$h=b\sin A=a\sin B$

故:

$\frac{\sin A}{a}=\frac{\sin B}{b}$

同理可證：

$\frac{\sin B}{b}=\frac{\sin C}{c}$

法二

作$\mathrm{△}ABC$的外接圆，设半径为$R$，$BC=a$

角A为锐角时

由于$\mathrm{\angle }A$与$\mathrm{\angle }D$所对的弧都为$BC$，根据圆周角定理可瞭解到

$\mathrm{\angle }\mathrm{A}\mathrm{=}\mathrm{\angle }\mathrm{D}$

由于$BD$为外接圆直径，

$\mathrm{B}\mathrm{D}=2R,\mathrm{\angle }\mathrm{B}\mathrm{C}\mathrm{D}=\frac{\pi }{2}rad$

所以

$\sin \mathrm{\angle }D=\frac{a}{2R}$

$\sin \mathrm{\angle }A=\frac{a}{2R}$

$\frac{a}{\sin \mathrm{\angle }A}=2R$

角A为直角时

因为$BC=a=2R$，可以得到

$\sin \mathrm{\angle }A=\sin \frac{\pi }{2}=1$

所以可以证明

$\frac{a}{\sin \mathrm{\angle }A}=2R$

角A为钝角时

线段$BD$是圆的直径 根据圆内接四边形对角互补的性质

$\mathrm{\angle }\mathrm{D}\mathrm{=}\mathrm{\pi }\mathrm{-}\mathrm{\angle }\mathrm{B}\mathrm{A}\mathrm{C}$

所以

$\sin \mathrm{\angle }BAC=\sin \mathrm{\angle }D$

因为$BD$为外接圆的直径$BD=2R$。根据正弦定义

$\sin \mathrm{\angle }BAC=\sin \mathrm{\angle }D=\frac{a}{2R}$

变形可得

$\frac{a}{\sin \mathrm{\angle }BAC}=2R$

根据以上的证明方法可以证明得到得到三角形的一条边与其对角的正弦值的比等于外接圆的直径，即

$\frac{a}{\sin \mathrm{\angle }A}=\frac{b}{\sin \mathrm{\angle }B}=\frac{c}{\sin \mathrm{\angle }C}=2R$

运用

三面角正弦定理

若三面角的三个面角分别为$\alpha$、$\beta$、$\gamma$，它们所对的二面角分别为$A$、$B$、$C$，则

$\frac{\sin \alpha }{\sin A}=\frac{\sin \beta }{\sin B}=\frac{\sin \gamma }{\sin C}$

多边形的正弦关系

$\frac{OA}{\sin \mathrm{\angle }OBA}=\frac{OB}{\sin \mathrm{\angle }OAB},\frac{OB}{\sin \mathrm{\angle }OCB}=\frac{OC}{\sin \mathrm{\angle }OBC},\frac{OC}{\sin \mathrm{\angle }ODC}=\frac{OD}{\sin \mathrm{\angle }OCD},\frac{OD}{\sin \mathrm{\angle }OED}=\frac{OE}{\sin \mathrm{\angle }ODE},\frac{OE}{\sin \mathrm{\angle }OAE}=\frac{OA}{\sin \mathrm{\angle }OEA}$

$\frac{\sin \mathrm{\angle }OAB\sin \mathrm{\angle }OBC\sin \mathrm{\angle }OCD\sin \mathrm{\angle }ODE\sin \mathrm{\angle }OEA}{\sin \mathrm{\angle }OBA\sin \mathrm{\angle }OCB\sin \mathrm{\angle }ODC\sin \mathrm{\angle }OED\sin \mathrm{\angle }OAE}=\frac{OB\cdot OC\cdot OD\cdot OE\cdot OA}{OA\cdot OB\cdot OC\cdot OD\cdot OE}=1$

$\sin \mathrm{\angle }OAB\sin \mathrm{\angle }OBC\sin \mathrm{\angle }OCD\sin \mathrm{\angle }ODE\sin \mathrm{\angle }OEA=\sin \mathrm{\angle }OBA\sin \mathrm{\angle }OCB\sin \mathrm{\angle }ODC\sin \mathrm{\angle }OED\sin \mathrm{\angle }OAE$

外部链接

• 关于K级顶点角的正弦定理及应用 Template:Wayback
• 关于正弦定理在四面体中的类比定理 Template:Wayback
• 正弦定理证明 Template:Wayback

參阅

• 余弦定理
• 正切定理
• 角平分線長公式
• 中線長公式