截半正七邊形鑲嵌

Template:NoteTA Template:Infobox polyhedron 在幾何學中，截半正七邊形鑲嵌（Template:Lang-en）是一種由正七邊形與正三角形拼合，並且將正七邊形重複排列組合，並讓圖形完全拼合，而且沒有空隙或重疊的幾何構造。其為正七邊形鑲嵌經截半變換後的像，是一種雙曲半正鑲嵌，每個頂點皆由兩個正七邊形與兩個正三角形構成。在施萊夫利符號中用r{7,3}表示；此外其邊緣形成一個無限排列的雙曲面直線，此性質與截半正六邊形鑲嵌相似。

截半正七邊形鑲嵌無法在一個平面上構造，因為每個頂點的角度$128{\frac{4}{7}}^{\circ }\times 2+60^{\circ }\times 2=377{\frac{1}{7}}^{\circ }$超過了360度，但若硬將正七邊形與正三角形邊對邊接合，將會變成一個馬鞍形，且每個頂點皆會落在一個雙曲拋物面上，雖然它不能在歐幾里得平面上構造，但可以在一個雙曲拋物面上構造，因此截半正七邊形鑲嵌也是羅氏幾何或雙曲幾何中討論的幾何構造。

圖片

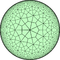
克萊因圓盤模型保留了直線，但是扭曲了角度

截半正七邊形鑲嵌的對偶鑲嵌稱為七階三菱形鑲嵌（Template:Lang-en），由七個和三個菱形交錯的頂點組成。

相關半正鑲嵌

截半正七邊形鑲嵌在拓撲上與一系列一直延伸到雙曲鑲嵌的頂點圖為3.n.3.n的（廣義）擬正多面體相關：

擬正多面體和鑲嵌系列：3.n.3.n

對稱性 *n32 [n,3]	球面			歐氏鑲嵌	緊湊型雙曲鑲嵌		仿緊型鑲嵌	非緊型鑲嵌
	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] p6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[iπ/λ,3]
擬正頂點 布局	3.3.3.3	3.4.3.4	3.5.3.5	3.6.3.6	3.7.3.7	3.8.3.8	3.∞.3.∞	Template:AnyLink
考克斯特紀號	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD
對偶 (菱形) 頂點 布局	V3.3.3.3	V3.4.3.4	V3.5.3.5	V3.6.3.6	V3.7.3.7	V3.8.3.8	V3.∞.3.∞
考克斯特紀號	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD

從Template:En-link中可得到8種不同的半正鑲嵌

半正七邊形/三角形鑲嵌

對稱群：[7,3], (*732)							[7,3]+, (732)
Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD
{7,3}	t{7,3}	r{7,3}	2t{7,3}=t{3,7}	2r{7,3}={3,7}	rr{7,3}	tr{7,3}	sr{7,3}
半正對偶
Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

擬正多面體和鑲嵌系列：7.n.7.n

對稱群 *7n2 [n,7]	雙曲鑲嵌						仿緊湊	非緊湊
	*732 [3,7]	*742 [4,7]	*752 [5,7]	*762 [6,7]	*772 [7,7]	*872 [8,7]...	*∞72 [∞,7]	[iπ/λ,7]
考克斯特紀號	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD	Template:CDD
擬正 頂點 布局	3.7.3.7	4.7.4.7	7.5.7.5	7.6.7.6	7.7.7.7	7.8.7.8	7.∞.7.∞	Template:AnyLink

參見

• 截半正六邊形鑲嵌 - 3.6.3.6 鑲嵌
  • 菱形鑲嵌 - V3.6.3.6 鑲嵌的對偶
• 正多邊形鑲嵌
• 半正鑲嵌列表

參考文獻

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• Template:Cite book
• Template:MathWorld
• Template:MathWorld
• Hyperbolic and Spherical Tiling Gallery Template:Wayback
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings Template:Wayback
• Hyperbolic Planar Tessellations, Don Hatch Template:Wayback