二十四胞體
Template:NoteTA Template:Geometric Shape Example 在幾何學中,二十四胞體是指有24個胞或維面的多胞體[1]。所有四維或四維以上空間中的二十四胞體共有3個正圖形,也就是說有3種正二十四胞體,分別位於四維空間、十二維空間和23維空間,其中四維空間的正二十四胞體稱為四維正二十四胞體,由24個正八面體所組成,另兩個分別是十二維空間的立方形和23維空間的單純形。
四維二十四胞體
在四維空間中,二十四胞體為由24個多面體所組成的多胞體,四維空間中唯一具有24個胞的正圖形是由24個正八面體所組成的二十四胞體稱為正二十四胞體。此外亦存在許多半正的二十四胞體,例如截角超立方體、截角十六胞體等[2]。
| 名稱 | 考克斯特 施萊夫利 |
胞 | 圖像 | 展開圖 |
|---|---|---|---|---|
| 正二十四胞體[3] | Template:CDD Template:CDD Template:CDD Template:CDDTemplate:CDD {3,4,3}[4] r{3,3,4} = {31,1,1} = |
24個正八面體 |
 |
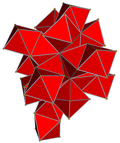 [5] [5]
|
| 截角超立方體 | Template:CDD t{4,3,3} |
8個截角立方體 16個正四面體 |
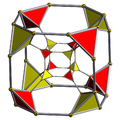 |

|
| 截半超立方體[6][7] | Template:CDD Template:CDD Template:CDD = Template:CDD r{4,3,3} = 2r{3,31,1} h3{4,3,3} |
8個截半立方體 16個正四面體 |
 |
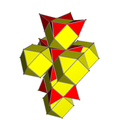
|
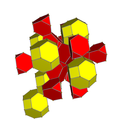
| 過截角超立方體 過截角十六胞體 |
Template:CDD Template:CDD Template:CDD = Template:CDD 2t{4,3,3} 2t{3,31,1} h2,3{4,3,3} |
8個截角八面體 16個截角四面體 |
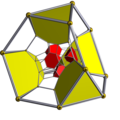 |
|
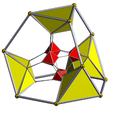
| 截角十六胞體 | Template:CDD Template:CDD Template:CDD = Template:CDD t{4,3,3} t{3,31,1} h2{4,3,3} |
8個正八面體 16個截角四面體 |
 |

|
五維二十四胞體
在五維空間中,二十四胞體為由24個四維多胞體所組成的幾何形狀,但當中不包括任何正圖形、辦正圖形或均勻多胞體。
二十三維正二十四胞體

在二十三維空間幾何學中,正二十四胞體是23維空間的一種自身對偶的正多胞體,由24個22維單純形組成,是一個23維空間中的單純形。
二十三維正二十四胞體位於其皮特里多邊形的正交投影是一個24個頂點的完全圖。二十三維正二十四胞體的皮特里多邊形是一個扭歪二十四邊形,其具有A23的考克斯特群的對稱性[8]。
參見
參考文獻
- ↑ Johnson (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups
- ↑ Template:KlitzingPolytopes, (x3x3o4o - thex)
- ↑ Matila Ghyka, The Geometry of Art and Life (1977), p.68
- ↑ Template:Cite mathworld
- ↑ Buekenhout, F. and Parker, M. "The Number of Nets of the Regular Convex Polytopes in Dimension <=4." Disc. Math. 186, 69-94, 1998.
- ↑ Template:PolyCell
- ↑ Template:KlitzingPolytopes
- ↑ Template:Citation