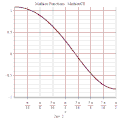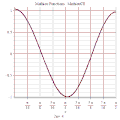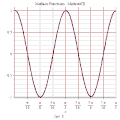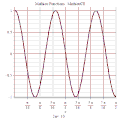
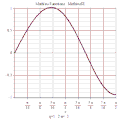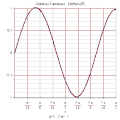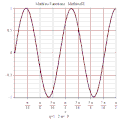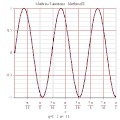
MathieuCE 3D
MathieuCE 3D
 MathieuSE 3D
MathieuSE 3D
马丟函数(Template:Lang-fr)是1868年法國數學家Template:Tsl因研究数学物理所推得的特殊函數,下列马丟方程的解析解:
马丟方程有两个线性无关的解:
- 奇数解
MathieuCE(n, q, x),或记为,
- 偶数解
MathieuSE(n, q, x).或记为
称为基本解[1]
周期性
马丟函数 MathieuC(a,q,z) 或 MathieuS(a,q,z) 只有一个是周期为 或的周期解,另一个不是。
马丟函数 MathieuC(a,q,z) 和 MathieuS(a,q,z) 两者都有是周期为(n≥2)的周期函数。
[1]
正交性
特征方程
 Mathieu Eigen value a(n,q)
Mathieu Eigen value a(n,q)
 Mathieu eigenvalue b(n,q)
Mathieu eigenvalue b(n,q)
马丟方程的特征方程是[1]
对于给定的v,q, 上列特征方程给出无穷多个a、b解称为特征值。
特征值的展开
马丟函数体特征值可展开成级数:[2]
级数展开
马丟函数ce,se的级数展开[3]
傅立叶展开式
马丟函数的傅立叶展开:[3]
其中系数A,B满足下列递归关系:[3]
关系式
马丟方程的基本解满足下列关系:[3]:
- =
郎斯基行列式:
特例
夫洛开解
 Mathieu Floquet
Mathieu Floquet
马丟函数中,如果 是一个周期为的解,并满足下列条件
,其中与x 无关,则此解称为夫洛开解。
- 级数展开
参考文献
- ↑ 1.0 1.1 1.2 王竹溪 郭敦仁 603 引用错误:
<ref>标签无效;同一name(名称)“W”以不同内容定义了多次
- ↑ Frank p659
- ↑ 3.0 3.1 3.2 3.3 Frank p660 引用错误:
<ref>标签无效;同一name(名称)“F”以不同内容定义了多次
- 王竹溪 郭敦仁 《特殊函数概论》 第十二章 马丟函数 北京大学出版社 2000
- Frank J Oliver NIST Handbook of Mathematical Functions,Cambridge University PRESS, 2010