電荷泵鎖相迴路

電荷泵鎖相迴路

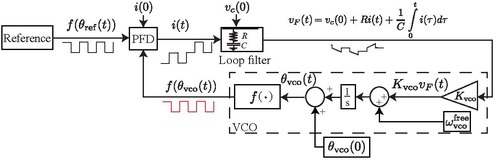
電荷泵鎖相迴路（Charge-pump phase-locked loop）簡稱CP-PLL，是一種鉴相器適用於方波輸入信號的鎖相迴路。CP-PLL可以快速的鎖定到輸入信號的相位，可以達到很低的穩態相位誤差。

鉴相器（PFD）

鉴相器動態

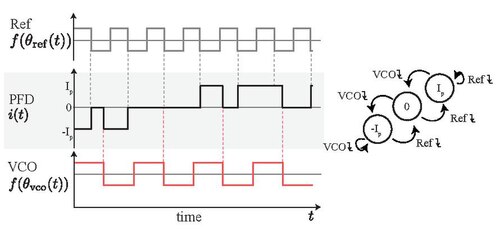
鉴相器（PFD）是由參考信號（Ref）以及受控輸出（VCO）信號的下緣所觸發。PFD $i(t)$的輸出信號只有三個狀態：0, $+I_p$,和$-I_p$。 參考信號的下緣會使PFD切換到較高的狀態，若PFD已經在$+I_p$就不會變動。 VCO信號的下緣會使PFD切換到較低的狀態，若PFD已經在$-I_p$就不會變動。 若二個信號的下緣同時出現，PFD會切換到0。

CP-PLL的數學模型

第一個二階CP-PLL的數學模型是由Template:Le在1980年提出的。M. van Paemel在1994年提出了不考慮VCO過載（overload）的非線性模型，N. Kuznetsov等人在2019年優化該模型。也有學者在推導考慮VCO過載的CP-PLL解析解數學模型。

CP-PLL的數學模型可以針對一些參數進行解析的預估，例如hold-in範圍（在VCO沒有過載的情形下，可能進行鎖相的輸入信號頻率範圍），及捕獲範圍（pull-in range，在CP-PLL任意初始狀態下，CP-PLL最終可以鎖相的輸入信號頻率範圍）。

二階CP-PLL的連續時間線性模型以及加德納的猜想

加德納的分析是以以下的近似為基礎：每個參考信號的周期內，PFD非零的時間區間為

$t_p=|{\theta }_e|/{\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}},{\theta }_e={\theta }_{\mathrm{r}\mathrm{e}\mathrm{f}}-{\theta }_{\mathrm{v}\mathrm{c}\mathrm{o}}.$

CP-PLL的PDF平均輸出為

$i_d=I_p{\theta }_e/2\pi$

對應的傳遞函數為

$I_d(s)=I_p{\theta }_e(s)/2\pi$

若用濾波器傳遞函數$F(s)=R+\frac{1}{Cs}$以及VCO傳遞函數${\theta }_{\mathrm{v}\mathrm{c}\mathrm{o}}(s)=K_{\mathrm{v}\mathrm{c}\mathrm{o}}{I}_d(s)F(s)/s$，可以得到加德納的二階CP-PLL線性近似平均模型:

$\frac{{\theta }_e(s)}{{\theta }_{\mathrm{r}\mathrm{e}\mathrm{f}}(s)}=\frac{2\pi s}{2\pi s+K_{\mathrm{v}\mathrm{c}\mathrm{o}}{I}_p(R+\frac{1}{Cs})}.$

Template:Le在1980年以上述的理解，提出了猜想：「實際電荷泵鎖相迴路的暫態響應，預期會和等效傳統PLL的暫態響應幾乎相同。」Template:Rp（加德納對CP-PLL的猜想）。 依照加德納的結果，也類似Egan在type 2 APLL捕獲範圍的猜想，Amr M. Fahim在其書中猜想Template:Rp：為了要達到無限大的捕獲範圍，CP-PLL的迴路濾波器需要使用主動濾波器（Fahim-Egan在type II CP-PLL捕獲範圍的猜想）。

二階CP-PLL的連續時間非線性模型

為了簡化推導，但不失去通用性，假設VCO和參考信號在其相位為整數時為其下降緣。 令參考信號第一個下降緣的時間為$t=0$。 PFD狀態$i(0)$會依PFD的初始狀態$i(0-)$，VCO的初始相位移${\theta }_{vco}(0)$，以及參考信號${\theta }_{ref}(0)$的值而不同。

若利用電阻和電容製作純PI（比例積分）的濾波器，其輸入電流$i(t)$和輸出電壓$v_F(t)$的關係為

$\begin{array}{c}{v}_F(t)=v_c(0)+Ri(t)+\frac{1}{C}\underset{0}{\overset{t}{\int }}i(\tau )d\tau \end{array}$

其中$R>0$是電阻，$C>0$是電感。 $v_c(t)$是電容器的電壓。 控制信號$v_F(t)$會調整VCO頻率：

$\begin{array}{c}{\dot{\theta }}_{vco}(t)={\omega }_{vco}(t)={\omega }_{vco}^{\text{free}}+K_{vco}{v}_F(t),\end{array}$

其中${\omega }_{vco}^{\text{free}}$是VCO的自由運行頻率 （也就是$v_F(t)\equiv 0$)，$K_{vco}$是VCO增益（靈敏度）、${\theta }_{vco}(t)$是VCO相位。 最後，CP-PLL連續時間非線性數學模型如下

$\begin{array}{c}{\dot{v}}_c(t)=\frac{1}{C}i(t),{\dot{\theta }}_{vco}(t)={\omega }_{vco}^{\text{free}}+K_{vco}(Ri(t)+v_c(t))\end{array}$

其中有以下的不連續分段常數非線性

$i(t)=i(i(t-),{\theta }_{ref}(t),{\theta }_{vco}(t))$

初始條件為$(v_c(0),{\theta }_{vco}(0))$. 此模型是非線性、非自主式、不連續的開關系統。

二階CP-PLL的離散時間非線性模型

在時間區間內的PFD動態

假設參考信號頻率為常數: ${\theta }_{ref}(t)={\omega }_{ref}t=\frac{t}{T_{ref}},$ 其中$T_{ref}$、${\omega }_{ref}$和${\theta }_{ref}(t)$是參考資料的週期、頻率和相位。

令$t_0=0$， 這表示$t_0^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}$是第一個PFD輸出為0的時間 （若$i(0)=0$，則$t_0^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}=0$） 且$t_1$是VCO或參考信號的第一個下降緣。 其且，可以定義對應的遞減數列$\{t_k\}$、$\{t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}\}$，其中$k=0,1,2...$。

令$t_k<t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}$. 則在$t\in [t_k,t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}})$時，$\text{sign}(i(t))$是非零的常數（$\pm 1$）。 令${\tau }_k$為PFD脈波寬度（PFD輸出為非零長度的時間區間）乘以PFD輸出的正負號：

${\tau }_k=(t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}-t_k)\text{sign}(i(t))$ for $t\in [t_k,t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}})$

${\tau }_k=0$ for $t_k=t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}}$

若VCO的下降緣在參考信號的下降緣之前，則${\tau }_k<0$，反之，可得${\tau }_k>0$。${\tau }_k$可以看出二個信號下降緣的先後順序。在$(t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}},t_{k+1})$區間內，PFD輸出為零，PFD $i(t)\equiv 0$：

$v_F(t)\equiv v_k$ for $t\in [t_k^{\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{l}\mathrm{e}},t_{k+1})$.

將$({\tau }_k,v_k)$變成下式的變數變換 $p_k=\frac{{\tau }_k}{T_{\mathrm{r}\mathrm{e}\mathrm{f}}},u_k=T_{\mathrm{r}\mathrm{e}\mathrm{f}}({\omega }_{\mathrm{v}\mathrm{c}\mathrm{o}}^{\text{free}}+K_{\mathrm{v}\mathrm{c}\mathrm{o}}{v}_k)-1,$ 可以讓參數減至二個： $\alpha =K_{\mathrm{v}\mathrm{c}\mathrm{o}}{I}_p{T}_{\mathrm{r}\mathrm{e}\mathrm{f}}R,\beta =\frac{K_{\mathrm{v}\mathrm{c}\mathrm{o}}{I}_p{T}_{\mathrm{r}\mathrm{e}\mathrm{f}}^2}{2C}.$

此處$p_k$是正規化的相位偏移，$u_k+1$是VCO頻率 ${\omega }_{\mathrm{v}\mathrm{c}\mathrm{o}}^{\text{free}}+K_{\mathrm{v}\mathrm{c}\mathrm{o}}{v}_k$相對於參考頻率$\frac{1}{T_{\mathrm{r}\mathrm{e}\mathrm{f}}}$的比例。

最後，不考慮VCO過載的二階CP-PLL離散時間模型如下

$\begin{array}{cc}& u_{k+1}=u_k+2\beta p_{k+1},\\ & p_{k+1}=\{\begin{array}{c}\frac{-(u_k+\alpha +1)+\sqrt{(u_k+\alpha +1{)}^2-4\beta c_k}}{2\beta },\text{ for }{p}_k\ge 0,c_k\le 0,\\ \frac{1}{u_k+1}-1+(p_k\text{ mod }1),\text{ for }{p}_k\ge 0,c_k>0,\\ l_k-1,\text{ for }{p}_k<0,l_k\le 1,\\ \frac{-(u_k+\alpha +1)+\sqrt{(u_k+\alpha +1{)}^2-4\beta d_k}}{2\beta },\text{ for }{p}_k<0,l_k>1,\end{array}\end{array}$

其中

$\begin{array}{c}{c}_k=(1-(p_k\text{ mod }1))(u_k+1)-1,S_{l_k}=-(u_k-\alpha +1)p_k+\beta p_k^2,l_k=\frac{1-(S_{l_k}\text{ mod }1)}{u_k+1},d_k=(S_{l_k}\text{ mod }1)+u_k.\end{array}$

此離散時間模型只在$(u_k=0,p_k=0)$有一個穩態，可以估計hold-in範圍和捕獲範圍。

若VCO過載，也就是${\dot{\theta }}_{\mathrm{v}\mathrm{c}\mathrm{o}}(t)$為零， 或者是以下的式子 $(p_k>0,u_k<2\beta p_k-1)$或 $(p_k<0,u_k<\alpha -1)$, 則需要考慮額外的CP-PLL動態特性。 針對任何參數，只要VCO和參考信號的頻率差夠大，就會使VCO過載。 在實務上，需避免VCO的過載。

高階CP-PLL的非線性模型

高階CP-PLL非線性模型推導和超越方程有關，無法求得解析解，需要用近似的方式計算